航班超售与舱位控制综合优化

乐美龙，张健泽

(上海海事大学a.科学研究院;b.物流研究中心，上海201306)

0 引言

航空收益管理是航空公司进行定量化管理提高收益的重要手段，多年来国外已经有了许多深入的研究［1－2］，其主要包括超售、舱位控制、动态定价等方面。超售指可预订座位量超过飞机的实际容量，用于控制航班空位现象的发生。国外对于超售的研究较早，1985 年，文献［3］提出了一个单票价静态超售模型，考虑空位与拒载成本之间的平衡关系来求解超售数量;1995 年，文献［4］提出了多票价等级静态超售模型，采用近似替代方法进行求解;1999 年，文献［5］将预订请求的到达假设为齐次泊松过程，运用Bellman-Jacobi 方程对模型进行分析，并求解了分段超售限制的最优解;文献［6］假设一个时间段内只允许预订或取消事件发生，提出了一般性情况下的多票价等级超售模型;2004 年，文献［7］考虑在座位等级可替代情况下研究超售问题，证明此方法可有效降低拒载人数;2011 年，文献［8］在需求和到达率不确定下建立静态超售模型，并分析了超售水平与航空公司服务质量之间的关系。

舱位控制是航空收益管理的核心问题，较为著名的研究是Belobaba 于1987 年提出的EMSRa 模型［9］，用于计算多舱位等级的预订限制和保护水平;后来又提出了更加符合实际的EMSRb 模型［10］。2006 年，文献［11］对舱位控制问题进行了较为系统的研究，考虑了竞争环境、批量订购及多航段等情况下的舱位控制。

在以上研究中，多数将舱位控制与超售分开讨论，因问题的复杂性，两者综合起来进行研究存在较大的困难，在静态建模方面，2006 年，文献［12］研究了多等级超售与舱位静态控制问题;文献［13］将订座过程假设为排队系统进行研究;2010 年，文献［14］建立静态模型求解超售策略下的舱位控制问题，并运用Jensen 不等式将模型转化成线性规划问题进行近似求解。动态建模方面，2007 年文献［15］运用马尔科夫过程建立动态超售模型，假设了航班舱位开放的先后次序，在串行控制和并行控制下求解得到单等级和多等级的座位分配数量。

1 模型建立

模型假设每一个预订或取消行为独立发生，乘客在飞机起飞之前取消预订的平均退款为κ，Noshow 情况下则不给予退款。为便于建模，本文中航班乘客的到达率与取消率均与舱位等级无关，用平均到达率βs与平均取消率βc来表示。另外，当到达乘客数量大于飞机实际容量时，有一部分乘客不得不被拒载，航空公司要为此支付赔偿，拒载成本与票价无关，这与实际情况相符合。

本文使用的符号如下所示:m 为航班的舱位等级总数;Di为i 舱位等级的需求数量，i =1，…，m;C为飞机座位容量;n 为售票过程中的座位预订数量;bi为i 舱位等级的预订限制，i=1，…，m;ri为i 舱位等级的票价;βs为航班乘客平均到达率;βc为航班乘客平均取消预订的概率;κ 为航班乘客取消预订的平均退款;θ 为每一位被拒载乘客所获得的补偿成本，与舱位等级i 无关。

根据以上假设及描述建立离散时间动态模型，由于每一个预订请求的到达是随机的，各舱位等级之间的预订请求，通过设置一定的参数来模拟实际到达的先后顺序。在某一时间点当预订请求到达时，系统决定接受还是拒绝该预订请求，确定航班的座位分配方案，以达到期望总收益的最大化。

图1 为动态订座过程，图1 中，0 代表机票开始预订时刻;T 表示航班起飞时刻，预订请求及取消请求在离散时间点tk=kh，k =1，…，K－1 发生，并且两者相互独立，T=Kh，t0=0，在时间段区间Ik=［tk－1，tk)内至多只有一个请求。

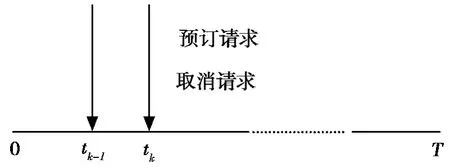
图1 动态订座过程

对于取消请求过程，由于每一个取消请求都是独立的，假设区间Ik取消的概率是c(Ik)，k =2，…，K，在时刻tk－1，已接受的预订请求数量为n，那么在时间段Ik取消的人数服从二项分布B(c(Ik)，n)，在时刻tk之前，接受的预订请求数量服从B(1－c(Ik)，n)，当c(Ik)=1－exp(－λch)，取消过程可以用参数为λc的齐次马尔科夫生灭过程来表示，此时取消概率并不依赖于预订数量，称该性质为“无记忆性”。

另外，假设在时间点tk舱位等级i 预订请求到达的概率为pi(tk)，用r0=0 表示乘客到达却没有购买机票的情况，不失一般性，假设r0＜r1＜…＜rm，每一个取消预订请求获得固定的退款为κ，对于拒载的乘客赔付的补偿为θ。

改善灌溉质量，优化水源布局。项目区农田集中连片，田间输水大面积实现管道化，不仅使灌溉保证率大大提高，灌溉质量大为改善，也使亩均灌溉定额降低到110m3左右，节水率高达60%以上。通过实施高标准节水灌溉工程，进一步优化了水源布局，把原有井控面积从70～80亩提高到现在的160～300亩，将过去井群密集、出水量小、能耗高、控制面积小的机电井彻底压减封闭，做到了真压井、压真井。两年来，全市累计压减机电井1.3万眼，节约水资源3.1亿m3，农业用水比例由原来的85%下降到80%。

为便于说明，假设t+k表示在区间Ik内预订请求到达时，采取接受还是拒绝的决策时间点，k =1，…，K－1，预订数量为n 时，令Jk(n)，k=1，…，K－1 表示从时间点t+k到t+K的期望收益，在时间点t+k有n 个已接受的预订请求之后，在区间Ik+1内取消预订的数量服从二项分布B(c(Ik+1)，n)。因此，在时刻tk+1前的总预订数量为B(1－c(Ik+1)，n)，那么在航班起飞时刻的总预订数量服从B(1－c(IK)，n)，到达的乘客总数服从B(βs(1－c(IK))，n)，并且E(B(c(Ik+1)，n))=nc(Ik)。根据以上假设及描述，建立动态规划模型PDP:

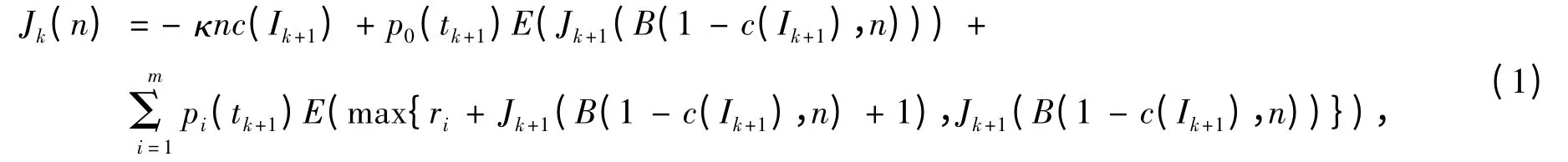
其边界条件为:

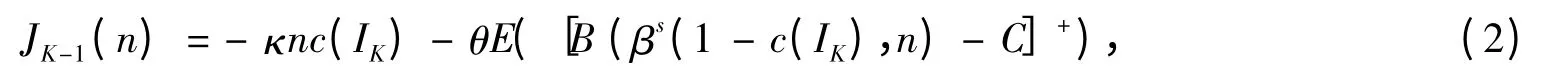
当n=0 时，有P(B(1－c(Ik+1)，0)=0)=1，因此，式(1)的初始边界条件为:

式(1)中第1 项表示在k+1 时刻取消预订的退款;第2 项表示在k+1 时刻乘客到达但没有预订机票的情况下，维持原系统预订人数下的期望收益;第3 项表示在不同舱位等级的预订请求发生时系统的期望收入;式(2)第2 项中，E(［B(βs(1－c(IK)，n)－C］+)表示在飞机起飞时刻，由于超售所造成的期望拒载人数;式(3)表示当系统中第一个请求到达时的初始条件。

为求解该模型，对模型的性质进行如下分析:

定理1 假设r ＞0，当函数f 是离散上凸函数，那么函数h(n):h(n)=max{r+f(n+1)，f(n)}也是离散上凸函数。

限于篇幅，证明从略。

证明 由二项分布的性质可知:二项分布B(p，n)可分解成n 个独立0－1 分布之和，因此，二项分布B(p，n)可分解为:

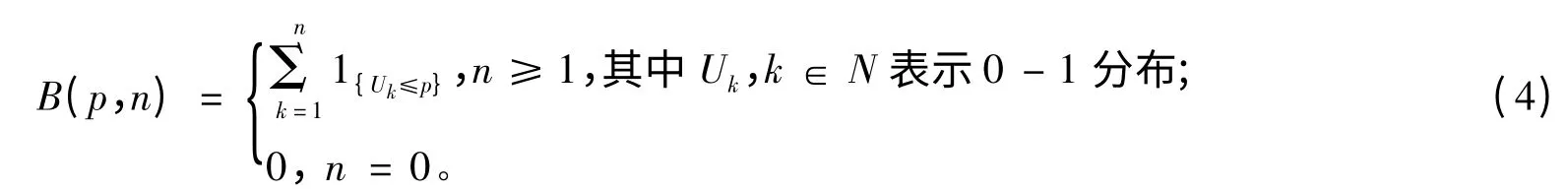
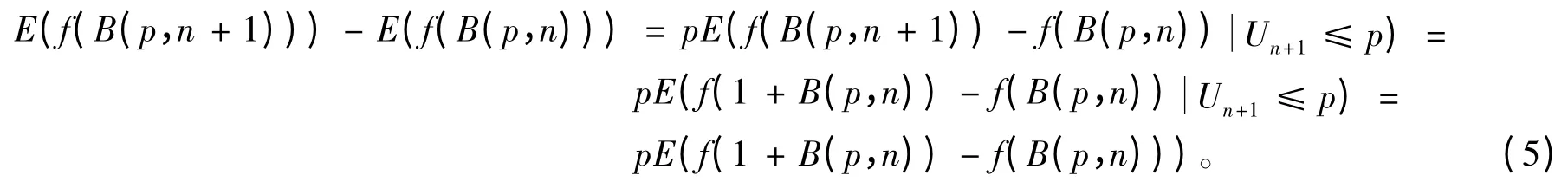
证毕。

定理3 对于k=1，…，K－1，函数Jk(n)是关于n 的离散上凸函数。

证明 引入函数

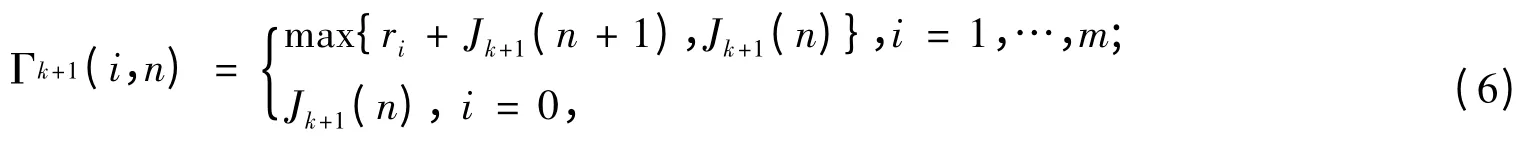
则PDP可变换为:

证毕。

在实际中，对于求解的每一个舱位等级的独立座位数量意义不大，因为航空公司通常会采取嵌套策略，即当高票价的座位数量售完，低票价的座位容量有剩余时，系统仍然会接受一个高票价的预订请求，即高票价的舱位等级可以利用比它低的票价等级的座位(称为每一等级的预订限制)，这样才能获得更高的收益。引入变量bki= max{n ∈Z+:ri≥Jk+1(n)- Jk+1(n +1)}，根据离散上凸函数的差分递减的性质，满足在tk时刻系统接受i 舱位等级预订请求下，并且该舱位等级预订数量≤bki时，该预订数量为最优超售水平，根据假设r0＜r1＜… ＜rm，可得到预订限制策略为bk1≤bk2≤…≤bkm。

2 算例分析

2.1 算例模拟

本节建立模拟过程，假设预订请求的到达服从参数为λa的齐次泊松过程，对于舱位等级i 的取消过程服从参数为λc马尔科夫生灭过程，因此，对于k = 1，…，K -1，有

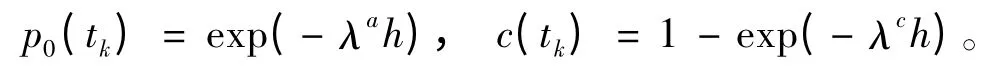
在航空售票过程中，不同时刻下不同舱位等级的预订请求密度不是一成不变的，而是随着预订时间的推移而发生改变，低票价等级的预订请求到达时间早于高票价等级的预订请求，为模拟这一条件，假设在时间点tk，不同舱位等级的预订请求到达的概率为fi(tk)，fi(tk)服从参数为αi和βi的Beta 分布，由于Beta 分布的曲线由α 和β 两个参数来决定，其形状变化幅度较大，在本文中选取适当的参数来描述不同舱位等级乘客的到达过程。不同舱位等级的预订请求到达概率计算如下:

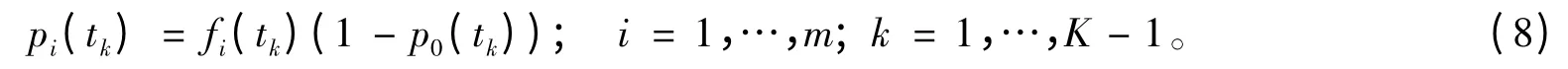
2.2 算例求解

以国内某航班数据为例，该航班的容量C 为150 个座位，设有4 个舱位等级Y、M、Q、K，票价fi分别为［1 000，800，600，400］(单位:元)，各舱位等级的需求期望和标准差如表1 所示。根据历史数据统计，取消预订的平均退款为500 元。平均取消概率为5%，为分析航班乘客到达率对于最优超售水平的影响，本文分别选取平均到达率βs=［0.91，0.93，0.95，0.97］进行分析，将预订时期分为100 个时间段，时间段间隔h=0.1，K=100，预订请求的到达参数λa=1，取消请求的到达参数λa=0.5。超售造成的拒载成本θ 为2 000 元，拒载成本大于Y 舱票价，表示由于拒载而对顾客所做出的补偿大小，另外，拒载还会导致航空公司的潜在信誉损失，但该部分损失难以定量，在文献［16］的研究中，将其假设为递增下凸函数，表示边际拒载成本递增。为便于求解，在本文中不考虑该部分损失。

表2 设定了服从Beta 分布的不同舱位等级的预订请求到达分布参数，表示不同时刻下预订请求的到达先后顺序。具体参数设置如表2 所示。

表1 舱位等级需求表

通过以上参数设置及模拟仿真过程，对模型进行求解得到的结果见表3。由表3 可以看出:Y 舱为票价最高的舱位等级，故Y 舱无预订限制，可用座位数为本航班的总超售数量，其他舱位等级都有预订限制，括号内数字表示在该超售水平下舱位等级的订座数量。当乘客平均到达率较低时，为防止飞机起飞时造成的空位虚耗损失，允许的超售数量较大;当乘客到达率增大时，总超售水平降低，以避免过多的拒载人数而造成拒载损失，同时收益也有所减少，表明乘客平均到达率越高，允许超售数量越少，同时造成拒载的人数也相对增加，导致期望收益降低。

表2 Beta 分布参数表

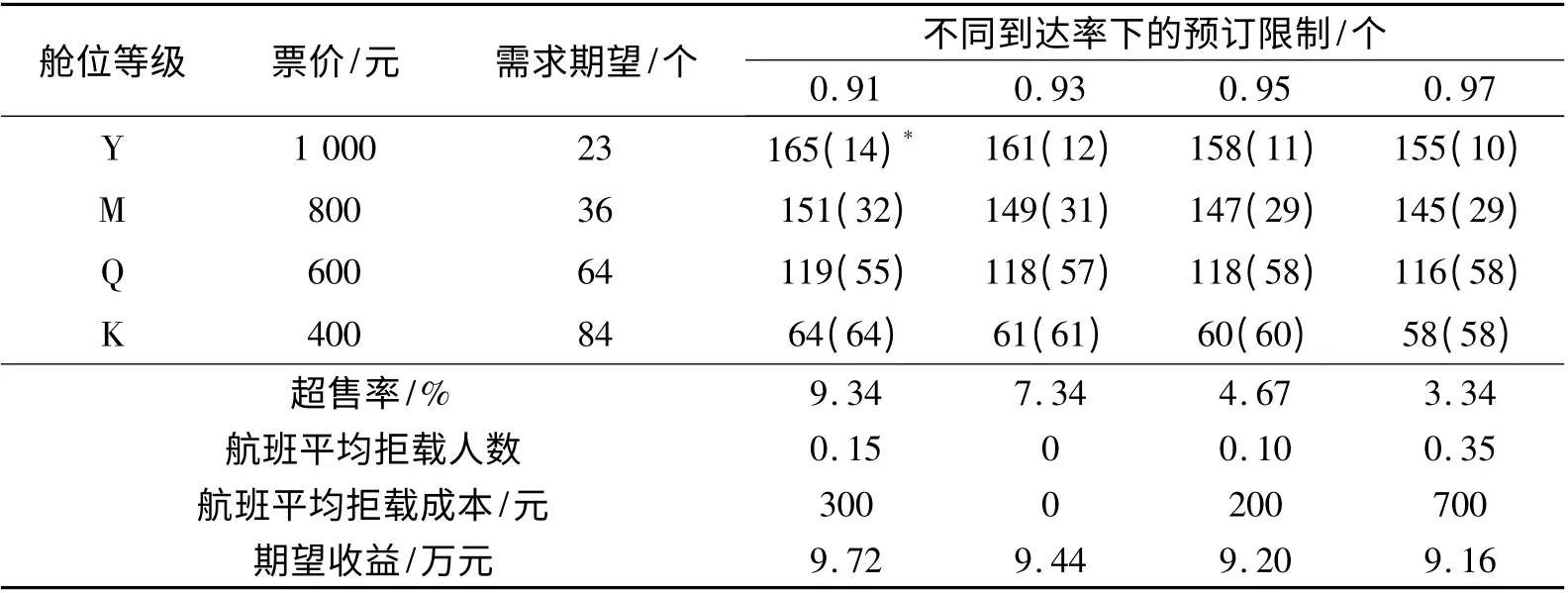
表3 舱位等级预订限制及收益情况表

另外，模型在不同的乘客到达率下，超售率均维持在较低水平，航班平均拒载人数均小于1，较好地符合实际情况。航空公司采取超售策略可以销售大于航班实际容量的座位数来增加期望收益，同时，在最优超售水平下，超售造成的平均拒载成本远远小于期望收益，因此，采取有效的超售策略可以增加航空公司的收益。

3 结束语

本文研究了考虑超售策略下航班舱位分配控制问题，以收益最大化为目标，考虑乘客平均到达率、取消率及拒载成本下建立动态舱位控制模型。根据某航班数据进行算例模拟，得到在不同乘客平均到达率下总超售数量和每一舱位等级的预订限制，其结果验证了本文模型的有效性，较好地符合实际情况，对于机票销售过程中的舱位分配优化提供一定的决策支持。但本文中假设了与舱位等级无关的平均到达率，因此考虑与舱位等级有关的退票费率，到达率下的综合建模研究有待于进一步的讨论。围绕舱位分配控制问题，下一步的研究将在以下几个方面进行:多航段下超售和舱位控制问题;动态定价与舱位控制综合问题;竞争与联盟下的舱位控制问题等。

［1］ Kevin P，Nanda P. Airline Revenue Management:an Overview of OR Techniques 1982－2001［J］. ERIM Report Series Research in Management，2002，12(2):23－52.

［2］ Rothstein M.OR and the Airline Overbooking Problem［J］.Operations Research，1985，33:237－248.

［3］ Beckman J M.Decision and Team Problems in Airline Reservations［J］. Econometrica，1958，26:134－145.

［4］ Chi Z. Airline Yield Management in a Dynamic Network Environment［D］. Cambridge:Operations Research Center，Massachusetts Institute of Technology，1995.

［5］ Chatwin R E.Continuous-time Airline Overbooking with Time Dependent Fares and Refunds［J］.Transportation Science，1999，33:182－191.

［6］ Subramanian J，Stidham S，Lautenbacher C.Airline Yield Management with Overbooking，Cancellations，and No-shows［J］.Transportation Science，1999，33:147－167.

［7］ Karaesmen I Z，van Ryzin G J.Overbooking with Substitutable Inventory Classes［J］.Operations Research，2004，52:83－104.

［8］ Lan Y，Ball M O，Karaesmen I Z. Regret in Overbooking and Fare-class Allocation for Single Leg［J］. Manufacturing ＆Service Operations Management，2011，13(2):194－208.

［9］ Belobaba P P. Air Travel Demand and Airline Seat Inventory Management［D］. Cambridge:Flight Transportation Laboratory，Massachusetts Institute of Technology，1987.

［10］ Belobaba P P.Application of a Probabilistic Decision Model to Airline Seat Inventory Control［J］.Operations Research，1989，37:183－197.

［11］ 高强.航空收益管理中舱位控制问题的研究［D］.南京:南京航空航天大学，2006.

［12］ 刘玮.航空客运收益管理中超售问题的研究［D］.南京:南京航空航天大学，2004.

［13］ 朱金福，刘玮，高强.航空客运舱位控制和超售综合静态建模研究［J］.中国管理科学，2006，14(5):68－72.

［14］ Aydin N，Birbil S I，Frenk J B G，et al.Single-leg Airline Revenue Management with Overbooking［D］.Turkey:Sabanci University，2010.

［15］ 朱金福，刘玮，姚韵.航空客运舱位控制和超售综合动态建模研究［J］.系统工程学报，2007，22(5):525－531.

［16］ Feng Y，Xiao B. A Continuous-time Seat Control Model for Single-leg Flights with No-shows and Optimal Overbooking Upper Bound［J］.European Journal of Operational Research，2006，174:1298－1316.