Easy profit maximization method for open-pit mining
2013-07-10DinisdaGama
C. Dinis da Gama
IST–TechnicalUniversityofLisbon,AvenidaRoviscoPais1,1049-001Lisboa,Portugal
Easy profit maximization method for open-pit mining
C. Dinis da Gama∗
IST–TechnicalUniversityofLisbon,AvenidaRoviscoPais1,1049-001Lisboa,Portugal
A R T I C L E I N F O
Articlehistory:
Received 18 June 2012
Received in revised form
15 December 2012
Accepted 7 June 2013
Open-pit
Profit maximization
Ore grade
Stripping ratio
Economic feasibility
A methodology applicable at any phase of a surface mining project for evaluating its current technical and economic feasibility is presented.
It requires the typically available quantitative data on the ore-body, with its three-dimensional block model developed upon accurate interpolations. Thus it allows estimations of exploitable reserves in function of various cut-off grades, such as the average grade of mineable ore, the tonnages of ore and waste rock, stripping ratios and profit estimates for different production levels.
If cost evaluations of essential mine operations are available (such as ore mining, waste removal, ore concentration, transportation, indirect project costs and expected concentrate selling prices), the methodology will provide clear indications on the economic feasibility of mining, including the best available options at any moment. Simple expressions are developed on the basis of a profit mathematical function and an application example is presented with data available from an existing iron ore deposit.
© 2013 Institute of Rock and Soil Mechanics, Chinese Academy of Sciences. Production and hosting by Elsevier B.V. All rights reserved.
1. Basic concepts
Mining is essentially governed by the knowledge obtained from three scientific disciplines: geology, mining engineering and economics.
Only through an intensive program of research and field studies can a successful mining project be implemented. This program must be carefully coordinated through a succession of pre-designed stages. Since the ultimate goal to achieve is obtaining an economic benefit upon the invested capital, that benefit is justified due to the uncertainty and risk that are involved in all those stages.
Initial studies are geological in nature, based on pre-existing information (publications, technical reports, satellite images, etc.) and usually complemented with data from exploration activities on the ground, involving studies of geology, geophysics and geochemistry. Representative sample acquisition follows from field investigation including open-pits, shallow trenches, as well as drilling campaigns. These samples are then sent to specialized laboratories for the physico-chemical characterization of minerals, allowing the creation of a database that, after appropriate computational processing, may describe the main characteristics of the deposit. Analyses of technical and economic feasibility of the project are thus required, initially with reduced available data and subsequently with the greater volumes of information in order to provide reliable evaluations of project feasibility.
Questions on the possibility of ensuring future revenues from the sale of the final product to the market, which should be higher than the investments required in all steps of the previous study, must be answered. Moreover, it is expected that these revenues will cover the necessary capital for the mining project with yields that should be higher than those of alternative financial applications.
In essence, there is always a strong interaction between the four variables represented in Fig. 1.
It is obviously necessary to involve components of engineering and economics to answer these questions.
Gama (1986) listed the following tasks required to develop this approach:
(1) Determine the geometric shape of the mineralization, by defining the spatial orientation of the ore to extract (including the distribution of its contents along the mineralized volume) as well as the barren rocky material that must be removed.
(2) Design the mining method appropriate for extracting the deposit, including the mechanical equipment to be used in operations of excavation, loading and transportation of both ore and waste.
(3) The techniques of washing/processing that will be recommended for the product concentration, in conditions of supplying the consumer market.
(4) The general costs necessary to implement the project, from investments in exploration and recognition of the deposit, to feasibility studies and engineering design of the mine, not to mention the corresponding indirect costs of production (offices, business administration, social services, etc.)
(5) The funds to be spent as payments of taxes, miscellaneous fees and compliance with environmental protection rules will apply.
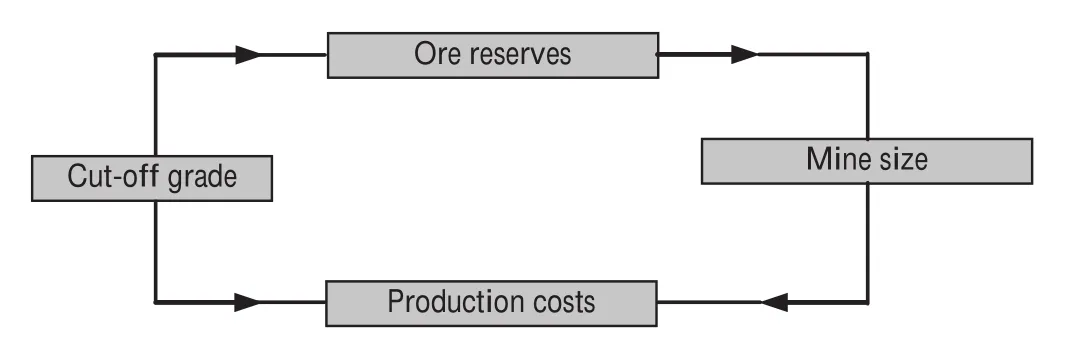
Fig. 1. The four main variables influencing the economic feasibility of a mining project, according to Gentry and O’Neil (1984).
There are several criteria to quantify all the variables listed above, being more used that proposed by Plewman (1970), Barnes (1980), and Hustrulid and Kuchta (2006).
It consists in defining the hourly profit functionL($/h) by the following relation:

whereP(t/h) is the hourly production of the mine, which is sent to the mill;T(%) is the average grade of ore that is mined;U(%) is the metal recovery rate obtained in the concentration plant;V($/t) is the sales price per ton of metal (or useful substance) out of the plant;M($/t) is the cost of mining per ton of excavated ore;E($/t) is the cost of removal per ton of waste material;R(t/t) is the instantaneous waste/ore stripping ratio;B($/t) is the cost of processing per ton of ore that enters the plant; andF($/h) is the hourly incidence of fixed costs, capital, taxes and other indirect charges.
Fig. 2 schematically represents those variables.
The profit function can also be formulated in unit values (per ton or cubic meter of ore), by assigning a unit profit function L′($/h), which is given by

In all these variables, there are two geological characteristics, which have great importance: the stripping ratioRand the grade of oreT. It is therefore essential to determine what their extreme values are which may lead to a zero profit.

Fig. 2. Flowchart of production in an open-pit mine, with its main attributes.
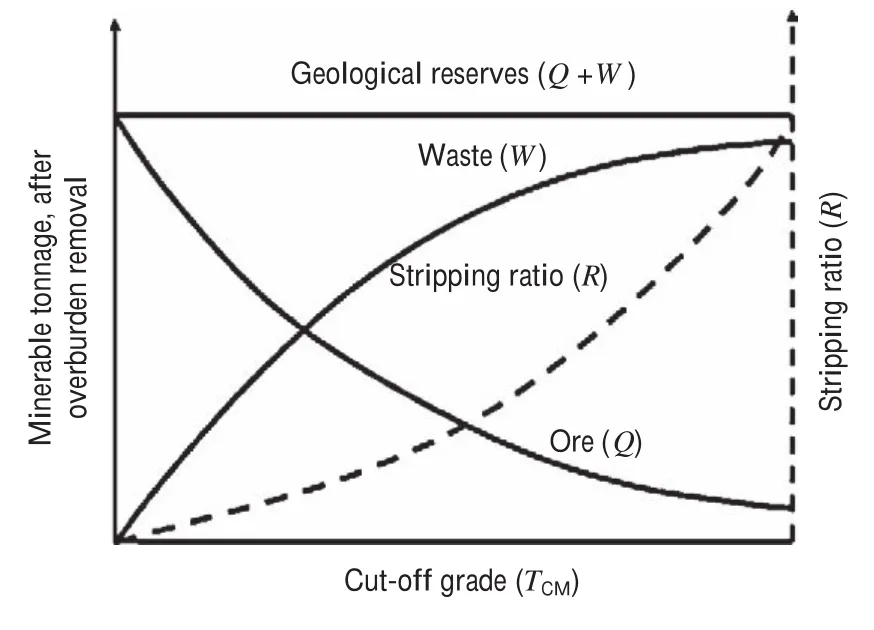
Fig. 3. Typical variations of exploitable reserves (Q + W) and stripping ratio (R) as a function of the cut-off grade (TCM).
Thus, theminimumallowablecut-offgradeis provided by the expression:

meaning the grade content that separates the exploitable material (ore) from the one which is sent to the heap (waste).
In the same way,themaximumallowablestrippingratiois given by

representing the largest amount of overburden material that can be removed in order to extract one ton of ore with an average gradeT, above the level ofTCM.
In practice, the operating conditions of any mine should be set away from those where profit can either be zero or negative, so thatTCMandRmaxare limit values not to be exceeded, considering that the other variables are unchanged.
It is worth noting the instant relationships that must exist between the quantities of ore, waste rock and the actual cut-off grade. Fig. 3 shows this typical variation, by means of introducing the concept of geological reserveQ+W, which is defined as the sum of the quantities of ore and waste, as well as showing a typical variation of the stripping ratio with cut-off grade.
Another relevant concept is theallowablestrippingratioRad, which is defined upon the consideration of a minimum profit (Lmin) that must always exist, and it is given by

Therefore, the economic control of mining should be conducted in a continuous way and it must be based on the assessment of the levels of the ore gradeTand stripping ratioR, which should satisfy the following conditions:

2. Correlations between ore body model and profit function
The ability to formulate three-dimensional block models for any mineral deposit can be used to evaluate the conditions of its exploitability.
For this purpose, it is important to correlate mathematically the relevant variables in the profit function and its dependence on the cut-off gradeTC. In particular, there are three variables that can betreated alike: the ore reserveQ, the average content of the ore gradeT, and the stripping ratioR, by means of three functions such as:


Table 1 Summary of reserves calculated for the Mua ore body, for various levels of cut-off grade.
Substituting these variables in the profit function formula, a direct relationship between profit and cut-off grade is obtained in order to allow a continuous monitoring of the mining operation economics.
One can thus determine relevant characteristics of the project, such as the optimal cut-off grade (defined as one that maximizes profit), the adequate stripping ratio and the maximum overall profit.
The above can be illustrated with simple mathematical functions, of the following type:

wherea0,a1,b0,b1,c0, andc1are constant coefficients.
It is then possible to establish equations linking operational profit with the cut-off grade and then find the cut-off grade value that leads to that maximum profit.
In this way, thetotalprofitwould be given by the expression:
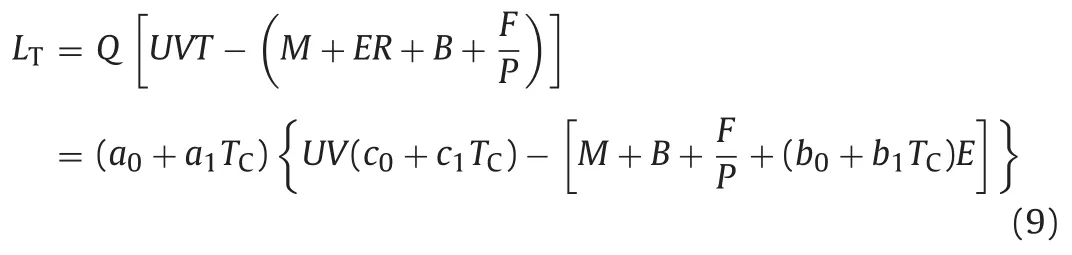
To determine the maximum of this function, it can be derived with respect toTC, and afterwards making it equal to zero in order to determine theoptimalvalueofcut-offgradeTOP, which is given by

This important expression is of great interest, for it involves the four main variables included in Fig. 1 and may determine any instantaneous balance between them, as well as providing advantageous solutions for mine production planning.

Table 2 Application example: numerical values of variables involved in the profit function.
3. Application of real geological data
Table 1 contains the main results of the geological characterization of the iron ore deposit of Cabec¸ o de Mua (Portugal), before applying economic considerations.
In addition, a set of economic parameters were determined upon feasibility studies on the project, which are shown in Table 2.
From these values it follows that the unit profit function is given by the relation:
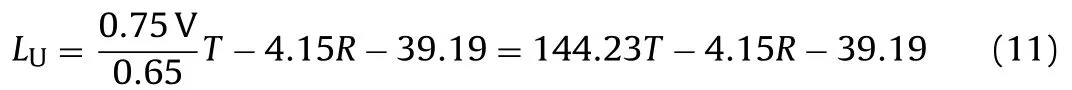
resulting in (for the case ofR= 0) a minimum cut-off grade of 27.17% Fe.
As indicated in Table 1, the average grade of the entire deposit is 39.55% Fe, a value that is well above the minimum cut-off grade, thus indicating favorable conditions of exploitability.
Other parameters of interest can be calculated in order to seek more profitable opportunities.
In effect, on the basis of data presented in Table 1, it is possible to quantify the three functions mentioned above (Q,RandT), as Table 3 shows.
It must be emphasized thatRmay not assume negative values, so in a situation whereTC< −b0/b1, the values ofb0=b1= 0 must be used.
Substituting the numerical data of Table 3 in the expression for calculating the optimal cut-off grade, we obtainTOP= 25.17% Fe, leading to a maximum total profit of:


Table 3 Data set of Q, R and T as function of cut-off grade, subjected to statistical regression analysis (as all correlation coefficients are greater than 0.88, there is no need to use polynomials with a degree higher than 1).
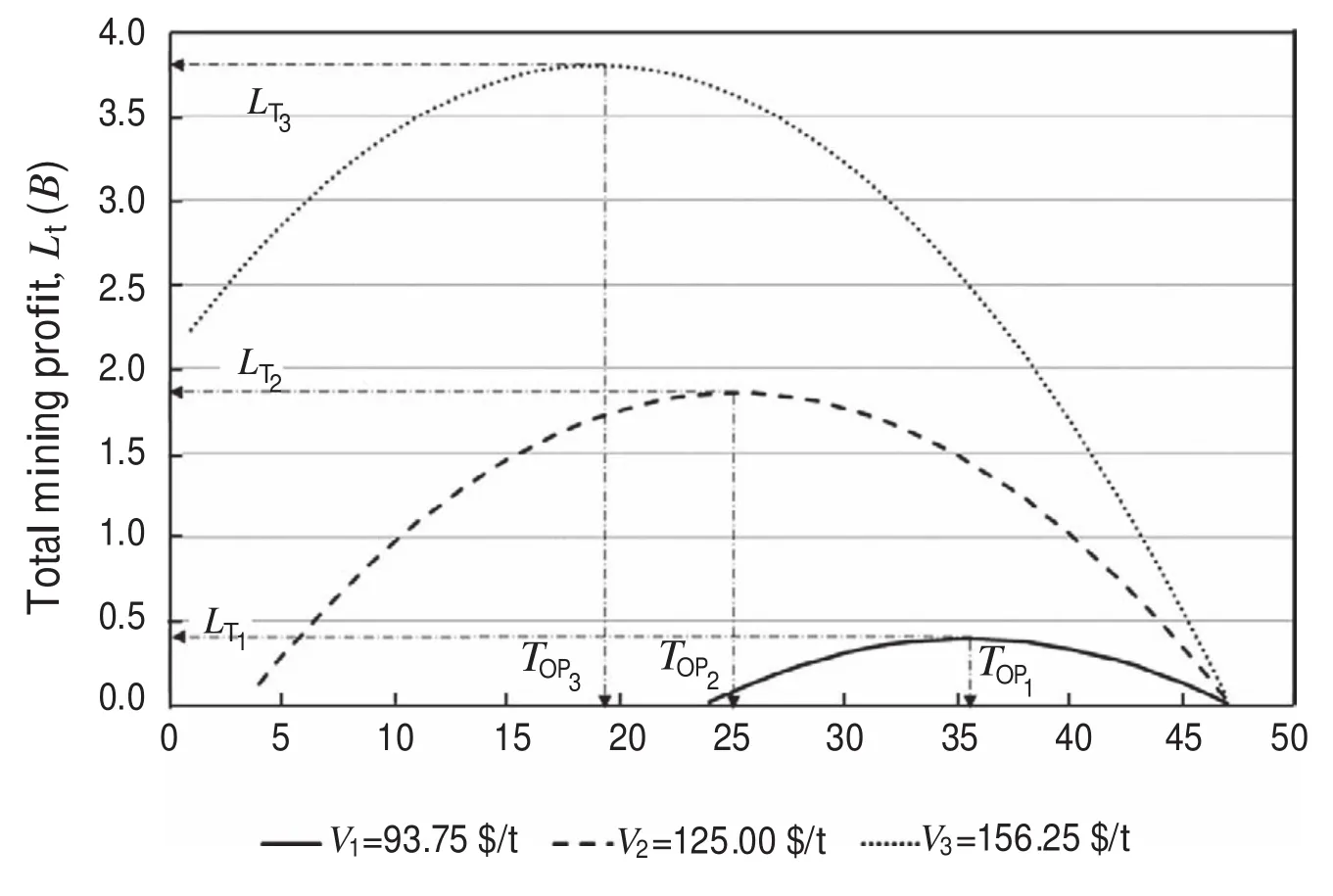
Fig. 4. Sensitivity analysis of effects of selling price variations.
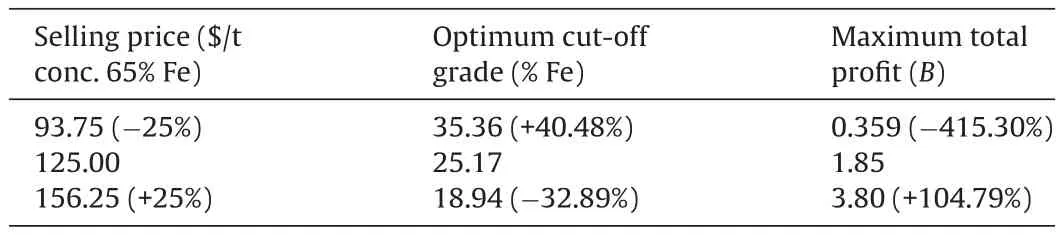
Table 4 Values of the optimal cut-off grade and the maximum total profit for a range of iron ore concentrate selling prices of ±25% the basic value of 125.00 $/t.
The method opens the possibility of performing sensitivity analyses on different project variables, for example, by varying the iron ore concentrate selling price, which is the most important exogenous variable.
Assuming values of ±25% on the price shown in Table 2, a set of results may be gathered, as listed in Table 4, which provides a range of solutions that can contribute to adequate decision-making on project management. Such results are depicted in Fig. 4.
It may be observed that the changes in terms of optimal cut-off grade and the maximum total pro fit fluctuations are not proportional to the selling price variations, showing in particular a great variability for the maximum total pro fit.
The situation is particularly dif ficult for the lowest selling price, which requires a much greater optimum cut-off grade, thus decreasing the volume of exploitable reserves and leading to higher production costs due to the need for larger quantities of waste removal.
4. Conclusions
It was sought to describe the usefulness of an expedite approach to permanently control surface mining projects, with the aim of determining the optimum values of the main variables that in fluence project pro fitability.
Given a multitude of situations that might be encountered during the life of any mine operation, its managers must possess essential tools for rapid decision-making criteria and adjustment to reality. Such methods do not invalidate the applicability of more complex methodologies, such as integrated computational models, although these will lead to many dif ficulties in providing precise input data that sometimes are not available in mining companies.
Barnes MP. Computer-assisted mineral appraisal and feasibility. New York: Society for Mining Metallurgy; 1980.
Gama CD. Methodology for the control of mining pro fits. IPT Publication No. 1661. Brazil: Institute of Technological Research of São Paulo; 1986.
Gentry DW, O’Neil TJ. Mine investment analysis. New York: Society of Mining Engineers; 1984.
Hustrulid W, Kuchta M. Open pit mine planning & design. 2nd ed. London: Taylor & Francis; 2006.
Plewman RP. The basic economics of open pit mining. In: Symposium on planning open pit mines; 1970.

C. Dinis da Gamais a Mining Engineer (IST, 1963), and has Master of Science (University of Minnesota, USA, 1970), PhD (1971), Aggregated (1973), Full Professor (1974), Free Professor, USP, Brazil (1983), Full Professor IST (1994). He is the Head of Geotechnical Center since 2000. His main teaching and research topics are surface and underground mining, rock mechanics and environmental geotechnics. He has consulting activities in Portugal, Angola, Brazil, Spain, Italy, Poland, Peru and China. He is a member of two Expert Committees of the European Union in Brussels, during 12 years. He has done supervision of 15 PhD programs and more than 30 MSc. He has more than 320 technical publications.
∗Tel.: +351 961901868.
E-mail address: dgama@ist.utl.pt
Peer review under responsibility of Institute of Rock and Soil Mechanics, Chinese Academy of Sciences.
1674-7755 © 2013 Institute of Rock and Soil Mechanics, Chinese Academy of Sciences. Production and hosting by Elsevier B.V. All rights reserved.
http://dx.doi.org/10.1016/j.jrmge.2013.07.001
杂志排行
Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Easy profit maximization method for open-pit mining
- A discontinuum-based model to simulate compressive and tensile failure in sedimentary rock
- Landslide disaster prevention and mitigation through works in Hong Kong
- Reply to Discussion on “A generalized three-dimensional failure criterion for rock masses”
- Discussion on “A generalized three-dimensional failure criterion for rock masses”
- Effects of physical properties on electrical conductivity of compacted lateritic soil
