基于多级模糊综合评定法的交流接触器最佳合闸相角的确定

杨怡君，苏秀苹，黄绍伟，李俊峰，4

（1.河北工业大学电磁场与电器可靠性省部共建重点实验室，天津300130；2.河北工程大学信息与电气工程学院，河北邯郸056038；3.山东大学控制科学与工程学院，济南250100；4.邯郸学院物理与电气工程系，河北邯郸056001）

基于多级模糊综合评定法的交流接触器最佳合闸相角的确定

杨怡君1，2，苏秀苹1，黄绍伟3，李俊峰1，4

（1.河北工业大学电磁场与电器可靠性省部共建重点实验室，天津300130；2.河北工程大学信息与电气工程学院，河北邯郸056038；3.山东大学控制科学与工程学院，济南250100；4.邯郸学院物理与电气工程系，河北邯郸056001）

采用二级模糊综合评判技术确定交流接触器的最佳合闸相角.首先利用正交试验建立了CJ20-25型交流接触器21个动态特征参数的原始数据库，然后按照二级模糊综合评判方法计算得到唯一评判指标.考虑到产品性能的差异，利用每台样品的评判值拟合曲线求解均值fφ和方差Sφ，再进行一级模糊综合评价，综合考虑确定了最佳合闸相角的范围，且实验结果和仿真结果基本一致.实验结论可为同类电器产品性能的评判提供较为精确的试验条件.

交流接触器；合闸相角；二级模糊综合评定；动态响应

接触器主要用于频繁接通或分断交、直流主电路和大容量的控制电路，是电力拖动和自动化控制系统中不可缺少的量大面广的低压电器产品.对于一定结构尺寸参数的交流接触器，其动态过程极其复杂，且动态特性取决于电源电压接通时刻的合闸相角[1-2].大量实验证明，合理的设计可有效减少触头的二次振动[3-5].在最佳合闸相角合闸，可最大限度地降低动静铁心的碰撞能量，防止触头二次弹跳，降低触头接通磨损，提高电寿命、机械寿命和接通能力.文献[6-7]以动铁心闭合速度Vr，弹跳时间Tr，三相动触头的闭合速度VA、VB、VC以及触头的弹跳时间TtA、TtB、TtC进行二级模糊综合评定，考虑的因素不多，但研究手段可行.在文献[6-7]提供的评价指标基础上，本课题组以CJ20-25型交流接触器为测试对象，结合文献[8-12]的研究成果，利用光机电接触器动态测试装置，检测合闸过程中影响触头和铁心弹跳的21个动态特征参数.采用二级模糊综合评判理论将其综合为一个评定指标，以此计算出最佳合闸相角范围.

1 动态特性参数的获取

动态特性参数选取是否合适，直接影响最佳合闸相角判定结果的精确性和合理性.这里应该选取最能体现接触器吸合过程的动态特性参数.当线圈通电后，在电磁力的作用下，动铁心以较高的速度带动触头运动，先与静触头发生碰撞，引起触头的多次弹跳，然后与静铁心发生碰撞，再次产生弹跳.每一次弹跳都会对触头材料产生侵蚀，影响接触器的电寿命.经过检索大量文献得知，接触器的机械寿命和电特性与触头弹跳情况以及铁心碰撞时的速度、冲量存在直接的关系.为消弱上述两大方面因素的影响，文献[1，4-12]选择了触头一次弹跳时间、一次弹跳次数、动静触头相碰前的末速度、动静铁心相碰前的末速度进行了动态测试.可以看出，对接触器工作过程的动态测量，均采用了与触头弹跳和铁心碰撞相关的物理量.因此，本文利用光机电接触器动态测试装置，对CJ20-25型交流接触器在0°～180°之间等间隔5°选取合闸相角，测量样品在这些合闸相角吸合时的21个动态响应特性参数，如图1所示，每个参数均测量5次.

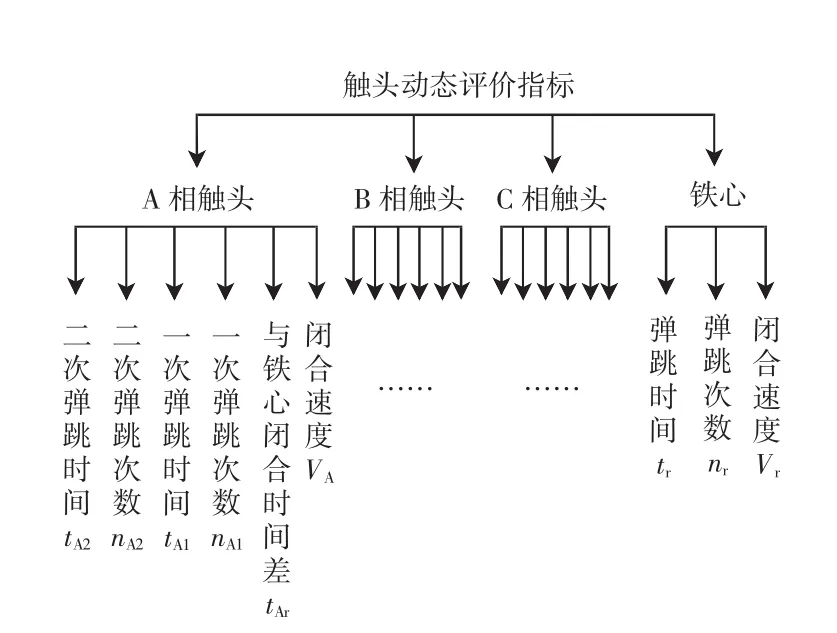
图1 模糊评判层次结构图Fig.1 Hierarchy of fuzzy evaluation

由于实测数据很多，这里仅列出第1次测量的部分实验原始数据，如表1所示.

表1 1#样品动态特性测试的部分原始数据Tab.1Part test original data of 1#sample dynamic characteristics

2 模糊综合评判

模糊综合评判法是在模糊环境中进行多因素信息的处理，对某些事物关于某种目的做出综合判断，可以处理其他方法无法处理的模糊信息，因此能够将由多个动态特征参数表征的交流接触器触头动态响应的模糊性用数学模型进行表达、评价.实施步骤如图2所示[1，6-9]：

图2 模糊评判实现步骤Fig.2 Steps of fuzzy evaluation

2.1 一级模糊综合评判

本课题考虑因素很多，若用一级模糊综合评判模型，一是权数难以较为合理地分配，二是因权重系数都很小，会出现“泯没”大量单因素评判信息的情况.所以考虑采用二级模糊综合评判，即将考查的21个动态响应过程相关的参数划分为2层，如图1所示.

2.1.1 评判指标因素集U

按照图1采用二级因素集，令U={U1，U2，U3，U4}，其中U表示二级模糊综合评判结果，即衡量样品动态响应好坏的唯一评价值；U1～U3为一级模糊评判结果，分别表示A相～C相触头一级模糊评判的评判值；U4表示铁心一级模糊评判的评判值.其中U1={tA2，nA2，tA1，nA1，tAr，VA}，U2={tB2，nB2，tB1，nB1，tBr，VB}，U3={tC2，nC2，tC1，nC1，tCr，VC}，U4={tr，nr，Vr}.U1～U3各因素含义类似，如图1所示.

2.1.2 评判集合V

评判集合采用5级评语集，即Vi={很好，好，一般，较差，很差}（i=1～4）.

2.1.3 单因素评判矩阵R

对于每个合闸相角下10组数据，取其对应参数的最大值和最小值.选取图3所示三角形隶属函数，计算得到各指标对应的分级标准值如表2所示.

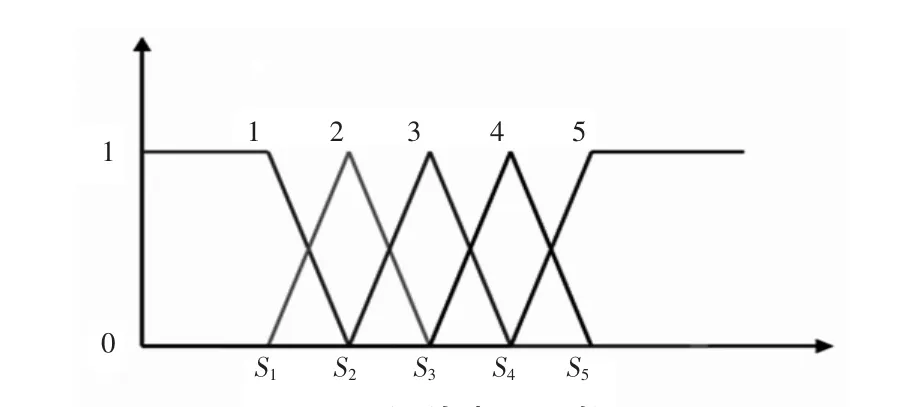
图3 评价隶属函数图Fig.3 Membership function

表2 评判指标分级标准值Tab.2Index classification value for fuzzy evaluation

各评判级别是从最小值至最大值之间的等分点，用S1～S5表示.计算每个评判指标对每个评判等级的隶属度，构成模糊评判矩阵R1～R4.铁心吸合情况与触头情况不同，这里仅以A相触头和铁心吸合2种情况表示.

2.1.4 模糊综合评判权重矩阵

（1）一级模糊综合评判权重矩阵Ai.在一级模糊综合评判中，考虑到触头的二次弹跳比一次弹跳的影响大，给其分配较大的权重.对于铁心吸合情况，考虑到其闭合速度比弹跳的影响小，权重较小.因此，Ai=（0.4，0.2，0.2，0.1，0.05，0.05）（i=1～3），A4=（0.4，0.4，0.2）.

（2）二级模糊综合评判权重矩阵A.考虑到铁心吸合小于三相触头的影响，故设A=（0.3，0.3，0.3，0.1）.此时一级模糊综合评判矩阵Bi(1×5)=Ai·Ri（i=1～4）

2.1.5 确定二级综合评判矩阵R′

由上述一级模糊评判评价集B1～B4得二级综合评判矩阵R′(4×5)为：R′=（B1，B2，B3，B4）T

模糊综合评判集为：B′=A·R′=（b1，b2，b3，b4，b5）

2.1.6 计算模糊综合评判值F

采用加权平均法对评判指标进行评分处理.前述模糊综合评判中评判指标已经归一化，将很好、好、一般、较差、差等级分别用5、4、3、2、1量化表示，则可以计算得到评分结果评判值越大，表征触头动态响应越好；评判值越小，表征触头动态响应越差，以此为依据可确定最佳合闸相角.

2.2 二级模糊综合评判结果

由于每台样品在每个合闸相角下的每次测试都需计算动态响应模糊综合评判值F，涉及的数据十分庞大.在0°～180°之间等间隔5°选取合闸相角，每个相角下测量5次，共计185组数据.1#～9#样品第一次测量结果的模糊综合评判值如表3所示.

表3 模糊综合评判结果表Tab.3Fuzzy evaluation values of 1#～9#

由表3可以看出，同一样品在不同合闸相角下的评判值不同，不同样品在同一合闸相角下的评判值不同.由于对每个合闸相角下的每次测量结果均进行了动态响应指标的计算，因此得到了9台样品的触头动态响应指标F与合闸相角φ的关系.其中2#与7#试品的二级模糊综合评判值F与合闸相角φ的F-φ关系及拟合曲线如图4所示.

图42 #与7#样品的动态响应评价指标图Fig.4 Curves of 2#and 7#samples evaluation index

对图4（a）中离散点进行曲线拟合，并同时得到置信度为95%时的上下限，其拟合线方程为：

用同样的方法也可以获得其他样品的拟合曲线及拟合方程.对拟合方程求一阶导数，即可求得评价值取得最大值时的合闸相角.计算可知，2#样品的合闸相角在20°～35°时，模糊综合评判值F较大.通过比较图4可以发现，2台样品的评价值变化趋势相似，但曲线波动幅度存在很大差异，且各台样品的最大评价值对应的合闸相角并不相同.

3 最佳合闸相角的确定

由于不同产品动态响应的分散性，同一台接触器即使在同一合闸相角合闸时的性能也不完全相同.本文确定最佳合闸相角的思路是：对9台样品动态响应拟合曲线的下限进行分析，分别得到合闸相角为0°，1°，...，180°时各个样品动态响应指标的均值和方差，并由均值矩阵Fφ=[fφ1，fφ2，…，fφ180]1×180和方差矩阵Sφ= [sφ1，sφ2，…，sφ180]1×180再进行一级模糊综合评价，依据评价值的大小确定最佳合闸相角.一级模糊评价方法如前所述，只是评价因素集和权重矩阵有所不同.下面简单介绍计算步骤.

3.1 评判指标因素集U

式中：sφj为n个接触器在合闸相角j下的动态响应标准偏差.

3.2 五级评语集V和权重矩阵A

V={v1，v2，v3，v4，v5}={很好，好，一般，较差，差}，根据实际情况，将偏差的权重设置稍大一点，权重集可设定为：A=（a1，a2）=（0.4，0.6）

3.3 模糊关系矩阵R和综合评判集B

仍然选择三角形隶属函数，按照同样方法得到每个合闸相角下的模糊关系矩阵R′=[R1，R2，…，R180]：

选用模型M（·，+）得到Bj=A·Rj，进而得到模糊综合评判集B={B1，B2，…，B180}.

3.4 绘制综合评判值F曲线

采用加权求和平均法对评判指标进行评判值的计算，则可以计算得到评价值Fj（j=1，2，…，180），如图5所示.

图5 最佳合闸相角的模糊综合评分结果Fig.5 Results of best switching phase angle in fuzzy comprehensive evaluation

由图5可以看出，评价值最大的取值区间对应的接触器最佳合闸相角为23°～32°.在此范围内，触头动态响应指标评判值均大于4.46，相角范围为10°，也可满足测试装置选相合闸的精度要求.

3.5 计算值与仿真值对比

采用建模软件Pro/E建立交流接触器操动机构的三维模型，通过Pro/E和ADAMS的专用接口程序Mech/Pro将Pro/E所建的模型导入到ADAMS软件.这里仅以样品2和样品7为例，将样品的结构参数作为模型的输入值，进行实验结果和仿真结果的比较，如图6所示.

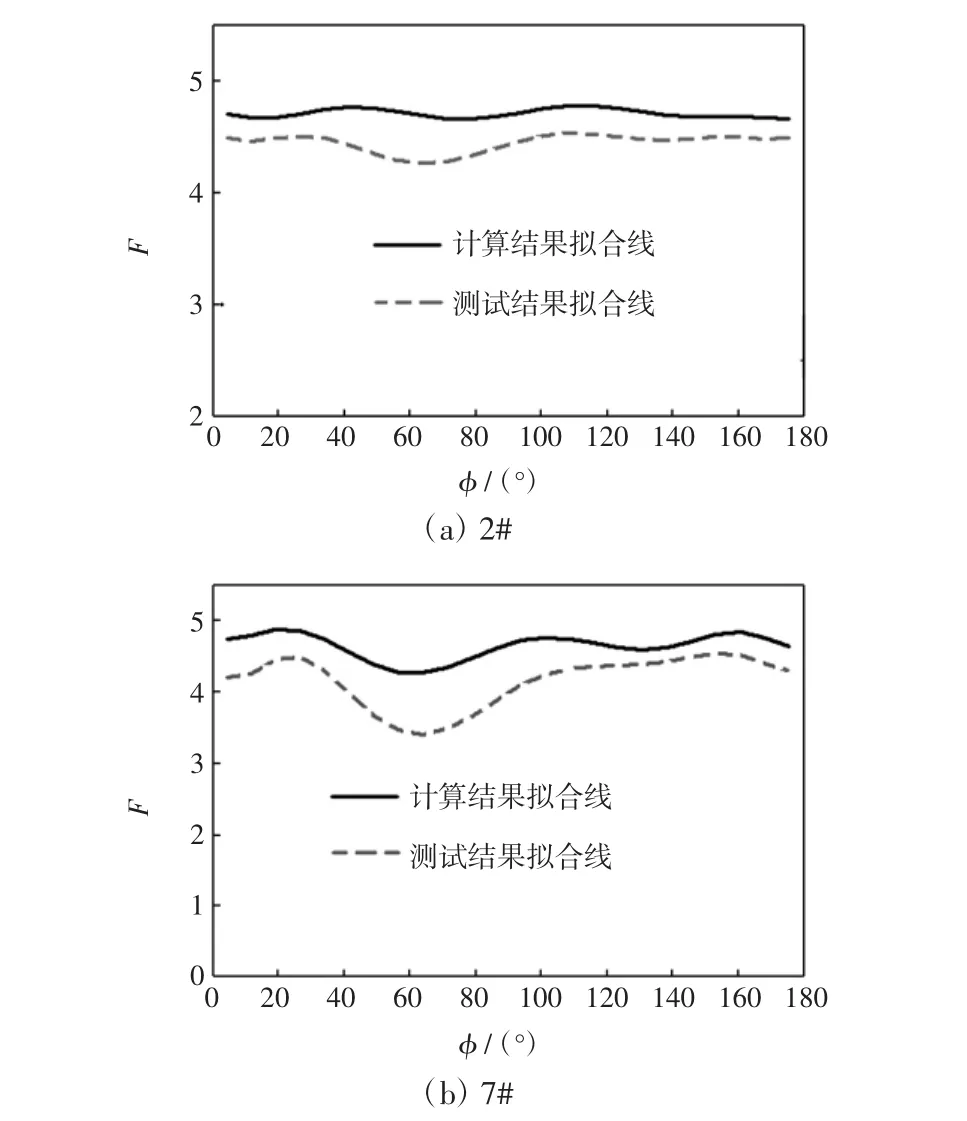
图62 #和7#样品仿真结果与实验结果的比较图Fig.6 Comparison between simulation results and actual measuring results of 2#and 7#samples

由图6可见，实验结果和仿真结果两者的拟合线变化趋势是相同的，虽然仿真结果所得评价指标相对要高一些，但总体来说，仿真结果和试验结果比较吻合，在最佳合闸相角23°～32°处评判值较其他高些.

4 结束语

针对交流接触器触头动态响应过程的诸多影响因素，获取21个动态响应参数的原始数据，采用二级模糊综合评价理论量化动态性能指标F.为了全面评价每台样品的触头动态响应特性，提出2个指标fφ和sφ，分别表示每个合闸相角下综合评判值的均值和方差.结合模糊评价理论，确定CJ20-25型交流接触器的最佳合闸相角为23°～32°，控制精度更高，满足实际控制要求.后续研究中，可以依据最佳合闸相角进行动态测试，计算各台样品的不确定性指标，对单台样品以及整批产品进行不确定性的评价和区间估计，为用户提供直观的量化指标.

[1]陈德为，张培铭．转动式交流接触器合闸相角的模糊优化设计与控制[J]．南昌大学学报：工科版，2009，31（2）：151-155．

[2]李兴文，陈德桂，孙志强．交流接触器动态过程及触头弹跳的数值分析与实验研究[J]．中国电机工程学报，2004，24（9）：229-233.

[3]崔芮华，贾峰，柳杰，等．交流接触器电磁机构动态仿真分析[J]．微计算机信息，2006，22（71）：286-288．

[4]李兴文，陈德桂，孙志强，等．交流接触器动态过程及触头弹跳的数值分析与实验研究[J]．中国电机工程学报，2004，24（9）：229-233．

[5]纽春萍，陈德桂，李兴文，等．交流接触器触头弹跳的仿真及影响因素[J]．电工技术学报，2007，22（10）：87-90．

[6]SU Xiu-ping，SUN He-xu，LI Jie，et al．Evaluation of AC contactor′s dynamic characteristics using fuzzy techniques[C]// PowerSystems Conference and Exposition.Seattle：IEEE，2009.

[7]SU Xiu-ping，LU Jian-guo，GAO Bing-jun，et al．Determination of the best closing phase angle for AC contactor based on game theory[C]//Proceedings of the Annual Holm Conference on Electrical Contacts，2007＆Proceedings of the 52nd IEEEHolmConferenceonElectricalContacts.Montreal：IEEE，2006：188-192．

[8]陈弘，陈德为．基于熵权AHP法的转动式交流接触器合闸相角优化[J]．电气制造，2009（12）：52-57.

[9]林苏斌，缪希仁，张培铭．基于DSP与可视化技术的接触器的动态测试装置研究[J]．福州大学学报：自然科学版，2004，32（1）：38-42.

[10]缪希仁，林苏斌，张培铭．基于动态测试技术的交流接触器性能评判系统[J]．电工电能新技术，2006，25（3）：9-12，63.

[11]林苏斌，缪希仁，张丽萍．接触器动态参数测试及性能评估装置[J]．电气应用，2007，26（3）：86-90.

[12]吴玮，伍小杰，夏晶晶，等．交流接触器吸合过程的数据采集系统实现[J]．微计算机信息，2001，31：79-81.

Determination of best closing phase angle for AC contactor based on fuzzy comprehensive theory

YANG Yi-jun1，2，SU Xiu-ping1，HUANG Shao-wei3，LI Jun-feng1，4
（1.Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability，Hebei University of Technology，Tianjin 300130，China；2.School of Information&Electrical Engineering，Hebei University of Engineeering，Handan 056038，China；3.Shool of Control Science and Engineering，Shandong University，Jinan 250100，China；4.Department of Physics&Electrical Enginering，Handan College，Handan 056001，China）

The best closing phase angle of AC contactor is ascertained based on multi-level fuzzy comprehensive theory.A database containing 21 dynamic parameters for CJ20-25 AC contactor is established by means of orthogonal experiment，and then the only evaluation index is determined by two-stage fuzzy comprehensive evaluation. Considering the differences between samples′performance，the average value fφand mean square error Sφin the fitting curve of each product′s evaluation value are solved，and then the best angle is determined by using the one-level comprehensive evaluation.The relsult of experiment is consistent with simulation，so it will provide more accurate equipment condition to evaluate the similar devices′performance.

AC contactor；closing phase angle；two-stage fuzzy comprehensive evaluation；dynamic response

TM572.2

A

1671－024X（2013）06－0063－05

2013-05-20

国家自然科学基金资助项目（50577015）；浙江省低压电器产业技术创新战略联盟项目（2010LM104-07）

杨怡君（1979—），女，博士研究生，讲师.

苏秀苹（1966—），女，博士，教授，博士生导师.E-mail：suxiuping@hebut.edu.cn