基于综合目标函数的神经网络多新息辨识算法

徐宝昌,刘新乐

(中国石油大学地球物理与信息工程学院,北京 102249)

基于综合目标函数的神经网络多新息辨识算法

徐宝昌,刘新乐

(中国石油大学地球物理与信息工程学院,北京 102249)

为提高动态神经网络学习算法的辨识精度及抗噪性能,提出一种基于综合目标函数的多新息辨识算法。该算法基于多新息理论在最小均方误差目标函数中引入一辅助项构造综合目标函数,利用该目标函数进行网络输出层权值的训练,并采用牛顿法推导出输出层权值的递推计算公式。与已有二阶学习算法相比,新算法鲁棒性强,收敛速度快,辨识精度高。仿真结果验证了算法的有效性。

系统辨识；综合目标函数；神经网络；多新息

人工神经网络以其强大的非线性变换能力被广泛应用于非线性系统模型[1-4]。很多学者将不同的优化方法用于网络结构的选择与权值的训练,形成了各具特色的学习算法[5-8]。然而,学习算法的性能跟目标函数同样有很大关系。不同于构造常规最小均方误差目标函数,文献[9]针对前馈型网络构造新的目标函数,提出了一种新的优化算法,但是该方法中对样本的剔除没有依据；文献[10]通过在目标函数中引入辅助项,以增强算法的抗噪性能,但仅用于稳态网络输出层的权值训练；文献[11]提出了基于泛化损失率的目标函数,并将粒子群算法用于神经网络权值训练,改善了网络的收敛性能与泛化能力,该算法过于复杂。而且,在权值训练过程中,已有的方法都是利用的单新息参数修正技术。近年来,丁锋等[12-13]相继提出了多新息理论并用于参数辨识,可有效保证辨识性能。笔者研究动态非线性系统的神经网络辨识问题,针对训练样本受噪声污染严重的实际情况,提出一种新型的综合目标函数,基于该目标函数和多新息辨识理论对网络输出层的权值进行训练。

1 非线性系统辨识的神经网络模型

离散的非线性时变系统可以描述为

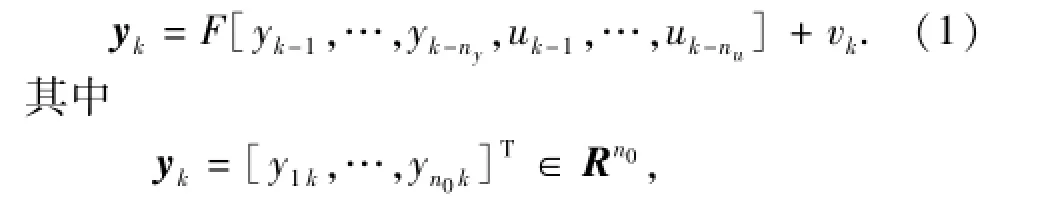
式中,yk和uk为系统输出、输入向量；vk为零均值白噪声序列；F为未知的非线性函数。

设综合输入

由于F未知,用具有rn个隐含层的前向神经网络逼近,即利用输入、输出样本集ξ={(Uk,yk)|k=1,…,m}对此神经网络进行学习训练,使其在某一准则下逼近于非线性系统(1)。对∀k,神经网络输出层和各隐层输出向量分别为

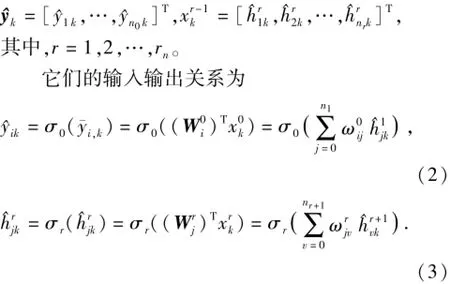
2 算法分析

2.1 算法推导

对于神经网络系统而言,实际采集的训练样本总会受到噪声的污染,即使经过一定的处理,噪声的影响依然存在。在对网络权值训练时,如果依然采取常规最小均方误差的目标函数,受噪声污染的样本会使得网络在训练的过程中出现坏数据,甚至导致矩阵奇异,严重影响算法的收敛性,降低了算法克服噪声影响的能力。而且,单新息参数修正没有完全利用过去的误差信息,难以保证参数辨识的性能[13],即k时刻的参数估计θ(k)是在θ(k-1)的基础上,由增益向量h(k)与单新息e(k)乘积来修正: θ(k)=θ(k-1)+h(k)e(k)。多新息辨识理论就是将增益向量与新息向量拓展为矩阵,在每次迭代中,利用k=k-P+1到k=k时的P组数据对前一时刻的参数进行修正。本文即采用多新息理论,同时利用输入输出数据的先验信息,在LMSE目标函数中引入一辅助项,构成新的综合目标函数。基于该目标函数进行输出层权值训练,能够提高算法的学习速度和精度,增强算法的抗噪能力。

综合目标函数的形式为

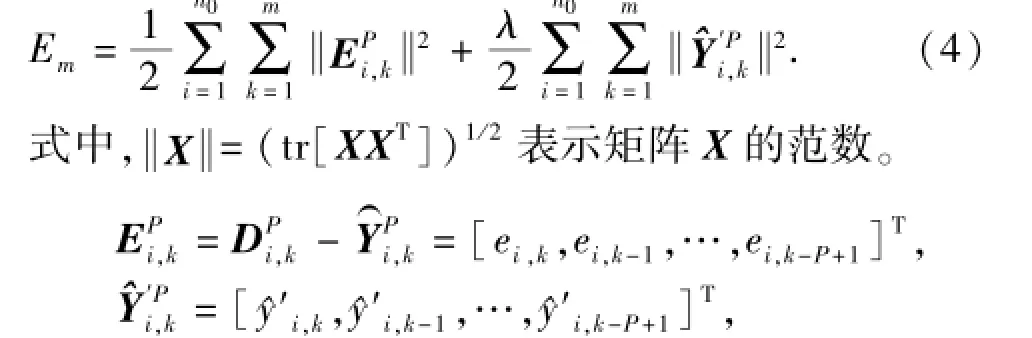
式(4)中第一项将基于单新息的LMSE目标函数进行了拓展,P值的选取决定了新息向量的维数,利用遍历数据信息,有效提高学习算法的收敛速度。第二项用于约束网络输出的平滑性,利用P维网络输出对输出层权值的一阶导数进行在线调整实现。

定理1对于多层前向神经网络模型,基于式(4)综合目标函数,输出层权值的递推计算公式为

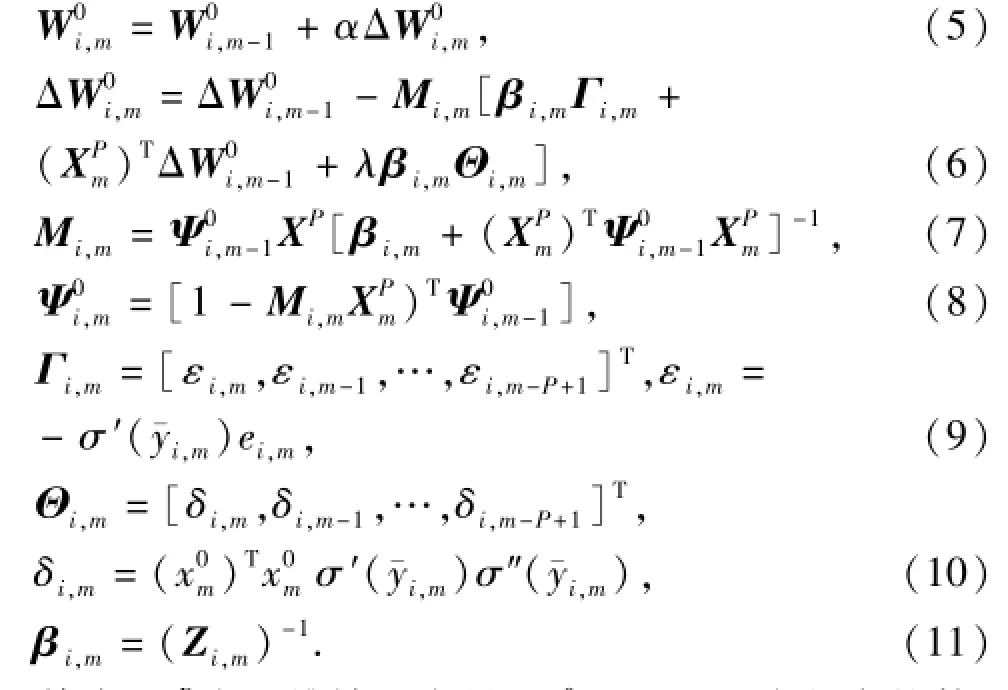
证明 式(4)可化为如下形式:

利用Gauss-Newton法求解式(12)的最小化问题,可得输出层权值的递推计算公式为

故式(13),(16),(18),(22)组成了输出层权值的递推计算公式,每次输入一个新的样本,利用P维新息对权值进行修正,所有样本输入,即完成一次训练。增加训练次数,直至满足精度的要求。在训练过程中,要始终保证Hessian矩阵的非奇异性,从而保证计算的稳定性,所以的初始化矩阵=ωI,ω应取一很大的数。定理1得证。0

对于输入层和隐含层权值的训练,本文采用文献[14]中提出的Karayiannis方法,该方法基于常规LMSE目标函数,利用Gauss-Newton法近似推导的一种二阶学习方法,具有比经典BP算法更快的收敛速度和辨识精度。

2.2 算法性能分析

(1)针对训练样本受噪声污染的实际情况,本文在常规LMSE目标函数的基础之上,通过引入一辅助约束项,构造综合目标函数,提高网络拟合曲面的光滑度,增强算法的抗噪能力。

(2)基于单新息参数修正的辨识算法,本文引入多新息理论,通过拓展新息向量,每次迭代中都可以利用遍历信息,有效克服坏数据干扰,加快算法的收敛速度。其中P值的选取根据实际输入输出数据先验信息确定。

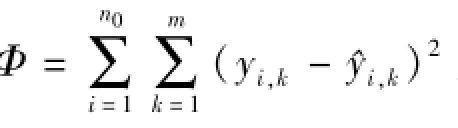
(4)基于最优化理论,本文提出的算法具有较好的收敛性能。同时得到了辨识算法的递推计算公式,可用于在线辨识,有效减小计算量。

(5)根据式(22),权值增量的递推公式可以写成

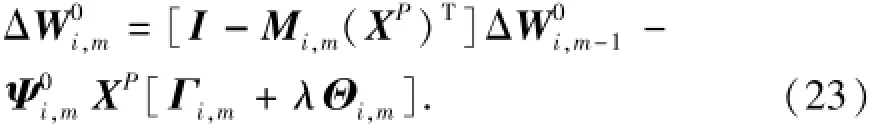
BP算法中权值增量的计算公式为

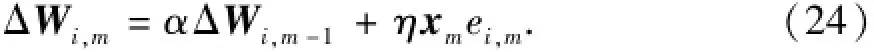
式中,α为惯性因子；η为学习速率。

将式(23)、(24)作对比可发现,式(23)也为带有惯性系数和学习因子的递推算法,它的惯性系数和学习因子都是基于多新息在线自适应调整,有效防止算法震荡,加快收敛。同时平滑算子λ的引入,增强了该辨识算法的鲁棒性,平滑网络拟合曲面。

3 仿真实验及分析

3.1 测试数据与模型评价标准

以如下典型非线性时变系统产生测试数据:

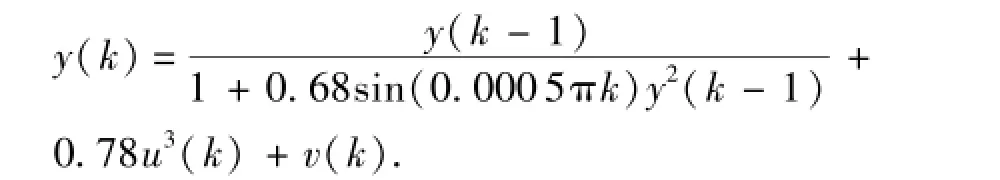
其中,输入信号u(k)=sin(0.01πk),v(k)为白噪声,通过调整白噪声v(k)的方差,得到不同噪信比的测试数据,本例噪信比δns分别设为5%,20%, 35%。P=1时,本文算法就退化为单新息的神经网络辨识算法。在不同的噪信比情况下,本文算法P分别取1和3,并与Karayiannis算法进行比较,以训练次数与均方误差作为性能评价标准。其中均方误差定义为

3.2 辨识过程与结果分析

以Matlab7.0软件为编程工具,采用三层网络结构,其中输入层为u(k)和y(k-1),一个6单元隐层及一个输出y(k),学习速率α由一维搜索确定,初始权值为0与0.01间均匀分布的随机数。不同噪信比情况下的仿真结果如图1和表1所示。为验证ω应取较大值,在P=1、噪信比δns为35%、ω分别取10和106时进行相关辨识实验,结果如图2所示。

通过对比可以发现,目标函数中辅助项的引入可以有效克服噪声的影响,同时,多新息的引入加快了辨识算法的收敛性,精度亦有所提高。当噪声污染程度较大时,算法的辨识性能明显优于Karayiannis算法。通过图2对比曲线验证,初始化=ωI,ω应取较大值(106)。仿真结果表明:基于综合目标函数的非线性神经网络多新息辨识算法在辨识精度与抗噪能力上均优于已有的Karayiannis二阶辨识算法。

图1 不同噪信比时的仿真曲线Fig.1 Simulation curves for differentnoise-to-signal ratio

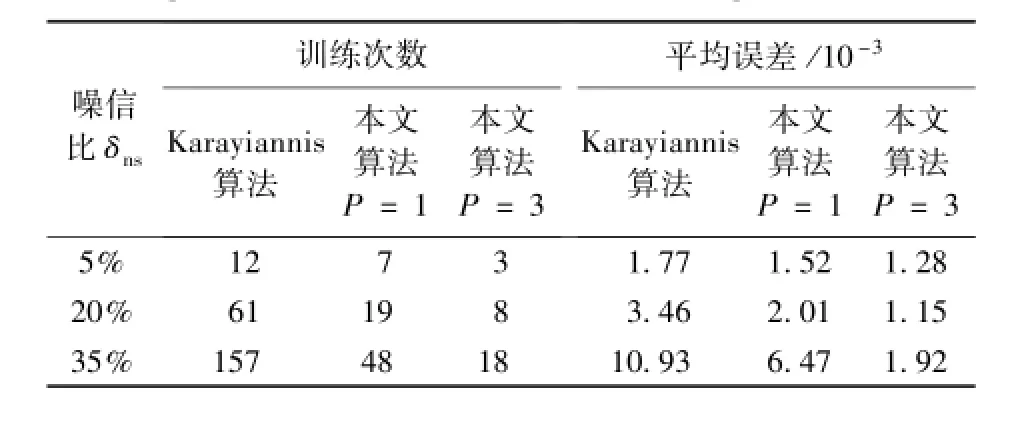
表1 不同噪信比下本文算法与Karayiannis算法仿真结果对比Table 1 Comparison of simulation results between two algorithms with different noise-to-signal ratio

图2 ω取不同值时对比仿真曲线Fig.2 Comparison curves for different ω

4 结束语

通过在目标函数中引进平滑网络输出曲面的辅助约束项,同时利用多新息参数修正,提出一种新型的非线性动态神经网络辨识算法。该算法突破了常规LMSE目标函数的限制,可有效抑制噪声对训练样本的影响,提高系统辨识的速度和精度。同时推导出算法的递推计算公式,避免矩阵求逆,可有效降低存储量和计算量。大量仿真结果表明本文算法具有鲁棒性强、收敛快速、精度高的特点,与现有的同类算法相比,更适用于非线性系统的辨识。

[1] ROJAS I,POMARES H,BERNIER J L,et al.Time series analysis using normalized PG-RBF network with regression weights[J].Neurocomputing,2002,42(1/4): 267-285.

[2] LACY S,L,BEMSTEIN D S.Subspace identification for non-linear systems with measured-input non-linearities[J]. International Journal of Control,2005,78(12):906-925.

[3] ZAPRANIS A,ALEXANDRIDIS A.model identification in wavelet neural networks framework.Proceedings of the 5th IFIP Conference on Artificial Intelligence Applications &Innovations,Thessaloniki,Greece,April 23-25,2009 [C].Berlin:Springer,2009.

[4] 华陈权,王昌明,耿艳峰,等.基于神经网络的槽式孔板湿气计量修正模型[J].中国石油大学学报:自然科学版,2009,33(6):152-156.

HUA Chen-quan,WANG Chang-ming,GENG Yan-feng, et al.Wet gas flow metering correction model of slotted orifice based on neural network[J].Journal of China U-niversity of Petroleum(Edition of Natural Science), 2009,33(6):152-156.

[5] SINGH Y P,ROYCHOWDHURY P.Dynamic tunneling based regularization in feedforward neural networks[J]. Artificial Intelligence,2001,131(1/2):55-71.

[6] KONSTANTINOS P F.Biological engineering applications of feedforward neural networks designed and parameterized by genetic algorithms[J].Neural Networks,2005,18 (7):934-950.

[7] YU J B,WANG S J,Xi L F.Evolving artificial neural networks using an improved PSO and DPSO[J].Neurocomputing,2008,71(4/6):1054-1060.

[8] 邵红梅,安凤仙.一类训练前馈神经网络的梯度算法及收敛性[J].中国石油大学学报:自然科学版,2010, 34(4):176-178.

SHAO Hong-mei,AN Feng-xian.A class of gradient algorithms with variable learning rates and convergence analysis for feedforward neural networks training[J].Journal of China University of Petroleum(Edition of Natural Science),2010,34(4):176-178.

[9] CHEN D S,RAMESH C J.A robust back propagation learning algorithm for function approximation[J].IEEE Trans on Neural Networks,1994,5(3):467-479.

[10] 徐宝昌,罗雄麟,王金山.一种基于综合目标函数的神经网络学习算法[J].中国石油大学学报:自然科学版,2009,33(6):95-99.

XU Bao-chang,LUO Xiong-lin,WANG Jin-shan.A novel neural network training algorithm based on generalized objective function[J].Journal of China University of Petroleum(Edition of Natural Science),2009,33 (6):95-99.

[11] 包芳,潘永惠.神经网络泛化性能优化算法[J].计算机工程与设计,2009,30(22):5211-5213.

BAO Fang,PAN Yong-hui.Algorithm of generalization performance optimization of neural network[J].Computer Engineering and Design,2009,30(22):5211-5213.

[12] DING F,CHEN T.Performance analysis of mlti-innovation gradient type identification methods[J].Automatica,2007,43(1):1-14.

[13] DING F,CHEN H B,LI M.Multi-innovation least squares identification methods based on the auxiliary model for MISO systems[J].Applied Mathematics and Computation,2007,187(2):658-668.

[14] 王永骥,涂健.神经元网络控制[M].北京:机械工业出版社,1999.

(编辑 修荣荣)

Multi-innovation identification algorithm of neural network based on generalized objective function

XU Bao-chang,LIU Xin-le
(College of Geophysics and Information Engineering in China University of Petroleum,Beijing 102249,China)

To improve the identification accuracy and robustness to noise of dynamic neural network learning algorithm,multi-innovation identification algorithm based on a generalized objective function was presented.The generalized function based on multi-innovation theory was constructed by combining an auxiliary constraint term with the least mean square error.The weight matrix of output layer was trained using the generalized function.The recursive equations for training weight matrix of output layer were derived using Newton iterative algorithm.Compared with the existed second-order learning algorithm,this algorithm has stronger robustness,better convergent rate and accuracy.Simulation results show the efficiency of the new algorithm.

system identification；generalized objective function；neural network；multi-innovation

TP 183

A

1673-5005(2013)02-0165-05

10.3969/j.issn.1673-5005.2013.02.027

2012-09-05

国家重大专项(2011ZX05021-003)

徐宝昌(1974-),男,副教授,博士,主要从事复杂油气系统的信息处理、建模与先进控制。E-mail:xbcyl@163.com。