能源消费碳排放零残差因素分解模型研究

宋杰鲲,窦吉芳

(中国石油大学经济管理学院,山东青岛 266580)

能源消费碳排放零残差因素分解模型研究

宋杰鲲,窦吉芳

(中国石油大学经济管理学院,山东青岛 266580)

LMDI模型、Shapley值模型和MRCI模型均是能源消费碳排放的零残差因素分解模型,对三种模型的基本形式进行拓展,提出基于多层次多因素分解的通用表述形式,给出各分解模型中因素的累积效应、逐年效应和效应贡献度的测算方法,并对三种模型特点进行对比。运用Kendall协调系数法对三种模型结果进行相容性检验,输出相容模型集；基于各相容单一分解模型,构建能源消费碳排放的最优加权组合分解模型。应用上述模型对青岛市能源消费碳排放进行分解实证,结果表明,人均GDP和人口是青岛市碳排放增加的驱动因素,能源消费强度下降和能源消费结构优化则对碳排放增长具有抑制作用。

能源管理；能源消费；碳排放；零残差；因素分解；组合分解模型

因素分解是分析能源消费碳排放变化的一种重要方法。通过因素分解,分析碳排放变化的驱动或抑制因素及其作用力强弱[1]。按照不同的分类标准,因素分解模型可以划分为多种类型[2],有无残差是判定分解模型是否科学的首要条件。目前,对数平均权重迪氏指数(LMDI)模型、Shapley值模型和平均变化率指数(MRCI)模型是科学的零残差分解方法,具有计算简便、理论基础成熟、适用广泛等优点。笔者对加法形式的LMDI模型、Shapley值模型和MRCI模型这三种分解方法的基本模型进行拓展,给出其一般形式表述,对各种模型结论进行相容性检验,据此将单一模型相组合,构建能源消费碳排放的组合分解模型；同时给出青岛市能源消费碳排放分解实证。

1 单一分解模型

1.1 LMDI模型

LMDI模型采用对数变换函数作为指标权重函数,该函数具有对称性、最大值为1、能有效处置含零参数等优点[3],自将其引入能源消费碳排放因素分解提出LMDI模型以来[4],LMDI已成为目前最常用的碳排放因素分解方法[5-7]。常见的碳排放分解因素包括GDP、人口、人均GDP、产业结构、能源消费结构、能源消费强度、碳排放系数等,按照组合形式包括三因素分解、四因素分解、五因素分解以及六因素分解等多种分解模型。如对碳排放进行六因素分解,碳排放等式如下:

式中,P、GDP/P、GDPi/GDP、Ei/GDPi、Eij/Ei、Cij/Eij分别表示人口、人均GDP、产业结构、第i产业能源消费强度、第i产业能源消费结构和碳排放系数。

不失一般性,将碳排放分解为l1+l2+l3种因素,有碳排放等式

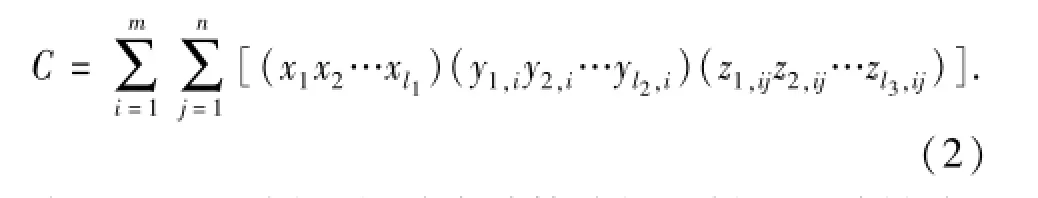
应用LMDI分解时,首先计算分解最低层的碳排放:

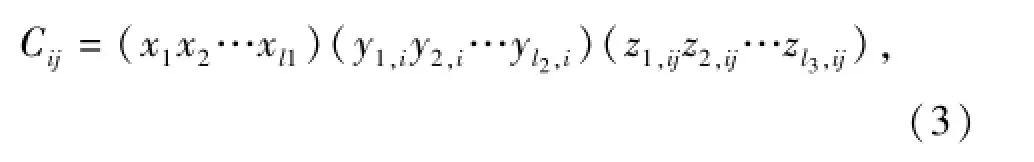
则碳排放逐年变动的LMDI分解模型为

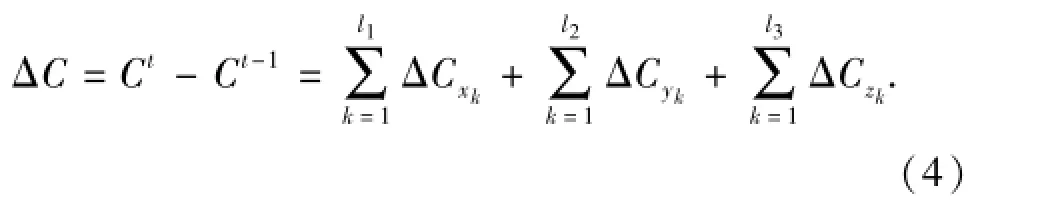
令u代表x1,…,xl1,y1,i,…,yl2,i,z1,ij,…,zl3,ij中的任一分解因素,其逐年效应为

如果存在某年度Cij或u等于0,可依据表1中的四种特殊情形结果进行选择[8]。如果考虑各因素的累积效应,则可将公式(4)～(6)及表1中的t-1换为基期0。

表1 LMDI分解的特殊情形Table 1 Special circumstances in LMDI decomposition

为了更加直观地反映各因素效应的贡献(包括对总效应的贡献率和对碳排放增加的作用力方向),定义因素效应贡献度如下:

式中,ηu为因素效应贡献度；sgn(ΔC)为碳排放量变动方向,如碳排放增加则为正,否则为负。

1.2 Shapley值模型

Shapley值分解模型[9]将碳排放分解为人口、人均GDP、能源消费强度(E/GDP)和能源利用碳排放密度(C/E)这四项因素,碳排放等式为

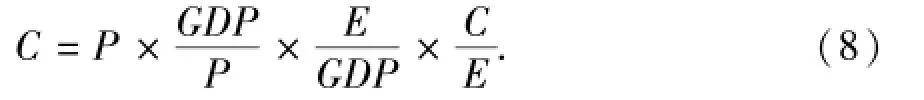
写成一般形式:

将碳排放逐年变动分解为n种因素效应,有

记所有分解因素组成局中人集合N={x1,x2,…,xn},联盟U⊆N,U≠Φ。令其特征函数

依据对称性、有效性和可加性等特征,可得局中人xi的Shapley值亦即因素xi的逐年效应为

其中,|U|为联盟U的基数亦即包含的元素个数。

将上述结论推广到式(2)所示的一般情形,得到式(4)所示的分解模型。令u代表任一分解因素,记Nij={x1,…xl1,y1,i,…yl2,i,z1,ij,…zl3,ij},对联盟U⊆Nij,U≠Φ,令其特征函数为

则有如下的各因素逐年效应测算公式:

同样地,将式(12)中的t-1换为基期0即得到各因素的累积效应,由式(7)得到各因素的效应贡献度。

1.3 MRCI模型

MRCI方法[10]以各因素平均变化率占全部因素平均变化率之和的比例为权重,是一种零残差分解方法。将式(2)的一般形式分解为模型(4),则各因素MRCI逐年效应为

式中,u代表任一因素；Aij为全部因素平均变化率之和。

同样地,将式(13)中的t-1换为基期0即得到各因素的累积效应,由式(7)得到各因素的效应贡献度。

1.4 模型对比

从模型原理和计算方法来看,三种单一分解模型均为零残差分解,但由于分解原理不同,其分解结果通常并不相同。若以最低层的碳排放变动为效应测算基准,LMDI模型以各因素对数值变化占全部因素对数值变化之和的比例为权重,MRCI模型则以各因素平均变化率占全部因素平均变化率之和的比例为权重。比较而言,MRCI模型更加易于理解,但其存在两方面不足:一是以各因素相邻年度数值的算术平均值或考察年度与基期数值的算术平均值为基础测算平均变化率,缺乏严密的理论支撑；二是不同因素的平均变化率有正有负,理论上存在全部因素平均变化率之和Aij为0的可能,导致该方法失效。LMDI模型尽管缺乏很好的经济含义,但其采用的对数变换函数具有介乎几何平均值和算术平均值之间的良好数学性质[11]:

有效提高了平均碳排放的可解释性。Shapley模型实质上求得的是各局中人对其可以参与的所有联盟的平均边际贡献,在满足个体合理性和群体合理性的合作博弈分配方面具有明确的经济含义[12],但在碳排放分解方面,由于不同因素对其参与联盟的碳排放变动并无一致的作用方向,导致联盟不具有稳定性,一定程度上削弱了模型的可解释性。

2 组合分解模型

2.1 相容性检验

不同的分解方法有着各自的理论基础,通常上述三种模型均适用于能源消费碳排放因素分解,但可能存在分解结论差别较大的情形,引入Kendall协调系数法对三种模型进行相容性检验[13]。记第k种模型中第r种因素第t年的效应为ΔCkrt,效应贡献度为ηkrt,k=1,2, 3；r=1,2,…,l1+l2+l3；t=1,2,…,T,对第k种模型中的所有ηkrt值由小到大进行排序,数值越小表明对碳排放增加的抑制作用越强,给出相应的排序值pkrt,pkrt∈{1,2,…,T(l1+l2+ l3)},不同的分解模型中排序值通常应基本一致。计算统计量

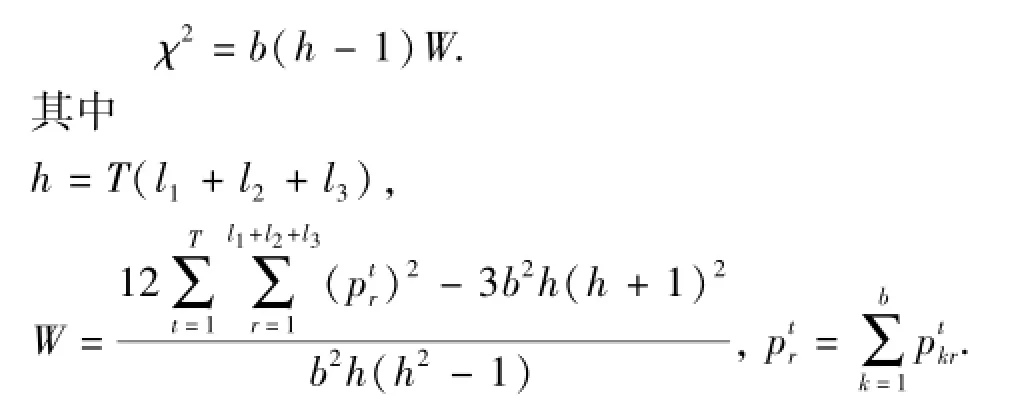
式中,b为单一分解模型个数,b= 3；h为排序值个数；W为协调系数,用以辨识实际排序结果与最大可能排序结果之间的分歧程度。

统计量χ2近似服从χα2(h-1),给定显著性水平α,如果χ2≥χα2(h-1),则判定b种方法相容,否则不相容,需逐一剔除其中的模型,对其余模型进行相容性检验,最终输出包含z种单一模型的相容模型集。

2.2 组合分解

为了充分利用z种相容模型所蕴含的信息,采用最优加权组合模型对所有相容单一模型进行组合[14],构建组合分解模型。记第k种模型的权重为wk,则第r种因素第t年的效应组合值为以最小化所有因素各年度效应组合值与每一种模型相应效应值的误差平方和为目标,构建最优加权组合分解模型:

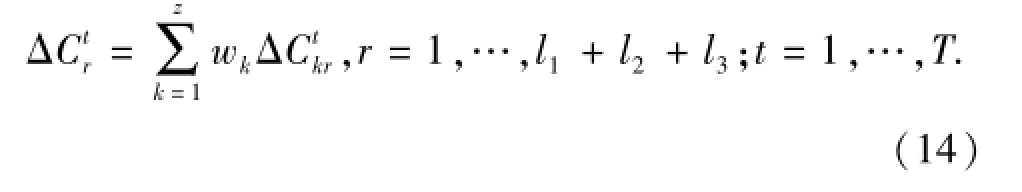
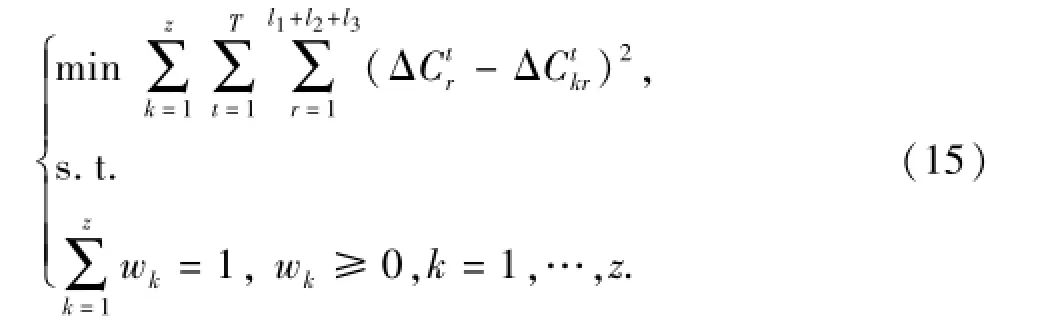
求解得到各单一分解模型的权重,代入式(14)即得各因素的组合效应值。由式(7)得到各因素的组合效应贡献度。

3 实例分析

对青岛市2000—2009年能源消费碳排放进行因素分解,首先按照文献[8]测算的各种能源的折标准煤系数和碳排放系数计算历年碳排放量,其中能源消费量(实物量)数据来自2001—2010年《青岛统计年鉴》,得到碳排放结果如表2所示。

表2 2000—2009年青岛市能源消费碳排放量Table 2 Carbon emissions from energy consumption of Qingdao in the year of 2000-2009

将碳排放分解为人口(P)、人均GDP(g)、能源消费强度(E/GDP,记为e)、能源消费结构(Ej/E,记为sj)以及碳排放系数(Cj/Ej,记为cj),有碳排放等式

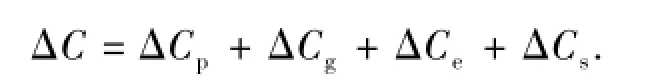
由于各能源碳排放系数基本保持不变,将碳排放变化ΔC分解为人口效应ΔCp、人均GDP效应ΔCg、能源消费强度效应ΔCe和能源消费结构效应ΔCs,即运用LMDI模型、Shapley值模型和MRCI模型计算各因素逐年效应、累积效应及效应贡献度,结果分别见表3、表4和表5,其中括号内数值为对应的效应贡献度。可见,三种模型的分解结果有所差异,特别是2005—2009年在能源消费强度效应和能源消费结构效应方面,LMDI模型与另外两种模型之间的差异较大。

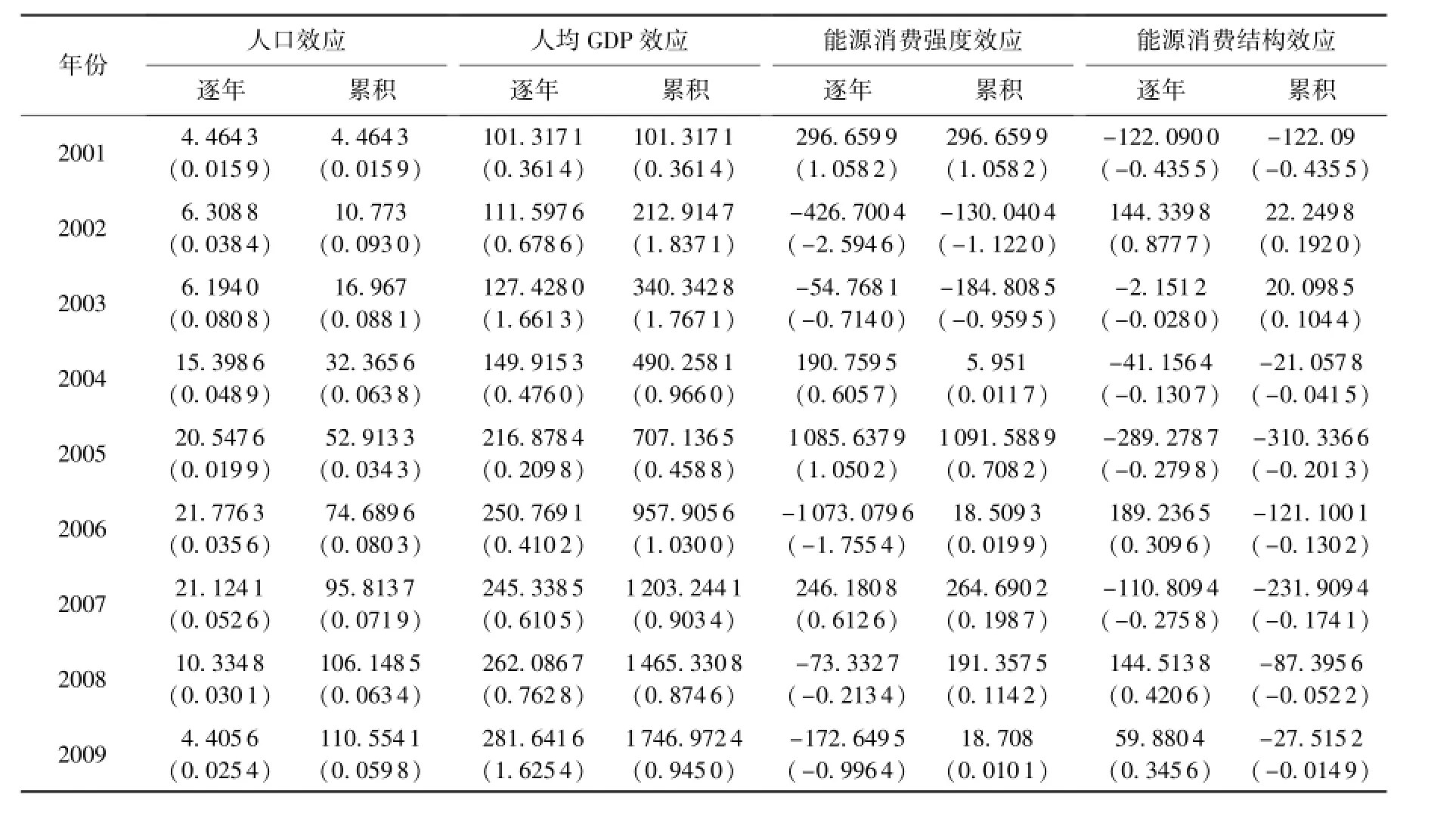
表3 LMDI模型的各因素效应Table 3 Effect of different factor by LMDI model104t

表4 Shapley值模型的各因素效应Table 4 Effect of different factor by Shapley value model104t

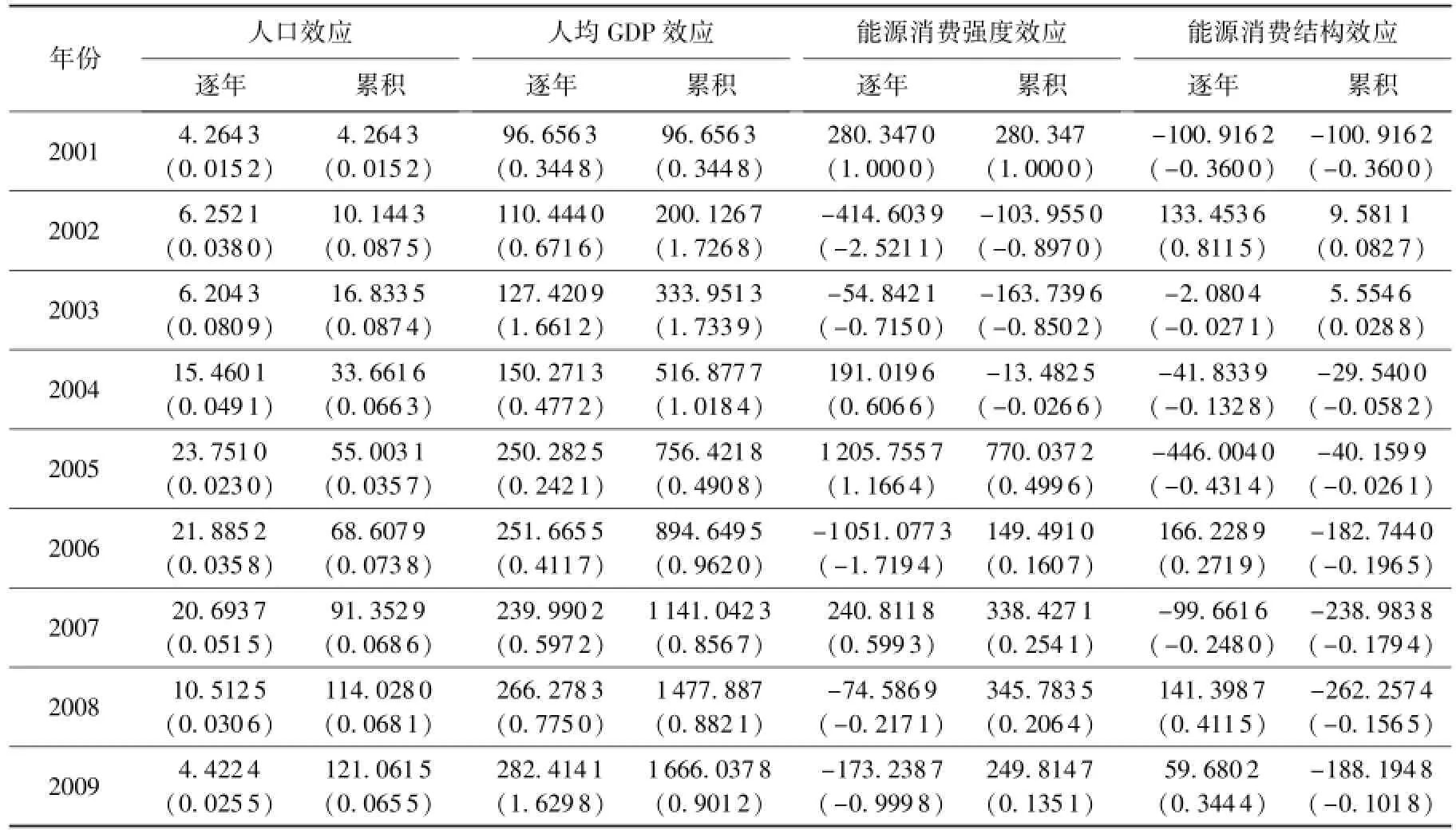
表5 MRCI模型的各因素效应Table 5 Effect of different factor by MRCI model104t

应用Kendall协调系数法对三种模型的效应贡献度进行相容性检验,得到逐年效应的协调系数W =0.9992,统计量χ2=104. 9159；累积效应的协调系数W=0.975 1,统计量χ2=102.381 4。给定显著性水平α=0.01,χα2(35)=57.3421,可见,三种模型的逐年效应和累积效应均通过相容性检验。

基于三种单一分解模型结果,构建式(15)的最优加权组合分解模型,求解得到LMDI模型、Shapley值模型和MRCI模型的逐年效应最优权重均为1/3,累积效应最优权重分别为0.333 334、0.333 334和0.333332,代入式(14)得到各因素逐年效应和累积效应结果见表6。2009年各因素累积效应贡献度、2001—2009年各因素逐年效应贡献度见图1和图2。

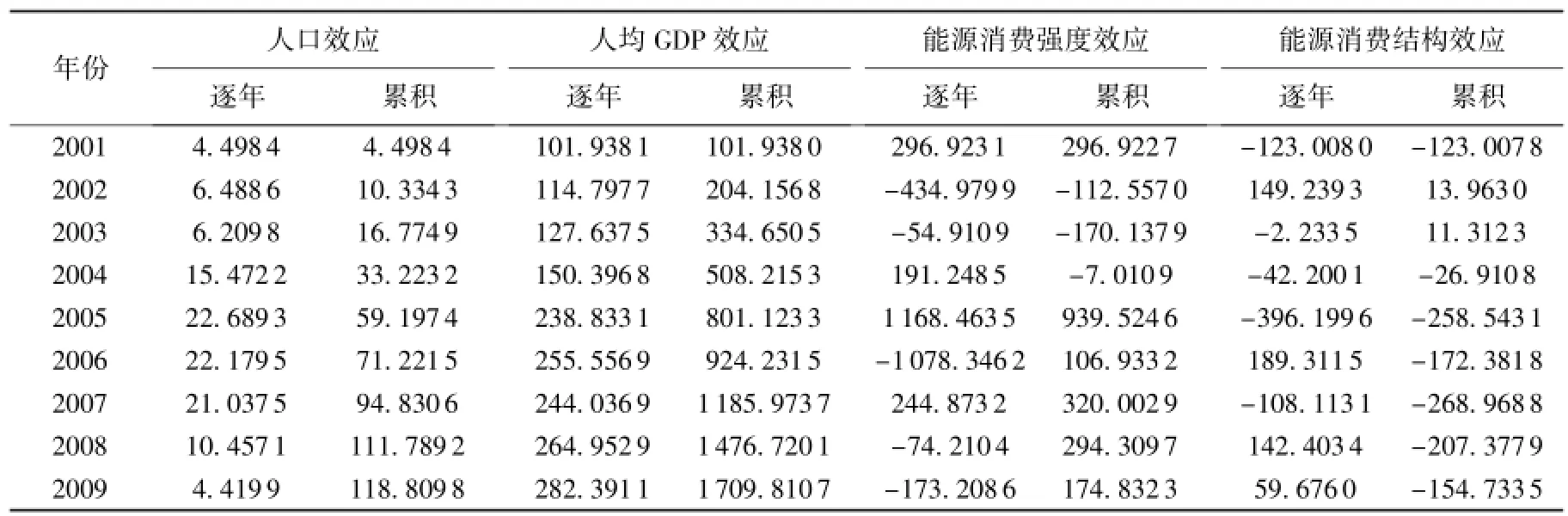
表6 组合分解模型的各因素效应Table 6 Effect of different factor by combination decomposition model104t

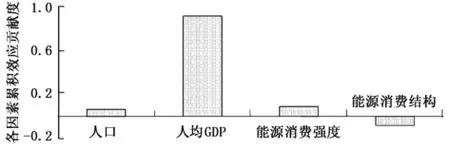
图1 2009年各因素累积效应贡献度Fig.1 Accumulated effect contribution of different factor in the year of 2009

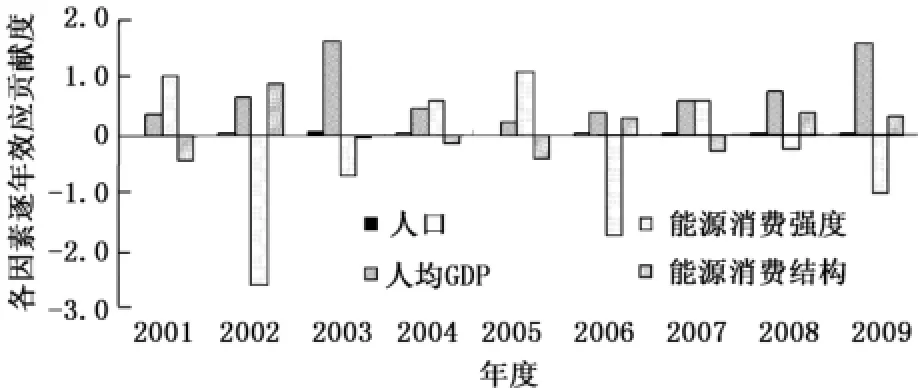
图2 2001—2009年各因素逐年效应贡献度Fig.2 Year after year effect contribution of different factor in the year of 2001—2009

可见,以2000年为基期,2009年青岛市人均GDP和人口的累积效应、2001—2009年的逐年效应均为正值,这表明近年来青岛市人均GDP和人口对碳排放增加具有拉动作用。其中人均GDP累积效应贡献度高达0.9248,是碳排放增加的最主要拉动因素；人口效应累积贡献度为0.064 3,对碳排放量增加具有较弱的拉动作用。2009年能源消费强度的累积效应贡献度为0.094 6,但2001—2009年的逐年效应有所波动,2001年、2004—2005年和2007年为正值,2002—2003年、2006年、2008—2009年为负值,这与青岛市2008年以来不断提高能源利用效率,能源消费强度明显下降有关。青岛市2007年能源消费强度为0.131 5 kg(标准煤)/元,2008年、2009年分别降至0.127 2 kg(标准煤)/元和0.118 7 kg(标准煤)/元,今后青岛市应继续强化节能减排,严格落实能源消费强度目标制度,扩大能源消费强度下降导致的负向效应,抑制碳排放增长。2009年青岛市能源消费结构的累积效应贡献度为-0.0837,但其逐年效应也有一定波动。2001年、2003—2005年和2007年为负值,2002年、2008—2009年为正值,这与青岛市近年来油品消费比例大幅上升而原煤和焦炭消费比例下降很小有着一定关系。2007年青岛市油品消费比例、原煤和焦炭消费比例分别为12.62%、25.36%,2008年、2009年油品消费比例分别升至27.10%和37.19%,而原煤和焦炭消费比例仅分别降至28.86%和26.14%。这表明青岛市今后应注重能源消费结构优化,进一步降低原煤和焦炭消费比例,使能源消费结构逐年效应调整为负值,不断提高能源消费结构优化对碳排放增加的抑制作用。

4 结 论

(1)对LMDI模型、Shapley值模型和MRCI模型这三种零残差因素分解模型的加法形式进行扩展,提出基于多层次多因素分解的三种模型的通用表述形式,分别给出其因素累积效应和逐年效应计算公式,并定义了同时反映因素效应贡献率大小和作用力方向的因素效应贡献度。同时,从模型原理和可解释性角度对三种模型进行对比分析。

(2)鉴于三种单一分解模型结论可能存在较大的差异,提出运用Kendall协调系数法进行模型相容性检验,形成相容模型集。对于相容的单一模型,构建最优加权组合分解模型,实现各单一模型的信息融合,提高分解结论的客观性。

(3)给出青岛市能源消费碳排放分解实证,验证基于单一分解模型的组合分解的可行性与有效性。同时,研究结果表明,人均GDP是青岛市碳排放增加的最主要拉动因素,人口具有较弱的拉动作用,能源消费强度下降和能源消费结构优化对碳排放增加具有较为明显的抑制作用。

[1]宋杰鲲.基于支持向量回归机的中国碳排放预测模型[J].中国石油大学学报:自然科学版,2012,36(1): 127-135.

SONG Jie-kun.Chinaıs carbon emissions prediction model based on support vector regression[J].Journal of China U-niversity of Petroleum(Edition of Natural Science),2012, 36(1):182-187.

[2]ANG B W,LIU F L,CHEW E P.Perfect decomposition techniques in energy and environmental analysis[J].Energy Policy,2003,31:1561-1566.

[3]SATO K.The ideal log-change index number[J].The Review of Economics and Statistics,1976,58(2):223-228.

[4]ANG B W,CHOI K.Decomposition of aggregate energy and gas emission intensities for industry:a refined divisia index method[J].The Energy Journal,1997,18(3):59-73.

[5]WU L,KANEKO S,MATSUOKA S.Driving forces behind the stagnancy of Chinaıs energy-related CO2emissions from 1996 to 1999:the relative importance of structural change, intensity change and scale change[J].Energy Policy, 2005,33:319-335.

[6]徐国泉,刘则渊,姜照华.中国碳排放的因素分解模型及实证分析:1995—2004[J].中国人口资源与环境, 2006,16(6):158-161.

XU Guo-quan,LIU Ze-yuan,JIANG Zhao-hua.Decomposition model and empirical study of carbon emissions for China,1995-2004[J].China Population,Resources and Environment,2006,16(6):158-161.

[7]朱勤,彭希哲,陆志明,等.中国能源消费碳排放变化的因素分解及实证分析[J].资源科学,2009,31(12): 2072-2079.

ZHU Qin,PENG Xi-zhe,LU Zhi-ming,et al.Factors decomposition and empirical analysis of variations in energy carbon emission in China[J].Resources Science,2009, 31(12):2072-2079.

[8]宋杰鲲.基于LMDI的山东省能源消费碳排放因素分解[J].资源科学,2012,34(1):35-41.

SONG Jie-kun.Factor decomposition of carbon emissions from energy consumption of Shandong province based on LMDI[J].Resources Science,2012,34(1):35-41.

[9]ALBRECHT J,FRANCOIS D,SCHOORS K.A Shapley decomposition of carbon emissions without residuals[J]. Energy Policy,2002,30:727-736.

[10]CHUNG H S,RHEE H C.A residual-free decomposition of the sources of carbon dioxide emissions:a case of the Korean industries[J].Energy,2001,26:15-30.

[11]TORNQVIST L,VARTIA P,VARTIA Y.How should relative changes be measured?[J].The America Statistician,1985,39(1):43-46.

[12]汪贤裕,肖玉明.博弈论及其应用[M].北京:科学出版社,2008:172-215.

[13]陈国宏,李美娟,陈衍泰.组合评价及其计算机集成系统研究[M].北京:清华大学出版社,2007.

[14]梁伟,张来斌,胡瑾秋,等.动态环境下燃压机组的自适应安全评估方法[J].中国石油大学学报:自然科学版,2012,36(1):127-135.

LIANG Wei,ZHANG Lai-bin,HU Jin-qiu,et al.Self-adaptive safety assessment method for gas-turbine/compressor unit in dynamic environment[J].Journal of China U-niversity of Petroleum(Edition of Natural Science),2012, 36(1):127-135.

(编辑 修荣荣)

Zero-residual factor decomposition models of carbon emissions from energy consumption

SONG Jie-kun,DOU Ji-fang
(School of Economics and Management in China University of Petroleum,Qingdao 266580,China)

LMDI model,Shapley value model and MRCI model are all zero-residual factor decomposition models of carbon emissions from energy consumption.The three basic forms of decomposition models were expanded,and their general forms based on multiple levels and multiple factors were proposed.The calculation methods of accumulation effect,year after year effect and effect contribution of different factor were provided respectively.Meanwhile,the characteristics of three models were compared.Kendall coordination coefficient method was employed for compatibility test on different modelsı results,and the compatible model set can be output.Based on compatible single decomposition models,an optimal weighted combination decomposition model of carbon emissions from energy consumption was constructed.The above models were applied to make an empirical analysis on factor decomposition of carbon emissions from energy consumption of Qingdao city.The results show that per capita GDP and population are the driving factors of carbon emissions,while reducing energy consumption intensity and optimizing energy consumption structure have inhibition role on the growth of carbon emissions.

energy management；energy consumption；carbon emissions；zero-residual；factor decomposition；combination decomposition model

X 32

A

1673-5005(2013)01-0183-07

10.3969/j.issn.1673-5005.2013.01.032

2012-06-20

山东省自然科学基金项目(ZR2011GQ004)；中央高校基本科研业务费专项资金资助项目(10CX04012B,11CX04034B)；教育部人文社会科学研究青年基金项目(10YJC630207)；山东省高校人文社会科学研究计划项目(J10WG94)；大学生创新创业训练计划创新训练项目(111042555)

宋杰鲲(1979-),男,副教授,博士,从事能源经济管理方面的研究。E-mail:songjiekun@163.com。