页岩气藏运移机制及数值模拟
2013-07-07樊冬艳黄朝琴孙致学张国浩
姚 军,孙 海,樊冬艳,黄朝琴,孙致学,张国浩
(中国石油大学石油工程学院,山东青岛 266580)
页岩气藏运移机制及数值模拟
姚 军,孙 海,樊冬艳,黄朝琴,孙致学,张国浩
(中国石油大学石油工程学院,山东青岛 266580)
基于双重连续介质,采用尘气模型(DGM)建立基岩和裂缝运动方程,基岩中考虑气体在基岩孔隙中黏性流、Knudsen扩散、分子扩散以及气体在基岩孔隙表面的吸附解吸,吸附采用Langmuir等温吸附方程;裂缝中考虑黏性流、Knudesen扩散和分子扩散机制,在此基础上建立基岩-裂缝双重介质数值模型并采用有限元方法对模型进行求解。根据数值模拟结果对影响页岩气藏产能的因素进行分析。结果表明:页岩气产出气是游离气和吸附气解吸共同采出的结果,在给定的页岩气藏条件下,游离气影响更大,吸附对页岩气产能有较大影响,忽略吸附会导致预测产能偏低;Knudsen扩散(或Klinkenberg效应)对基岩视渗透率影响较大,越靠近生产井,Knudsen扩散和Klinkenberg效应的影响越大,基岩视渗透率随生产时间延长变大;裂缝渗透率越大,页岩气产量越大,基岩渗透率对页岩气产能影响不大。
油藏;页岩气;双重介质;尘气模型;吸附;有限元法;运移机制;数值模拟
随着油气开采技术的提高及资源需求量的增加,页岩气藏因其资源丰富、潜力巨大成为研究的热点[1-3]。页岩气藏孔隙直径一般为纳米级,赋存方式多样(吸附气和游离气),孔隙度、渗透率极低,页岩基岩是超低孔超低渗的致密多孔介质[4-6]。气体在致密多孔介质中的运移是多重机制(黏性流、分子扩散、Knudsen扩散及吸附气解吸)共同作用的结果[7],常规的达西流动方程难以准确描述气体在致密多孔介质中的运移规律。由于大部分页岩气藏天然裂缝发育,多采用双重介质模型对页岩气藏进行数值模拟研究,但目前页岩气藏数值模型未全面考虑气体在页岩气藏中的运移传输机制[8-11]。笔者建立页岩气双重介质数值模型,全面考虑气体在页岩气藏中运移传输机制,采用有限元方法对模型求解,分析不同参数对页岩气藏产能的影响。
1 页岩气双重介质模型
假设:页岩气藏天然裂缝发育,气体以游离态存储于天然裂缝,基岩中游离态和吸附态的气并存;页岩气藏中仅存在单相单组分气体运移;气藏在生产过程中温度保持不变,气体在基岩表面满足Langmuir等温吸附方程。
1.1 页岩气基岩运动方程
等温条件下,气体在多孔介质中的质量传输有以下几种机制:黏性流、Knudsen扩散、分子扩散(若有气体吸附在多孔介质表面还存在吸附气的解吸)。一般用Knudsen数来表示连续模型适宜程度,以此来判断流体在多孔介质中的运移传输机制,Knudsen数是气体平均自由程与孔隙直径的比值。
1.1.1 黏性流
当气体平均运动自由程小于孔隙直径(Knudsen数远小于1)时气体分子的运动主要受分子间碰撞支配,分子与壁面的碰撞较少。此时单组分气体之间存在压力梯度所引起的黏性流,黏性流的质量传输可以用达西定律[12]表示为

式中,Nv为黏性流引起的质量流量,kg/(m2·s);kmi为基岩的本征渗透率,m2;pm为基岩压力,Pa;ρm为基岩气体的密度,kg/m3;μg为气体黏度,Pa·s。
1.1.2 Knudsen扩散
当孔隙直径很小时,气体的平均自由程与孔隙直径相近(Knudsen数大于1),这时气体分子与壁面之间的碰撞比分子之间的碰撞占支配作用,此时气体之间的质量流量可以用Knudsen扩散[12]表示为

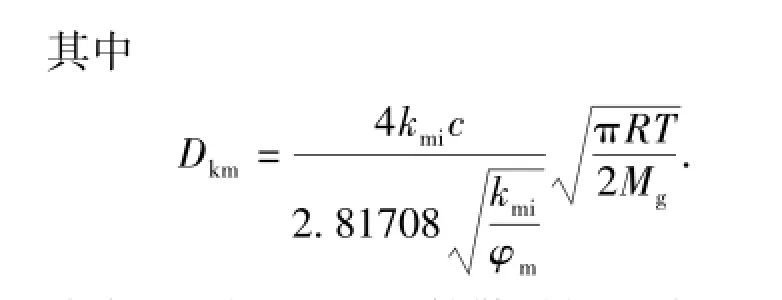
式中,Nk为Knudsen扩散引起的质量流量,kg/(m2· s);Cm为气体的摩尔浓度,mol/m3;Mg为气体的摩尔质量,kg/mol;Dkm为基岩的扩散系数[13],m2/s; φm为基岩孔隙度;R为理想气体分数;Z为气体压缩因子;T为温度,K;c为趋近于1的常数[11],在本文中取1。
1.1.3 分子扩散
当气体平均运动自由程小于孔隙直径(Knudsen数小于1),若多孔介质中气体为混合物,由于气体混合物分子质量的不同,导致混合物气体存在不同分子速度,此时多孔介质中存在气体混合物浓度梯度引起的质量传输,用分子扩散表示此种情况下的质量传输,用菲克定律表示气体分子扩散质量。两组分混合物由分子扩散引起的质量流量为

式中,NA为组分A因分子扩散引起的质量流量, kg/(m2·s);ωA为组分A的质量分数;D*AB为气体在多孔介质中有效分子扩散系数[14],m2/s;Sg为气体饱和度;τ为多孔介质的迂曲度;MA和MB分别为气体A和气体B的摩尔质量,kg/mol;p为压力,Pa;σ为气体分子的Lennard-Jones势能碰撞直径,Å;Ω为分子常数。
1.1.4 等温吸附方程

吸附气一般吸附在页岩的基岩表面,页岩吸附符合Langmuir等温吸附式[15],式中,qads为页岩单位面积的吸附量,kg/m3;Vstd为标准状况(0℃,101.325 kPa)下的摩尔体积,m3/mol; qstd为标准状况下页岩单位质量的吸附体积,m3/kg; VL为Langmuir体积,m3/kg;pL为Langmuir压力,Pa; ρs为页岩岩心密度,kg/m3。
1.1.5 页岩气基岩运动方程的建立
根据Javadpour[4]对页岩基岩孔隙Knudsen数的研究,在页岩基岩孔隙尺寸和压力下,Knudsen数处于黏性流、Knudsen扩散和分子扩散的过渡区域,此时气体在基岩孔隙中质量传输是黏性流、Knudsen扩散、分子扩散以及气体解吸的共同作用。一般采用ADM(advective-diffusive model)和DGM(dusty gas model)[16]来建立气体在多孔介质中分子扩散、黏性流以及Knudsen扩散的混合机制, ADM只是黏性流项和扩散项的简单线性相加,DGM是采用气体动力学建立的考虑黏性流与扩散相互影响耦合机制。在双组分模型中,低压高渗情况下,两个模型结果差别不大,高压低渗情况下两个模型差别较大[16]。因此,在页岩基岩超致密多孔介质中,本文中采用DGM来建立气体在页岩基岩中运动方程:

式中,FA为多孔介质中双组分气体组分A的总的质量流量;DkA为组分A的Knudsen扩散系数;xA为组分A的摩尔分数。本文中考虑气体为单组分,单组分可以假设为特殊双组分混合物(xA=1),可得页岩气为单组分气时基岩运动方程为
式中,Fm为基岩气体的质量流量,kg/(m2·s)。
为了比较ADM和DGM在单组分气体运移时运动方程,采用ADM建立页岩气基岩运动方程为
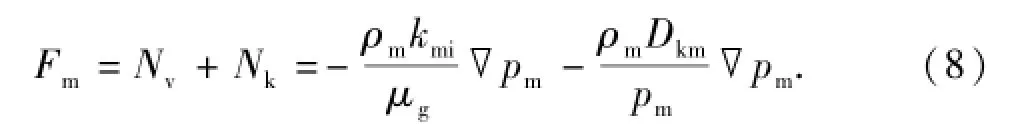
比较式(7)和式(8)发现,单组分情况下DGM与ADM所建运动方程相同。式(8)可表示为
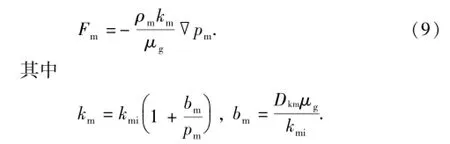
式中,km为基岩视渗透率,m2;bm为气体在基岩中的Klinkenberg系数.由式(10)可知,气体在多孔介质中的Klinkenberg效应是由气体在多孔介质中Knudsen扩散引起的,多孔介质越致密,Knudsen扩散影响越大,Klinkenberg效应越大。
1.2 页岩气裂缝运动方程
页岩裂缝中考虑气体在黏性流机制、Knudsen扩散以及分子扩散,与基岩的运动方程的推导过程类似,可得页岩气裂缝中运动方程为
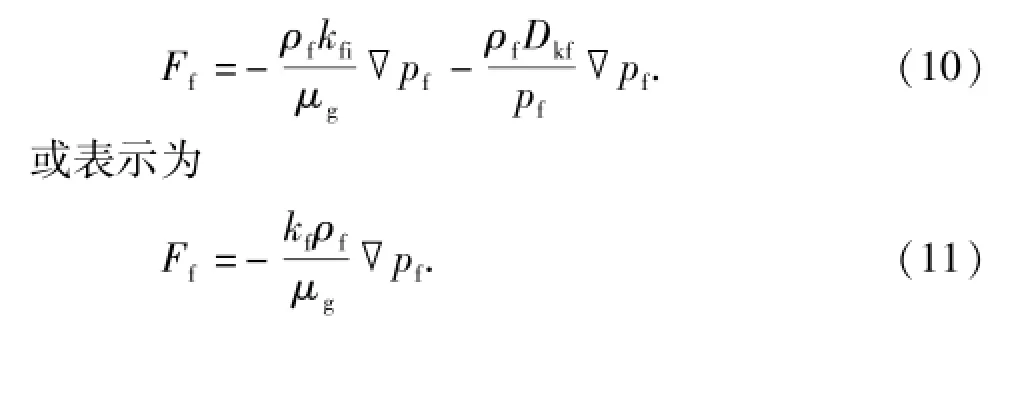

式中,Ff为气体在裂缝中质量流量,kg/(m2·s);ρf为气体在裂缝中密度,kg/m3;pf为裂缝压力,Pa;kfi为裂缝本征渗透率,m2;kf为裂缝视渗透率,m2;bf为裂缝中的Klinkenberg系数;Dkf为裂缝中的Knudsen扩散系数,m2/s;φf为裂缝孔隙度。
1.3 连续性方程
建立双重介质模型模拟页岩气的生产状况,基岩存在吸附气和游离气,裂缝中仅存在游离气,基岩中考虑黏性流、Knudsen扩散、分子扩散以及解吸机制,裂缝中考虑黏性流、Knudsen扩散机制、分子扩散机制,分别得到基岩和裂缝的连续性方程。

1.3.1 基岩连续性方程Qp表示裂缝和基岩的窜流量[17]:

式中,α*为窜流系数[17];Lx和Ly分别为x和y方向的裂缝间距。
将式(7)和式(11)带入式(12)得:


1.3.2 裂缝连续性方程

1.4 数学模型
由页岩气基岩和裂缝的运动方程以及连续性方程,可得页岩气裂缝-基岩双重介质数学模型为
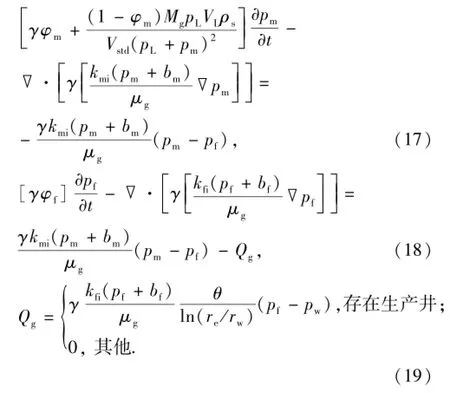
初始条件:

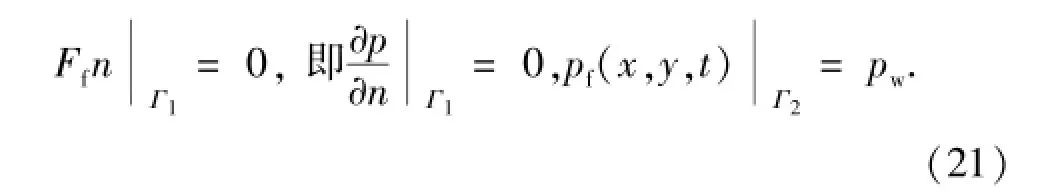
2 模型求解
边界条件:设Γ=Γ1+Γ2表示求解区域的边界,Γ1表示外边界,Γ2表示内边界,假设外边界封闭内边界定压,则边界条件为
对方程(17)~(21)采用有限元方法进行求解[19-20],求解时裂缝压力pf与基岩压力pm交替求解,先求pf后求pm。采用隐式裂缝压力pf显式基岩压力pm,先对时间域按向前差分进行离散,然后由式(17)~(19)得到n+1时刻的裂缝压力值为

利用标准伽辽金方法推导有限元的积分弱形式,首先采用三角形单元剖分,选取单元形函数,则任一点的压力可以近似为

式中,Ne=[N1,N2,N3]为单元的形函数;pf,e= [pf,1,pf,2,pf,3]为裂缝系统该单元节点处的压力值。又因为外边界封闭,则对式(22)两边在单元内进行积分,利用Guass部分积分公式可得到单元的特性矩阵为

把单元矩阵和列阵组合得到油藏的整体矩阵和列阵,油藏节点总数为Np。方程组可写为

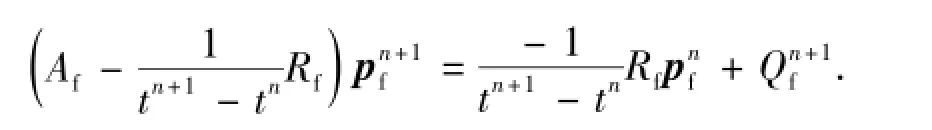
则裂缝系统相应的有限元支配方程为
其中

采用Newton-Raphson方法迭代交替求解式(25)和式(27)可以得到任意时刻的裂缝系统和基岩系统的压力值。
3 实例计算及影响因素
为了研究页岩气藏双重介质模型,模拟井距为400 m的一口生产井的生产动态[9-10](图1),由于井网对称性,只计算左下角1/4区域的生产动态。基本参数如下:气藏初始压力为10.4 MPa,定压生产,井底压力为3.45 MPa,初始气藏温度323.14 K,气体组分为CH4,基岩本征渗透率0.0001×10-3μm2,基岩孔隙度为0.05,裂缝间距0.20 m(由文献[9]知页岩裂缝间距为0.05~10 m),裂缝孔隙度为0.001,裂缝本征渗透率为1×10-3μm2,Langmuir体积为2.831 7×10-3m3/kg,Langmuir压力为10.4 MPa,页岩密度为2 600 kg/m3,甲烷摩尔质量为0.016 kg/mol,气体压缩因子为1,标准状况下摩尔体积为0.0224 m3/mol,井筒半径为0.1 m。

图1 页岩气生产区域示意图Fig.1 Segment figure of shale gas production
3.1 吸附对页岩气产能的影响
图2表示页岩气生产过程中吸附气和游离气对日产气量和累积产气量的贡献,从累积产量和日产气量来看,页岩气的产能主要来源于游离气,但是吸附气解吸也占较大的比例,页岩气产能是游离气生产和吸附气解吸共同作用的结果。由日产气量随时间的变化来看,页岩气有较长时间的稳产期,到后期生产速度减慢。

图2 吸附气和游离气对页岩气产能的贡献Fig.2 Contribution of free gas and adsorped gas to shale gas production
图3为模型中考了吸附和不考虑吸附的日产气量和累积产气量随时间的变化,比较考虑吸附和不考虑吸附的两个模型计算的日产气量和累积产气量,生产初期两个模型计算的累积产气量和日产气量差别不是很大,生产中后期差别变大,这是由于生产初期游离气对产能的贡献更大,随时间增加吸附气的贡献增大。从总的累积产气量来看,吸附对页岩气产能有较大的影响,页岩气生产过程中不能忽略吸附的影响。
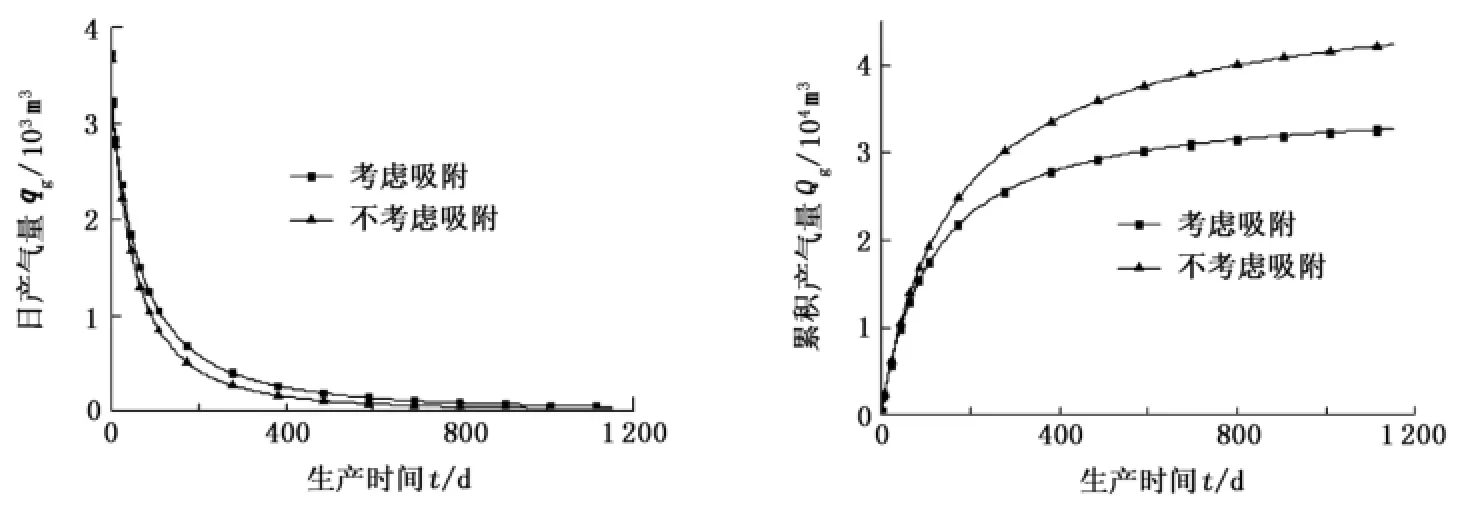
图3 吸附对页岩气产能的影响Fig.3 Effect of adsorption on shale gas production
3.2 基岩和裂缝系统视渗透率动态变化
图4为井点对角线上5个点基岩视渗透率与初始基岩本征渗透率的比值随时间的变化及平均视渗透率与本征渗透率的比值随时间的变化曲线。由图4可知,视渗透率的比值随时间越来越大,而且比值为1.2~5.0。由式(3)可知,基岩视渗透率和基岩本征渗透率的比值反映了生产过程中Knudsen扩散对整个基岩气体质量传输量的贡献程度,比值接近于1,说明Knudsen扩散对基岩传输影响不大,比值远大于1,说明Knudsen扩散对基岩传输的影响很大;随着生产时间的增加,基岩孔隙压力下降,此时基岩中黏性流传输量减小,而Knudsen扩散传输量变化不大,因此基岩视渗透率和基岩本征渗透率比值随生产时间的增加逐渐增加,说明生产时间越长, Knudsen扩散对基岩传输量的贡献越大。因此,基岩的Knudsen扩散(或Klinkenberg效应)对基岩渗透率影响较大;越靠近井点,渗透率比值越大,生产井附近基岩的Knudsen扩散的影响最大。

图4 基岩视渗透率随时间的变化Fig.4 Variation of matrix apparent permeability with time
图5为裂缝视渗透率与初始裂缝本征渗透率的比值随时间的变化曲线。与图4基岩视渗透率比值相比,裂缝视渗透率随时间变化不大,视渗透率的比值为1.000 3~1.003,说明Knudsen扩散(或Klinkenberg效应)对裂缝视渗透率影响不大,这是因为相比较于基岩系统,裂缝系统的孔隙直径很大,此时气体的平均自由程远小于孔隙直径,此时在裂缝系统中气体传输以黏性流为主,Knudsen扩散对裂缝系统的传输量影响不大。
3.3 基岩和裂缝渗透率对页岩气产能的影响
图6为不同基岩本征渗透率下页岩气累积产量和日产量随时间的变化曲线。由图6可知,页岩基岩渗透率越大,页岩日产气量和累积产气量越大;基岩渗透率越小,基岩渗透率对页岩气藏产能的影响越小,这是由于基岩渗透率越小,基岩渗透率和裂缝渗透率的差别越大,此时裂缝系统是主要的渗流通道,因此基岩对生产速度的影响越小。
图7为不同裂缝本征渗透率下页岩气累积产量和日产量随时间变化的曲线。由图7可知,裂缝渗透率越大,日产量越大,稳产期越短,日产量下降的越早;反之裂缝渗透率越小,生产初期日产量较小,稳产期越长;但是从累积产量来看,裂缝渗透率越大,累积产量越大,裂缝渗透率小于5×10-3μm2,不同裂缝渗透率累积产量的差别较大,当裂缝渗透率大于5×10-3μm2时,裂缝渗透率对累积产量的影响变小,生产后期累积产量已相差不大。
对比基岩和裂缝渗透率对页岩气产能的影响,裂缝渗透率对产能有较大的影响,基岩渗透率对产能影响相对较小。

图5 裂缝视渗透率随时间变化Fig.5 Variation of fracture apparent permeability with time

图6 基岩渗透率对页岩气产能的影响Fig.6 Effect of matrix permeability on shale gas production
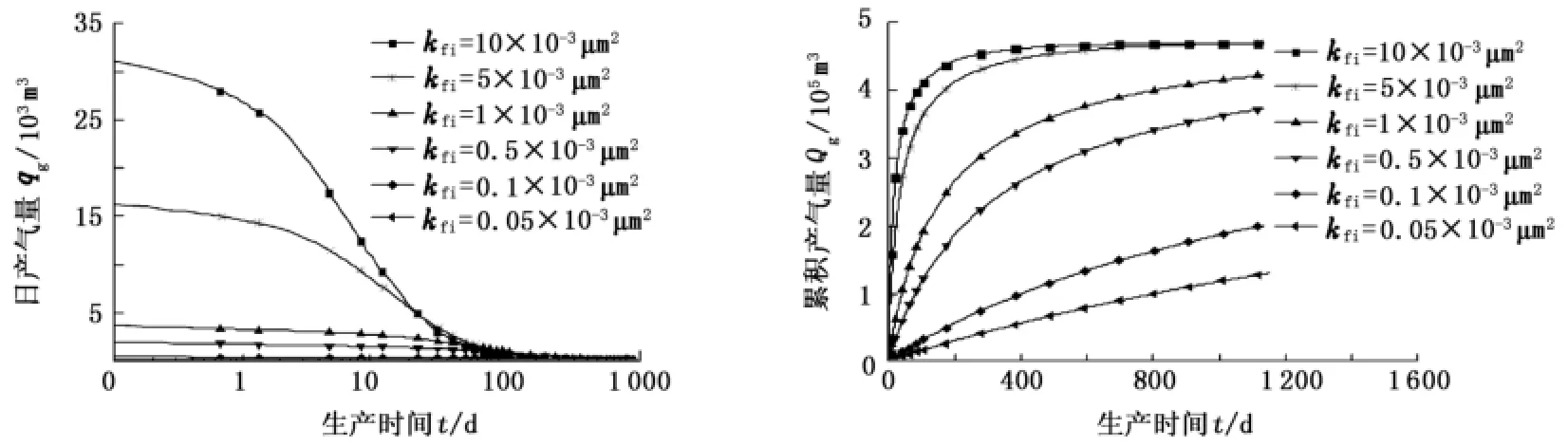
图7 裂缝渗透率对页岩气产能的影响Fig.7 Effect of fracture permeability on shale gas production
4 结 论
(1)页岩产出气体既存在游离气又有解吸气,游离气占得比例最大,解吸气也占较大比例。不考虑吸附会导致模型预测产气量变少,模型中不应忽略吸附的影响。
(2)生产过程中,基岩视渗透率变化较大,裂缝视渗透率变化较小,Klinkenberg效应和Knudsen扩散对基岩视渗透率具有较大影响,生产井附近影响最大。
(3)裂缝渗透率对页岩气产能具有较大影响:裂缝渗透率越大,日产气量越大,稳产期越短;裂缝渗透率越小,日产气量越小,稳产期越长;裂缝渗透率越大,页岩累积产气量越大,裂缝渗透率小于5× 10-3μm2时,不同裂缝渗透率下累积产量的差别较大。当裂缝渗透率大于5×10-3μm2时,裂缝渗透率对累积产量的影响变小,生产后期累积产量已相差不大。
[1] U S Energy Information Administration.World shale gas resources:an initial assessment of 14 regions outside the United States[M].Washington:U S Department of Energy,2011.
[2] 张金川,金之钧,袁明生.页岩气成藏机理和分布[J].天然气工业,2004,24(7):15-18.
ZHANG Jin-chuan,JIN Zhi-jun,YUAN Ming-sheng. Reservoiring mechanism of shale gas and its distribution [J].Natural Gas Industry,2004,24(7):15-18.
[3] 陈尚斌,朱炎铭,王红岩,等.中国页岩气研究现状与发展趋势[J].石油学报,2010,31(4):689-694.
CHEN Shang-bin,ZHU Yan-ming,WANG Hong-yan,et al.Status and trends of shale gas in China[J].Acta Petrolei Sinica,2010,31(4):689-694.
[4] JAVADPOUR F,FISHER D,UNSWORTH M.Nanoscale gas flow in shale sediments[J].Journal of Canadian Petroleum Technology,2007,46(10):55-61.
[5] ROBERT G L,ROBERT M R,STEPHEN C R,et al. Morphology,genesis,and distribution of nanometer-scale pores in siliceous mudstones of the mississippian barnett shale[J].Journal of Sedimentary Research,2009,79: 848-861.
[6] REED R M,LOUCKS R G.Imaging nanoscale pores in the Mississippian Barnett shale of the northern fort worth basin[J].AAPG Annual Convention Abstracts,2007,6: 115.
[7] BIRD R B,STEWART W E,LIGHTFOOT E N.Transport phenomena[M].New York:John Wiley&Sons, 2002.
[8] OZKAN E,RAGHAVAN R.Modeling of fluid transfer from shale matrix to fracture network[R].SPE 134830, 2009.
[9] BUSTIN A M M,BUSTIN R M,CUI X.Importance of fabric on the production of gas shale[R].SPE 114167, 2008.
[10] MORIDIS G J,BLASINGAME T A,FREEMAN C M. Analysis of mechanisms of flow in tight-gas and shale-gas reservoirs[R].SPE 139250,2010.
[11] FREEMAN C M.A numerical study of microscale flow behavior in tight gas and shale gas reservoir systems [R].SPE 141125,2010.
[12] KAST W,HOHENTHANNER C R.Mass transfer within the gas-phase of porous media[J].International Journal of Heat and Mass Transfer,2000,43(5):807-823.
[13] FLORENCE F A,RUSHING J A,NEWSHAM K E,et al.Improved permeability prediction relations for lowpermeability sands[R].SPE 107954,2007.
[14] CUSSLER E L.Diffusion:mass transfer in fluid systems [M].New York:Cambridge University Press,2009.
[15] CIVAN F,RAI S C,SONDERGELD H C.Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms [J].Transport in Porous Media,2010,86(3):925-944.
[16] CLIFFORD K H,STEPHEN W W.Gas transport in porous media[M].The Netherlands:Springer,2006.
[17] KAZEMI H,MERRILL L S,PORTERFIELD K L,et al.Numerical simulation of water-oil flow in naturally fractured reservoirs[R].SPE 5719,1976.
[18] PEACEMAN D W.Interpretation of well-block pressures in numerical reservoir simulation with nonsquare grid blocks and anisotorpic permeability[J].SPEJ,1983,23 (3):531-543.
[19] 李亚军,姚军,黄朝琴,等.考虑渗透率张量的非均质油藏有限元数值模拟方法[J].计算物理,2010,27 (5):692-698.
LI Ya-jun,YAO Jun,HUANG Zhao-qin,et al.Finite element simulation of heterogeneous reservoir with full permeability tensor[J].Chinese Journal of Computational Physics,2010,27(5):692-698.
[20] 姚军,樊冬艳,王晨晨,等.考虑二次梯度项低渗透油藏水平井压力动态分析[J].石油学报,2011,32(3): 479-483.
YAO Jun,FAN Dong-yan,WANG Chen-chen,et al. Dynamic pressure analysis of horizontal wells in low permeability reservoirs with the effect of quadratic gradient term[J].Acta Petrolei Sinica,2011,32(3):479-483.
[21] 秦积舜,李爱芬.油层物理学[M].东营:中国石油大学出版社,2006.
(编辑 李志芬)
Transport mechanisms and numerical simulation of shale gas reservoirs
YAO Jun,SUN Hai,FAN Dong-yan,HUANG Zhao-qin,SUN Zhi-xue,ZHAGN Guo-hao
(School of Petroleum Engineering in China University of Petroleum,Qingdao 266580,China)
Based on dual porosity continuum media,the kinematic equations in matrix and fracture were built by using dusty gas model(DGM).Viscous flow,Knudsen diffusion,free molecular diffusion and gas adsorption-desorption in pore surface were considered in matrix,the Langmuir isotherm adsorption equation was used in the dual porosity model.Viscous flow, Knudsen diffusion and free molecular diffusion were considered in fractures.Matrix-fracture dual porosity numerical model was established and calculated by finite element method.The influence factors of shale gas production were analyzed based on the numerical simulation results.The results show that the produced gas comes from both free gas and desorbed gas.The influence of free gas on shale gas production is greater than that of desorbed gas,but the adsorption should be considered in prediction of shale gas production because the predicted shale gas rate is low without considering adsorption.The Knudsen diffusion and Klinkenberg effect have great impact on matrix apparent permeability especially near the production wells,and the matrix apparent permeability increases with production time prolonging.The shale gas production increases with the fracture permeability increasing,and the matrix permeability has little influence on shale gas production.
reservoir;shale gas;dual porosity media;dusty gas model(DGM);adsorption;finite element method;transport mechanism;numerical simulation
TE 312
A
1673-5005(2013)01-0091-08
10.3969/j.issn.1673-5005.2013.01.015
2012-09-24
国家自然科学基金项目(51234007);教育部博士点基金项目(20110133120012);中国石油大学(华东)自主创新项目(11CX05007A);国土资源部海洋油气资源与环境地质重点实验室开放基金项目(MRE201207)
姚军(1964-),男,教授,博士,博士生导师,主要从事油气田开发工程的教学和科研工作。E-mail:youcang@upc.edu.cn。
