关于童氏乙型水驱特征经验公式的探讨

郑 可,徐怀民,陈建文

(1.中国石油大学地球科学学院,北京 102249；2.中国石油大学油气资源与探测国家重点实验室,北京 102249； 3.中国石油长庆油田分公司超低渗透油藏研究中心,西安 710021)

关于童氏乙型水驱特征经验公式的探讨

郑 可1,2,徐怀民1,2,陈建文3

(1.中国石油大学地球科学学院,北京 102249；2.中国石油大学油气资源与探测国家重点实验室,北京 102249； 3.中国石油长庆油田分公司超低渗透油藏研究中心,西安 710021)

对目前广泛运用的童宪章水驱经验公式进行推导,在此基础上研究水驱特征曲线在矿场应用中存在的问题,对该经验公式进行修正,并提出计算水驱地质储量的新方法。根据中国3个油田共7个油藏的实际生产数据资料对提出的方法进行验证。结果表明:利用童宪章水驱经验公式预测的油藏最终采收率结果偏大,计算的水驱地质储量结果有误；利用修正后的方法计算的水驱地质储量更接近于用容积法计算的地质储量。

油藏；水驱特征曲线；含水饱和度；含水率；最终采收率；地质储量

童宪章等[1-2]提出的水驱油藏特征曲线及经验公式不但可以预测水驱油藏的可采储量和最终采收率等重要指标,而且还可以研究累积产水量、累积产油量、水油比、含水率以及含水上升率和采出程度等之间的相互关系,实用价值很高,成为一种重要的油藏工程方法[3-5]。但在长期的油藏开发实践中发现,童氏水驱特征曲线也存在问题,预测的油藏最终采收率和水驱地质储量一般偏大[6-8]。笔者对这些开发指标偏大的原因进行探讨,提出宜于矿场实际运用的修正方法并进行实例分析。

1 童宪章水驱特征经验公式推导

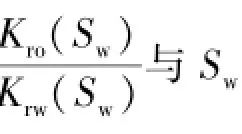
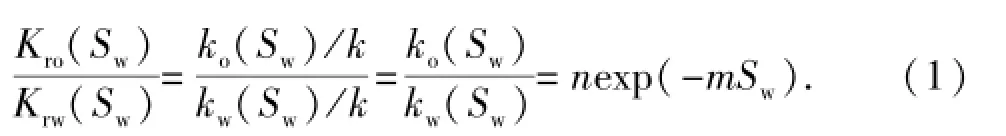
式中,ko(Sw)和kw(Sw)分别为油相和水相有效渗透率,10-3μm2；k为绝对渗透率,10-3μm2；m为直线的斜率；n为直线的截距。

m和n由岩石和流体的性质决定,岩石的渗透率、孔隙分布、流体黏度、界面张力和润湿性等不同, m和n也有所不同。

图1中Sm为含水饱和度最大值；S′为直线段末端对应的含水饱和度。

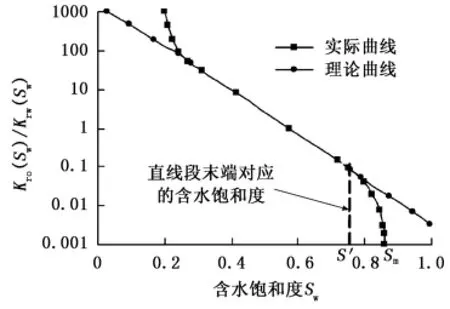
图1 油水相对渗透率比与含水饱和度关系Fig.1 Relation between ratio of oil-water relativepermeability and water saturation

根据油水两相渗流达西定律,油水两相体积水油比F[11]为

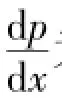
将式(1)代入式(2)得

由含水率定义并联立式(3)可得

式中,fw(Sw)为含水率；Qw和Qo分别为年产水量和年产油量,t；ρw和ρo分别为水和原油的密度,kg/ m3。

对式(4)两边求导得

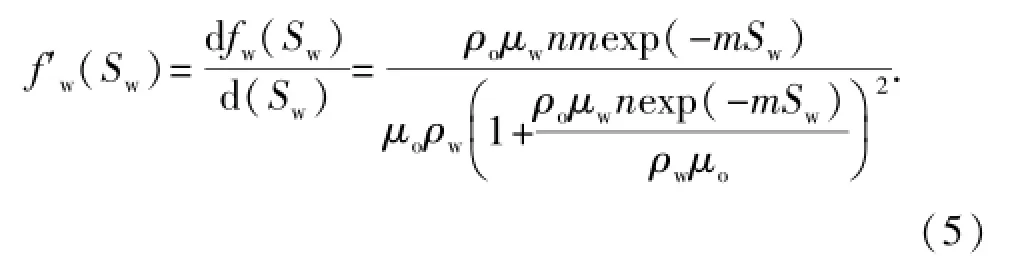
联立式(4)和式(5)得

如图2所示,根据Buckley-Leverett的线性驱替理论计算非活塞式水驱油模型[12-14],油水前缘出口端的平均含水饱和度与出口端含水饱和度Sw的关系为

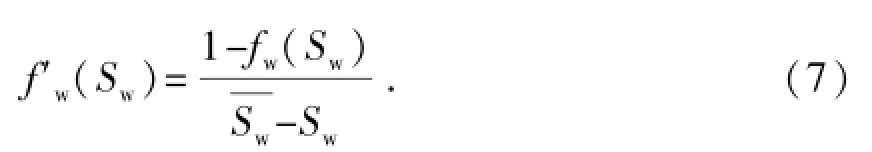
式中,f′w(Sw)为图2中C点的切线的斜率。

图2 水驱前缘出口端含水饱和度的确定Fig.2 Determination of outlet water saturation of waterflood front

油藏任一时刻的采出程度R[15]可表示为

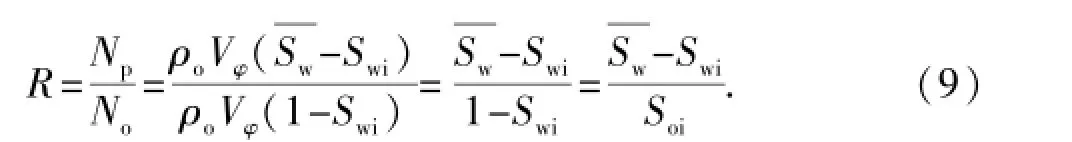
式中,Vφ为油藏孔隙总体积,m3；Np为任一时刻的累积采油量,t；No为地质储量,t；Swi为油藏束缚水饱和度；Soi为油藏原始含油饱和度。

将式(8)代入式(9)得

依据式(10)并联立式(6)求得的含水饱和度Sw为

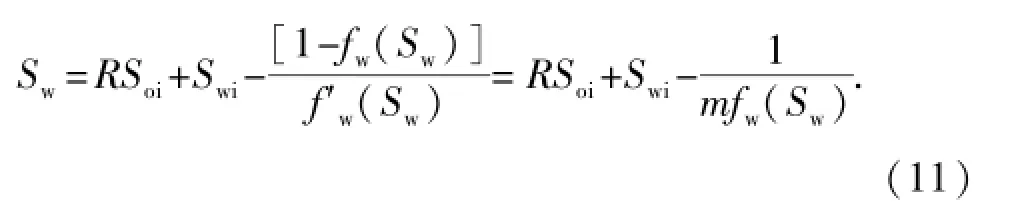
将式(11)代入式(3)得

引进矿场实际中常用的质量水油比(Rwo)并联立式(2)得

将式(12)代入式(13)得

当质量水油比Rwo相当大时,C=0,式(19)可简化为

式(20)即为童宪章提出的乙型水驱特征曲线关系式,从该式可以看出,在实际质量水油比Rwo值比较小时,Rwo与累积产油量Np在半对数坐标轴上并不呈直线关系,当油田生产一段时间后,在Rwo值比较大时,Rwo与Np在半对数坐标轴上才呈直线关系,以此来研究含水率与采出程度的关系,如图3是根据大庆油田南二区葡Ⅰ组矿场生产数据所绘制的Rwo和Np的关系曲线,具有典型乙型水驱特征曲线的特征。

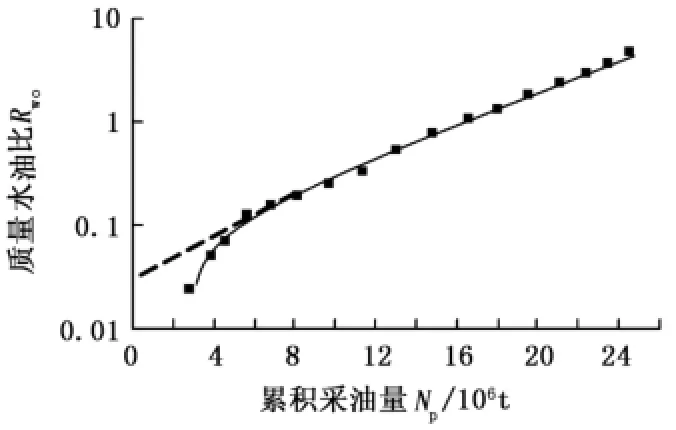
图3 大庆油田葡Ⅰ开发区乙型水驱特征曲线Fig.3 B-type water drive characteristic curve of PuⅠdevelopment area,Daqing Oilfield

2 矿场应用及存在问题

水驱特征曲线广泛运用于矿场实际生产中,这类曲线虽然是经验公式,但都有理论依据,因此能较准确地反映水驱油藏的开发指标变化规律。

值得注意的是中国各油田通常都用No=7.5B来计算水驱地质储量,系数7.5是童宪章[16]根据国内外25个油藏的大量资料统计而来的,从统计的角度看,这个值是很有价值的。

当No=7.5B时,由式(20)可得

联立式(4)、(13)得

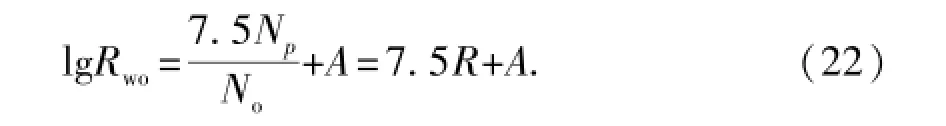
将式(23)代入式(22)可得

可以设想,对于一个实际的水驱油藏而言,当油藏的含水率达到0.98时,质量水油比Rwo值为49,此时的采出程度R可以看作最终采收率Rm,代入式(24)可得

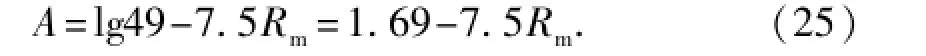
将式(25)代入式(24)可得

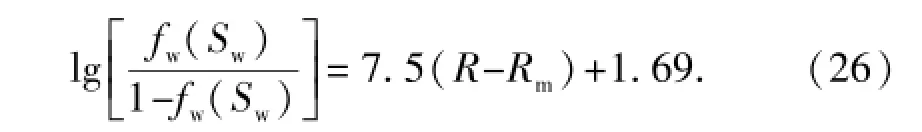
依据式(26),当Rm及R取不同的值时计算含水率fw(Sw)的值,得到水驱油藏含水率fw(Sw)和采出程度R的理论图版[17],图4即为童氏水驱特征曲线(油藏采出程度和含水率关系)理论图版。

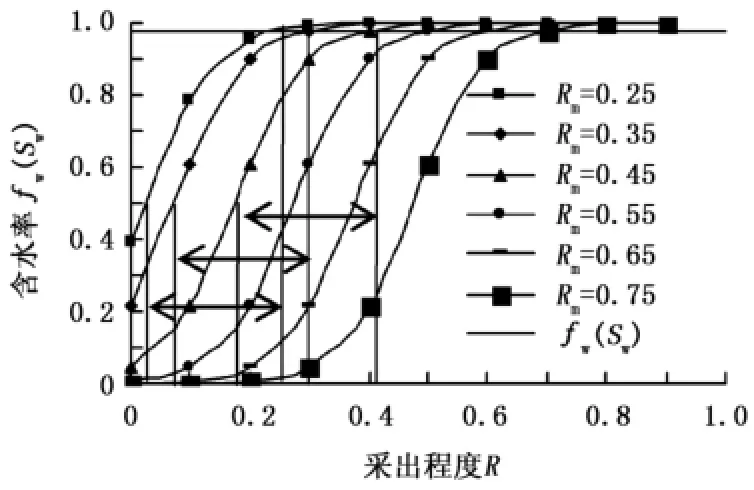
图4 童氏水驱特征曲线的采出程度与含水率关系图版Fig.4 Relation between recovery degree and water cut of Tongıs water drive characteristics curves

2.1 预测最终采收率的不合理性

当Rwo趋于无穷大(Rwo→∞)时,由式(17)得含水率等于1,分析式(20)能得出任一时刻的累积采油量Np趋于无穷大(Np→∞),这一结论显然不合理[18-20]。首先,因为式(20)是由式(1)推导而来的,当含水饱和度Sw=Sm时,由式(1)可以得出Kro(Sw)/Krw(Sw)＞0,说明当含水饱和度达到最大值时,仍然有油产出；只有当Sw趋于无穷大(Sw→∞)时,Kro(Sw)/Krw(Sw)=0,说明地层中有无穷多的油可以被驱替出来,即为任一时刻的累积采油量Np趋于无穷大(Np→∞),这是因为由式(1)表示的理论曲线在首尾端歪曲了实际曲线(图1),实际曲线不会有这样的不合理结论,从图1的实际曲线可以看出,当Sw=Sm时实际曲线斜率m趋于无穷大(m→∞),此时Kro(Sw)/Krw(Sw)=0,即Np为一个有限值。

由上述分析,根据式(17)、(20)可知,含水率为1时,累积产油量Np趋于无穷大(Np→∞),即采出程度趋于无穷大(R→∞)。在矿场实际运用中,以此来预测的油藏最终采收率(通常以含水率达到0.98时的采出程度为最终采收率)有偏大的可能。如何鉴别预测的最终采收率是否偏大很有必要。

在不考虑水驱地质储量准确性的情况下,可以利用式(11)来进行估算和判断,若式(11)计算的Sw小于图1中的S′值,则预测的最终采收率不会偏大,反之,则会偏大。现以长庆油田塞5区长2油藏为例,计算参数可根据该油藏的实际生产数据求得,其中参数R为预测的最终采收率Rm,可由式(24)线性回归和式(25)联立计算求得,为0. 5；Soi和Swi可根据归一化后的相渗曲线求得,分别为0.79和0. 21；m可由式(1)线性回归求得,为16. 35；fw(Sw)为0. 98；S′可根据图1线性回归计算求得,为0.55。将这些参数代入式(11)得Sw=0.5426＜S′=0.55,故长2油藏在含水率达到0.98时,所预测的最终采收率(Rm=0.5)不会偏大。

2.2 预测水驱地质储量的不合理性

尽管用No=7.5B来计算水驱地质储量从统计的角度看具有一定的价值,但具体到各个性质不同的油藏,会得出不合理的结论。

研究水驱曲线理论图版(图4),可得出以下结论:当最终采收率Rm分别为0.25、0.35、0.45时,含水率由0.5上升到0.98后采出程度变化似乎都是一个定值。即任何水驱油藏含水率由0.5上升到0.98后的阶段采出程度的变化值是一个确定的常数,这显然是不合理的。

由式(24)求得采出程度R,可得

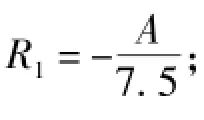
以上分析认为用No=7.5B来计算水驱地质储量不合理。如果仍然利用式(21)来计算水驱地质储量就不会存在这样的不合理结论。由式(21)求得B值:

将式(28)代入式(20)并简化,求得采出程度R的表达式为

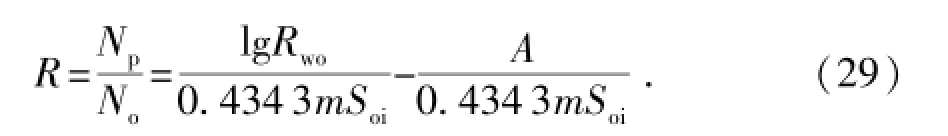
以上利用理论推导的方法对No=7.5B计算的水驱地质储量进行了分析,并说明了用No= 0.434 3mBSoi这种方法计算的水驱地质储量的合理性。以下运用新方法来计算长庆油田(延长组)2个油藏、大港油田(明化镇组、馆陶组、沙河街组)3个复杂断块油藏及大庆油田(葡一组)2个油藏的水驱地质储量,并对其进行比较,计算参数及计算结果见表1,其中B值可根据实际生产数据由式(20)线性回归求得。

表1的计算结果表明,用No=0.4343mBSoi比用No=7.5B估算的水驱地质储量更接近于用容积法计算的地质储量。

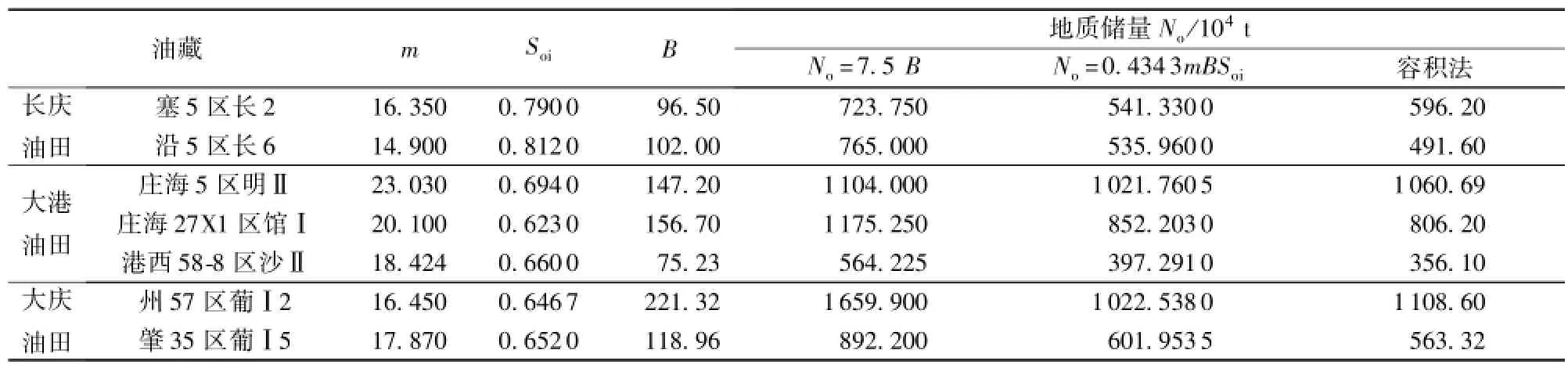
表1 两种不同方法计算水驱地质储量的比较Table 1 Comparison of water drive geological reserves calculated by two different methods

3 结束语

对目前矿场广泛应用的童宪章乙型水驱特征曲线进行了推导,对利用此类特征曲线预测的油藏最终采收率进行了不合理性分析,提出了鉴别最终采收率是否偏大的方法。分析了用No=7.5B来计算水驱地质储量时得到不合理的结论,即任何不同性质的水驱油藏,只要水驱特征曲线出现直线段后,在各相同含水阶段内,每采出1%的地质储量其含水率上升都相同。提出了用No=0.434 3mBSoi计算水驱地质储量的新方法。利用3个油田共7个油藏的实际生产数据进行验证,表明利用新方法计算的水驱地质储量更接近于用容积法计算的地质储量。

[1] 俞启泰,靳红伟.关于广义水驱特征曲线[J].石油学报,1995,16(1):61-69.

YU Qi-tai,JIN Hong-wei.Generalized water displacement curve[J].Acta Petrolei Sinica,1995,16(1):61-69.

[2] 童宪章.油井产状和油藏动态分析[M].北京:石油工业出版社,1981:37-60.

[3] 俞启泰.俞启泰油田开发论文集[C].北京:石油工业出版社,1999:29-37.

[4] 童宪章.应用童氏水驱曲线分析方法解决国内外一些油田动态分析问题[J].新疆石油地质,1989,10(3): 41-49.

TONG Xian-zhang.Application of Tongıs water drive performance curve analysis method to analysis some reservoir performance problems in the world[J].Xinjiang Petroleum Geology,1989,10(3):41-49.

[5] 林志芳,俞启泰,李文兴.水驱特征曲线计算可采储量方法[J].石油勘探与开发,1990,17(6):64-71.

LIN Zhi-fang,YU Qi-tai,LI Wen-xing.A method for estimating recoverable reserves of an oilfield by using the displacement characteristic curves[J].Petroleum Exploration and Development,1990,17(6):64-71.

[6] 凡哲元,任玉林,姜瑞忠.对童氏“7.5B”计算及乙型水驱法的改进[J].西南石油学院学报,2006,28(3):17-19.

FAN Zhe-yuan,REN Yu-lin,JIANG Rui-zhong.A new understanding to"7.5B"in MR.Tongıs formula[J]. Journal of Southwest Petroleum Institute,2006,28(3): 17-19.

[7] 林志芳,俞启泰,赵明.水驱特征曲线应用中的问题研究[J].石油勘探与开发,1986(5):37-44.

LIN Zhi-fang,YU Qi-tai,ZHAO Ming.A study on the application of water drive characteristics curves[J].Petroleum Exploration and Development,1986(5):37-44.

[8] 赵永胜,张四平,黄伏生.校正水驱曲线方法的改进及实例[J].石油勘探与开发,1993,20(3):49-53.

ZHAOYong-sheng,ZHANGSi-ping,HUANGFusheng.Improvement of the method of rectifying water drive characteristics curves[J].Petroleum Exploration and Development,1993,20(3):49-53.

[9] 杨胜来,魏俊之.油层物理学[M].北京:石油工业出版社,2004:260-267.

[10] IRAJ E,OSAZUWA O.A method for extrapolation of cut vs recovery curves[J].Journal of Petroleum Technology,1978,30(2):203-204.

[11] 葛家理.现代油藏渗流力学原理[M].北京:石油工业出版社,2003:175-212.

[12] BUCKLEY S E,EVERET M C.Mechanism of fluid displacements in sands[J].AIME,1942,146:107-116.

[13] HANS P L,ASLAK T,RAGNAR W.Instability of buckley-leverett flow in a heterogeneous medium[J]. Transport in Porous Media,1992,9:165-185.

[14] 张建国,雷光伦,张艳玉.油气层渗流力学[M].东营:中国石油大学出版社,2006:148-156.

[15] 陈元千.油气藏工程实践[M].北京:石油工业出版社,2005:357-368.

[16] 童宪章.天然水驱和人工注水油藏的统计规律探讨[J].石油勘探与开发,1978(6):38-79.

TONG Xian-zhang.Study on statistical regularity of water flooded and artificial water flooded oil reservoirs[J]. Petroleum Exploration and Development,1978(6):38-79.

[17] 姜汉桥,姚军,姜瑞忠.油藏工程原理与方法[M].东营:中国石油大学出版社,2006:236-245.

[18] CRAFT B C,HAWKINS M F.Applied petroleum reservoir engineering[M].New Jersey:Prentice Hall Inc, 1991:362-364.

[19] 喻高明.油藏工程[M].北京:石油工业出版社,2012: 174-175.

[20] WILLIAM D,MCAIN JR.Petroleum fluids[M].Oklahoma:Pennwell Publishing Company,1990:280-292.

(编辑 李志芬)

Study on Tongıs B-type water drive characteristics empirical formula

ZHENG Ke1,2,XU Huai-min1,2,CHEN Jian-wen3

(1.School of Geosciences in China University of Petroleum,Beijing102249,China；
2.State Key Laboratory of Petroleum Resources and Prospecting in China University of Petroleum,Beijing 102249,China；
3.Research Center of Ultra-low Permeability Reservoir,Changqing Oilfield Company,PetroChina,Xiıan 710021,China)

The water drive empirical formula proposed by TONG Xian-zhang was derived firstly,which is widely used currently.The problems in the field application of water drive curves were studied.A new method for calculating water drive geological reserves was developed.Actual production data of seven reservoirs in three oilfields were used to verify the new method.The results show that the reservoir ultimate recovery predicted by TONG Xian-zhang water drive empirical formula is on the high side,and the calculated water drive geological reserves have error.The water drive geological reserves calculated by the revised method are close to that calculated by volumetric method.

reservoir；water drive curve；water saturation；water cut；ultimate oil recovery efficiency；geological reserves

TE 341

A

1673-5005(2013)01-0099-05

10.3969/j.issn.1673-5005.2013.01.016

2012-05-09

国家科技重大专项(2011Z05009-003)

郑可(1984-),男,博士研究生,主要从事油气田开发地质及油藏研究。E-mail:zhengkelw@126.com。