交通监控中基于压缩感知的WMSN视频编解码
2013-07-05王世昌褚红亮杨成武
罗 晖,王世昌,褚红亮,杨成武
(华东交通大学信息工程学院,江西南昌,330013)
目前,在交通监控中,为实现对交通路况的实时视频监控,需要布置复杂的通信网络,以保证交通监控网络[1]长期稳定、可靠地运行。而无线多媒体传感器网络(wireless multimedia sensor networks,WMSN)[2]具备部署快速、组网灵活、感知信息丰富等优点。将WMSN用于交通监控中,不但可以实时获取路况场景的视频信息,而且能适应复杂多变的地理环境,其基本网络体系结构如图1所示。在监控区域内,视频传感器节点负责采集路况视频信息;簇头节点冗余部署在视频传感器节点周围,负责处理视频信息,并通过自组网以多跳中继方式将视频信息传输给汇聚节点;汇聚节点以无线通信方式将视频信息发送给交通远程监控中心。

图1 交通视频监控WMSN网络体系结构Fig.1 WMSN network architecture of traffic video surveillance
在上述交通视频监控WMSN网络中,视频信息数据量巨大,而WMSN传感器节点的能量、处理能力和存储资源受限。因此,研究一种高效的视频压缩编码方法就成为了WMSN应用于交通视频监控的关键。
近年来,由Candes和Donoho等人提出的压缩感知(compressed sensing,CS)[3]理论在信号采集和处理领域引起了国内外学者的广泛关注。CS理论指出,将一个稀疏或可压缩的高维信号投影到低维空间上,获取原始信号的观测值;同时,借助少量的观测值,可以通过一定的线性或非线性优化算法重构出原始信号。在CS处理过程中,因为观测值的个数远远少于Nyquist采样数,所以,如果将CS理论引入到视频图像编码中[4-6],就有望实现更有效的数据压缩和更准确的数据重构。这为视频编解码提供了一种新思路,也为WMSN应用于交通实时监控提供了可能。
2 压缩感知理论
假设一维有限长离散信号x∈RN×1,将其表示为N×1的列向量,所选取变换域空间的基函数为:,则x在Ψ 域表示为

式(3)是一个l0范数的优化问题,即NP-难问题,在多项式时间内难以求解,甚至无法验证其解的可靠性。理论分析表明,在一定条件下,l1最小范数和l0最小范数具有等价性,可以得到相同的解。那么将式(3)l0最小范数转换为l1最小范数

式中:α是x在Ψ上的表示系数,若它有K个分量不为零,而N-K个分量为零或者非常接近于零,就称x在Ψ域是K稀疏的或是近似K稀疏,也就是说,x是可压缩的。
在稀疏条件下,用一个M×N的观测矩阵Φ作用于信号x,获取的观测向量为y,则y=Φx,将式(1)代入,得到压缩感知数学表达式[7]

式中,Θ是CS算子,在数学上表现为一M×N矩阵,由于M≪N,因此,式(2)是个病态方程。但当Θ满足有限等距性质(restricted isometry property,RIP)[8]时,等价于Ψ 和Φ不相关,通过数学优化方法能够获得精确解[9]。因此,重构原始信号等价于求解一个优化问题,其优化目标表示如下

式(4)是一个非线性优化问题,可用贪婪追踪算法解此优化问题,如正交匹配追踪(OMP)算法[10],也可以将非凸问题转化为凸问题寻找信号的逼近,如基追踪(BP)算法[11]、快速迭代收缩阈值(FIST)算法[12]等。
3 基于CS的WMSN视频编解码
3.1 视频编码
在交通视频监控中,监测区域场景一般是固定的,连续视频帧图像的背景相同,且视频图像存在帧内帧间相关性。基于此特点,将视频图像组(group of picture,GOP)中的图像帧定义为关键帧和非关键帧再分别进行编码。
在编码过程中,将WMSN节点采集的每个GOP的第一帧作为视频图像关键帧,标记为I帧,其余的视频图像帧称作非关键帧,标记为Pj帧。同时,因一个GOP中的视频图像背景相似,帧间存在强相关性,借助I帧的图像信息,并利用帧间差值技术,可以获得Pj帧的残差帧视频图像ΔPj。
3.1.1 稀疏表示
对于交通视频图像,因其内容中车辆等目标图像的像素存在邻域相关,且细节丰富。而Symlets小波具有双正交、近似对称和紧支撑等特点,其小波系数在保持稀疏性时,能有效刻画图像细节信息。因此,可以选取Symlets小波对交通视频图像的I帧和残差帧视频图像ΔPj进行稀疏表示。

3.1.2 观测过程
在CS理论中,对信号进行重构,要求CS算子满足RIP特性,即观测矩阵与稀疏基函数相关性非常小。已有理论证明:随机高斯测量矩阵与绝大多数稀疏基不相关,且存储简单,因此,选用随机高斯测量矩阵作为观测矩阵对小波稀疏系数进行观测,可以最终获得重构视频图像所需要的采样信号。
1)I帧观测过程。设高斯测量矩阵是,其元素相互独立并服从0均值、方差为的高斯分布即

经过观测过程,获取的采样观测值为

对二维图像的观测是按列进行的,观测矩阵的行数,决定了视频图像采样值的多少。设计合适的观测矩阵,可以获得最优的观测值以重构出高质量的视频图像。
2)Pj帧观测过程。稀疏表示已获得了Pj帧的残差帧视频图像ΔPj,ΔPj与Pj相比较,ΔPj中的像素值更加稀疏,因此,经小波变换后,非零的小波系数非常少,为加快观测的实时性,由I帧观测矩阵构造出综合观测矩阵ΦP,对GOP中所有Pj帧的ΔPj进行综合观测,ΦP表示为

式中:Φ1=Φ2=…=Φj=Φ,Φj对应Pj帧的残差帧视频图像,残差帧视频图像ΔPj按式(5)进行处理后获得相应的小波系数,进而得到采样观测值为

由于非关键帧视频图像Pj经帧间差值技术处理和小波变换后,小波系数已经变得相当稀疏,且ΦP中的矩阵元素相同,因此,设计的综合观测矩阵降低了编码复杂性。
3.1.3 视频图像编码具体过程
基于以上分析,交通视频图像的编码过程如下:在每个GOP中,I帧经小波变换直接感知观测;对于Pj帧,先获取残差帧视频图像ΔPj,再经小波变换后,利用综合观测矩阵获取观测值,观测值经量化[13]和熵编码[14-15]后完成编码。具体如图2所示。
3.2 视频解码
在传统视频图像解码中,视频解码就是实现编码的逆过程。然而基于CS的交通监控WMSN视频解码中,重构视频是一个求解数值优化问题的过程。
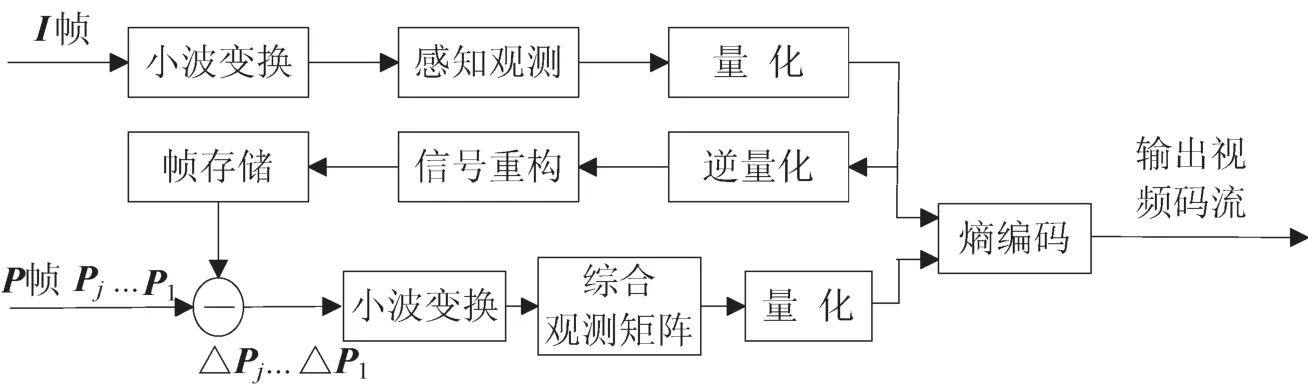
图2 基于CS的WMSN视频编码过程Fig.2 WMSN video encoding based on CS
3.2.1 解码算法
在解码端,CS重构过程中的优化目标函数为

利用拉格朗日算子将式(10)转化为无约束的优化问题

利用OMP算法迭代求解式(11),重构I帧和残差帧视频图像ΔPj,算法流程描述如下
输入:Θ=ΦΨ∈RM×N:CS采样算子矩阵
y∈RM×M:采样观测值
K:视频图像帧的稀疏度
中间变量:r∈RM×M:每次迭代产生的残差
Λt:t次迭代后,选出的所有算子向量索引λt的集合
初始化:r0=y,Λ0=φ,t=I

循环迭代K次,获得原始视频图像的近似表达
3.2.2 视频图像解码具体过程
在视频图像解码中,视频码流经过熵解码和逆量化后,获得了视频图像I帧和残差帧视频图像ΔPj的观测值。然后,在图像压缩感知重构中,通过运行OMP算法迭代处理相应的观测值,重构出GOP中的I帧图像和残差帧视频图像ΔPj,进而恢复出视频流。其解码具体过程如图3所示。

图3 基于CS的交通监控WMSN视频图像解码Fig.3 WMSN video decoding of traffic surveillance based on CS
4 实验仿真与分析
4.1 I帧视频图像编解码
在交通视频监控[15]中,Pj帧借助I帧信息完成重构,因此I帧的重构是视频重构的关键。在实验中,设置GOP中的原始I帧图像大小为256×256,通过改变观测次数重构图像,并对其进行比较,具体仿真结果如图4所示。图4(a)是未经处理的原始视频I帧图像;图4(b)是在观测次数为200时,重构出的I帧视频图像,该图中,在车辆聚集处,车辆之间的间隔不清,路标牌上的字迹模糊,这表明视频图像质量较差,其PSNR值仅为27.12 dB;图4(c)是在观测次数为300时,重构出的I帧视频图像,与图4(b)相比,其视觉效果更好,能辨出车间距离,字迹更清晰,没有明显的模糊效应,而且PSNR值达到32.94 dB。
因此,可以得出结论:在视频图像重构过程中,随着观测次数的增加,重构出的视频图像的质量更高、PSNR值也更大。

图4 实验仿真结果图Fig.4 The result pictures of experimental simulation
从视频图像质量的主观评价角度考虑,图像质量越高越好,那么需要相应地增大观测次数。但是,如果观测次数太大,就延长了重构时间,因此,需要依据交通视频监控标准设置合适的观测次数。
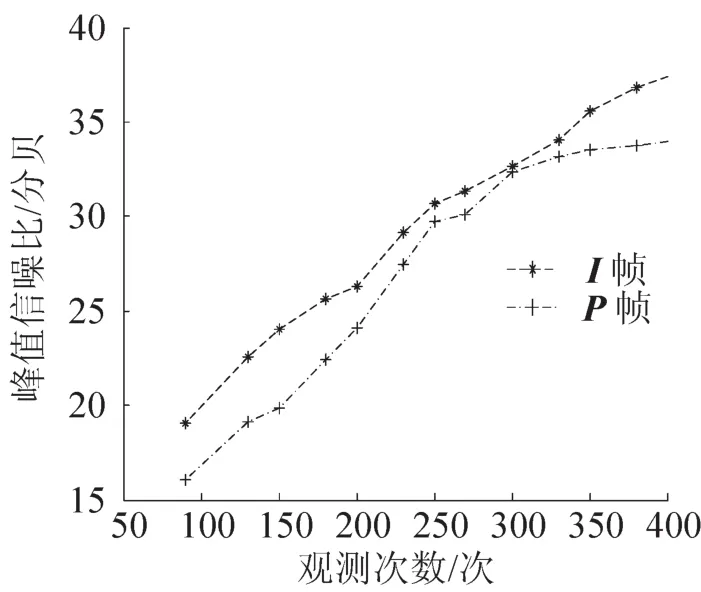
图5 实验仿真结果图Fig.5 The result pictures of experimental simulation
4.2 Pj帧视频图像编解码
对于Pj帧视频图像处理过程,采用与I帧相同的CS参数,当观测次数增加到一定程度时,重构出的Pj帧视频图像的PSNR值没有太大变化,结果如图5所示。在图5中,当观测次数大于300时,PSNR值基本不变。这种现象是因为:残差帧视频图像经Symlets小波变换后,小波系数已经相当稀疏,并且能重构出高质量的视频图像。因此,增加观测次数,重构出的Pj帧视频图像PSNR不会显著变化。
5 总结
在交通视频监控过程中,利用监控视频图像的帧内、帧间相关性,并采用压缩感知技术,对视频图像中的关键帧与非关键帧进行编解码。经实验仿真分析得出:该方法在恢复原始的视频图像过程中,不但大大减少了传输数据量,而且重构视频图像的PSNR值达到了30 dB以上。
[1]KUMAR P.Framework for real-time behavior interpretation from traffic video[J].IEEE Transaction on Intelligent Transportation Systems,2005,6(1):43-53.
[2]AKYILDIZ I F,MELODIA T,CHOWDHURY K R.Wireless multi-media sensor network:a survey[J].IEEE Transactions on Wireless Communication,2007,14(6):32-39.
[3]DONOHO D L.Compressed sensing[J].IEEE Transaction Information Theory,2006,52(4):1289-1306.
[4]WAKIN M B,LASKA J N,DUARTEM.F,et al.Compressive imaging for video representation and coding[C]//Processing Picture Coding Symposium,special session on Next Generation Video Representation,Beijing,2006:1-6.
[5]ROMBERG J.Imaging via compressive sampling[J],IEEE Signal Processing Magazine,2008,25(2):14-20.
[6]DUARTE M,DAVENPORT M,TAKHAR D,et al.Single-pixel imaging via compressive sampling[J],IEEE Signal Processing Magazine,2008,25(2):83-91.
[7]石光明,刘丹华,高大化,刘哲,林杰,王良君.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.
[8]TONG ZHONG.Sparse recovery with orthogonal matching pursuit under RIP[J].IEEE Transaction,2011,57(9):6215-6221.
[9]CANDES E J,WAKIN M B.An introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.
[10]TROPP J A,GIBERT A C.Signal recovery from random measurements via orthogonal matching Pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.
[11]CHEN S B,DONOHO D L,SAUNDERS M A,Atomic decomposition by basis pursuit[J].Siam Journal on Scientific Computing,1998,20(1):33-61.
[12]A.BECK,M.TEBOULLE.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].Siam Journal on Imaging Sciences,2009,2(1):183-202.
[13]Y.BAIG,E.M.K.LAI,J.P.LEWIS.Quantization effects on compressed sensing video[C]//17th International Conference on Telecommunications.IEEE,2010:443-446.
[14]THOMAS WIEGAND,GARY J SULLIVAN,AJAY LUTHRA,et al.Overview of the H.264 video coding standard[J].IEEE Transactions on Circuits and Systems for Video Technology,2003,13(7):1-19.
[15]郭厚焜,吴峰,黄萍.基于压缩感知和字典学习的背景差分法[J].华东交通大学学报,2012,29(1):43-47.
