θ型奇异积分算子在加权Morrey空间中的有界性
2013-07-05叶晓峰王腾飞胡媛媛
叶晓峰,王腾飞,胡媛媛,王 蒙
(华东交通大学基础科学学院,江西南昌330013)
算子在加权Lebesgue空间Lp(w)有界问题可以追溯到1972年Muckenhoupt在1972年文[1]中对Har⁃dy-Littlewood极大算子的讨论。文中提出了Ap权的概念,由此顺利解决了极大算子的加权有界性,并且使得加权理论如今成为调和分析的主要分支之一。2009年,Komori和Shirai在文[2]中首次提出了加权Mor⁃rey空间的概念,他们在文中讨论了极大算子以及Calderón-Zygmund奇异积分算子、分数次积分算子及其交换子在加权Morrey空间中的有界性。最近出现了很多这方面的结果,具体参见文献[3-8]。另外加权Morrey空间在偏微分方程中的应用,也得到了相应的推广,详见参考文献[9]。
奇异积分算子尤其是Calderón-Zygmund奇异积分算子在各种函数空间中的有界性的讨论是当代调和分析研究的主要问题。1952年,Calderón和Zygmund将这一算子推广到了Rn上,他们运用实变方法解决了算子在Lebesgue空间Lp(Rn)的有界性问题从而使调和分析在高维空间中有了新的发展。1985年,Yabuta在文[10]中首次提出了θ型奇异积分算子,并得到了Lp有界性, 1<p<∞。最近文[11]讨论了θ型奇异积分算子Lipschitz有界性的一个等价条件。另一方面,Hytönen在文[12]得到了θ型Calderón-Zygmund奇异积分算子在加权Lebesgue空间中的L2(w)有界性,并指出其最优上界为C(n,T,2)[w]A2。
2 定理及其证明
首先,我们来介绍加权Morrey空间的定义
定义1设1<p<∞,0<κ<1,w是权函数,对于Rn中的局部可积函数f(x)若满足,则称f(x)属于加权Morrey空间,并记其范数为
注意到当κ=0时,Lp,0(w)=Lp(w)是对经典的加权Lebesgue空间的推广。下面给出Ap权的如下定义
定义2设1<p<∞,若存在常数C≥1使得对于任意的正方体Q有
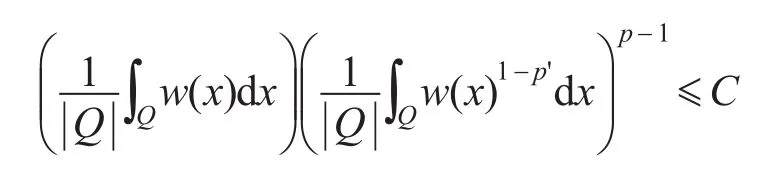
为了介绍θ型Calderón-Zygmund奇异积分算子,先给出连续模的定义。
定义3设θ(0)=0,称θ:[0,∞)→[0,∞)是一个连续模,若θ是次可加的,即θ(t+u)≤θ(t)+θ(u),并且单调递增。
从而可以定义θ型Calderón-Zygmund奇异积分算子为
定义4设θ(t)满足Dini条件,T是带有核K(x,y)且L2(Rn)有界的线性算子,满足:
2)对于任意的 ||x-y>2 ||x-x'>0有
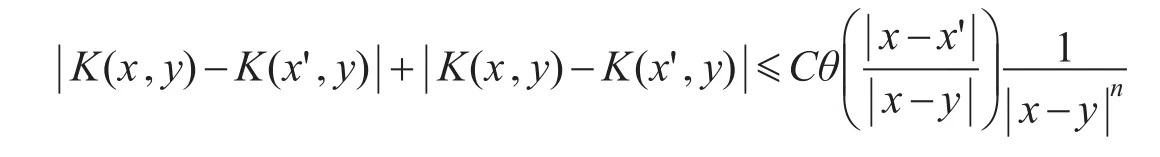
则K称为θ型Calderón-Zygmund核,称为θ型Calderón-Zygmund奇异积分算子。
因此,得到本文主要定理:
定理1设1<p<∞,w∈Ap,θ是连续模,并且T是θ型Calderón-Zygmund奇异积分算子,则T是Lp,κ(w)→Lp,κ(w)有界的。
为了证明该定理,需要如下引理。
引理1设w∈A2,函数θ是连续模,T是带有核K(x,y)的θ型Calderón-Zygmund奇异积分算子,则有

根据上面的结果,我们就可以通过外推法得到T的Lp(w)有界性,因此有必要介绍这一重要的定理,其证明可参考文献[13-14]。
引理2设T是次线性算子,满足存在p0:1<p0<∞使得对于任意的w∈Ap0有,则对任意的p:1<p<∞以及w∈Ap有
3 定理的证明
证明在方体3Q上考虑算子T的分解
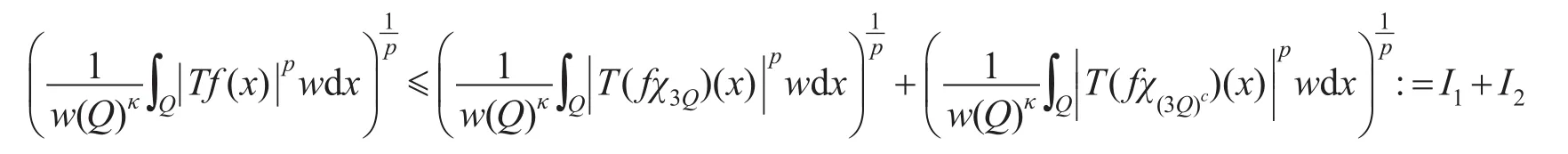
其中:χ3Q和χ(3Q)c为特征函数。
由引理1和引理2有
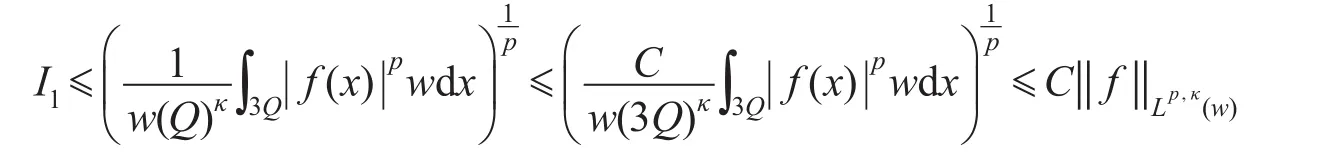
至于I2,取Rn中的范数为:,设Q的边长为l,x0为Q的中心,由几何关系知,对于任意的x∈Q以及y∈(3Q)c有。估计

对于任意的p>1,取p0使得1<p0<p。由于存在,且,使得
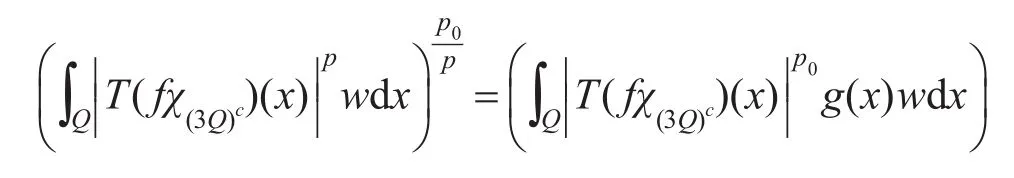
从而由Hölder不等式、Ap权定义有

结合前面I1的部分,从而有
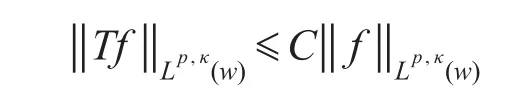
因此结论成立。
[1]MUCKENHOUPT B.Weighted norm inequalities for the Hardy maximal function[J].Trans.of the Amer Math Soc ,1972,165:207-226.
[2]KOMORI Y,SHIRAI S.Weighted Morrey spaces and a singular integral operator[J].Math Nachr,2009,282(2):219-231.
[3]YE X F.Some estimates for multilinear commutators on the weighted Morrey spaces[J].Mathematical Sciences,2012,6(33),6-11.
[4]王华,刘和平.Bochner-Riesz算子在加权Morrey空间上的一些估计[J].数学学报,2012,55(3):551-560.
[5]WANG H.The boundedness of some operators with rough kernel on the weighted Morrey spaces[EB/OL].(2010-11-26)[2013-01-07].http://arxiv.org/pdf/1011.5763.
[6]WANG H.Some estimates for commutators of fractional integrals associated to operators with Gaussian kernel bounds on weighted Morrey spaces[EB/OL].(2012-08-15)[2013-01-07].http://arxiv.org/abs/1202.5740.
[7]WANG H.Boundedness of fractional integral operators with rough kernels on weighted Morrey spaces[EB/OL].(2012-03-07)[2013-01-07].http://arxiv.org/pdf/1203.1441.
[8]WANG H.Intrinsic square function on the weighted Morrey spaces[J].Journal of Mathematical Analysis and Applications.2012,396(1):302-314.
[9]FU Z,LU S Z,SHI S G.Boundedness of sublinear operators on weighted Morrey spaces and applications[EB/OL].(2012-08-03)[2013-01-07].http://arxiv.org/pdf/1208.4788.
[10]YABUTAK.Generaization of Calderón-Zygmund operator[J].Studia Math,1985,82:17-31.
[11]陈跃辉,叶晓峰,刁俊东.一类带θ(t)型核的奇异积分算子的有界性[J].华东交通大学学报,2010,27(5):81-84.
[12]HYTÖNEN T.TheA2Theorem with the Dini condition[EB/OL].(2012-12-16)[2013-01-07].http://arxiv.org/abs/1212.3842.
[13]GARCÍAC J.An extrapolation theorem in the theory ofApweights[J].ProcAmer Math Soc,1983,87(3):422-426.
[14]周民强.调和分析讲义[M].北京:北京大学出版社1999:185-186.
