广义KdV-Burgers方程的势对称和不变解

朱永平,吉飞宇,陈晓艳

(1.西北大学数学系,陕西西安 710127;2.西安建筑科技大学理学院,陕西西安 710055)

广义KdV-Burgers方程的势对称和不变解

朱永平1,吉飞宇2,陈晓艳1

(1.西北大学数学系,陕西西安 710127;2.西安建筑科技大学理学院,陕西西安 710055)

用微分形式的吴方法讨论了广义KdV-Burgers方程不同系数情况下的势对称,并且利用这些对称求得了相应的不变解,这些解对进一步研究广义KdV-Burgers方程所描述的物理现象具有重要意义.

KdV-Burgers方程;微分形式的吴方法;势对称;不变解

1 引言

偏微分方程的对称理论和方法[1]是以求解线性微分方程的变量分离法,Fourier级数法及积分变换等为其特例的普适性方法,在求精确解和对称约化方面具有广泛的应用[23].由于古典对称方法在构造微分方程的对称中存在一定的局限性,因此,1981年Perk和Schultz提出了超对称,1994年Zhdanow和Fokas以及Liu提出了广义条件对称等,这些均是对古典对称的推广.1989年,Bluman提出的势对称理论[4]是扩充方程(组)对称的简便有效方法.近期,有许多学者致力于某些重要的非线性偏微分方程的势对称及不变解的研究,得到了许多重要成果[5-7].

在物理学中是一类非常重要的非线性波动方程,可看作是Burgers方程及Kuramoro-Sivashinsky方程组合的一种简单耗散模型.该类方程的很多理论结果受到了广泛关注[911].本文采用微分形式的吴方法[12]作为辅助计算,对KdV-Burgers方程的势对称和不变解进行了研究,将方程中系数的各种情况分类讨论,获得了与以往文献不同的势对称和不变解,并且大大降低了求解确定方程组的难度.

2 广义KdV-Burgers方程的势对称和不变解

2.1 基本理论

假设给定方程的自变量是x,t,其中u=u(x,t)是未知函数,并且该方程可以写成守恒形式:

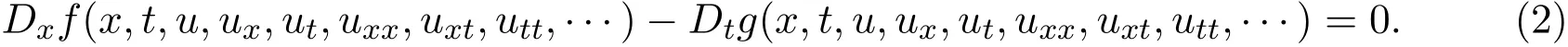
引入势变量v,得到方程(2)的辅助系统:

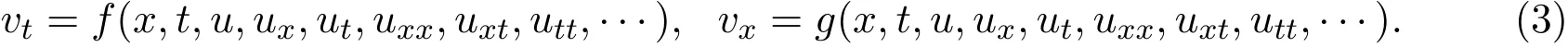
设辅助系统的(3)的古典对称向量为:

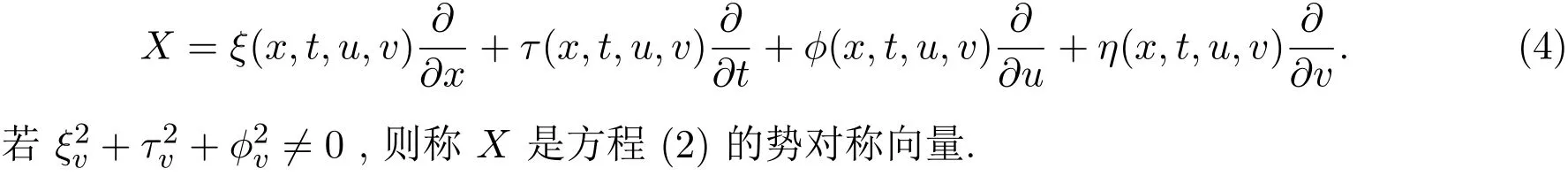
2.2 广义KdV-Burgers方程的势对称和不变解

将方程(1)写成守恒形式:

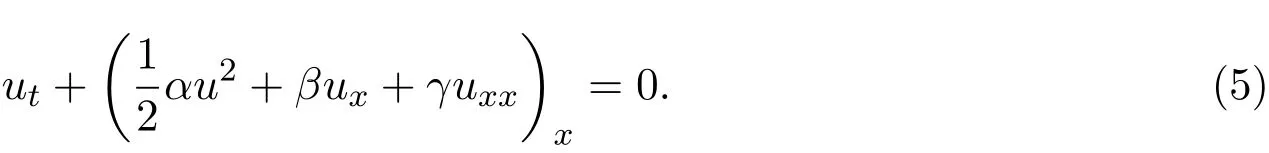
引入势变量v,得到相应的辅助系统:

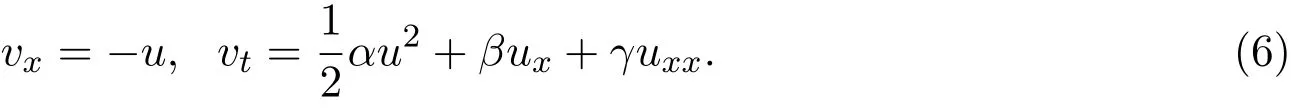
设方程组(6)对应的古典对称向量为:

下面对方程组(6)的系数α,β,γ分八种情形进行讨论.

情形1α/=0,β/=0,γ/=0.

用微分形式的吴方法计算得到(6)式的确定方程组为:

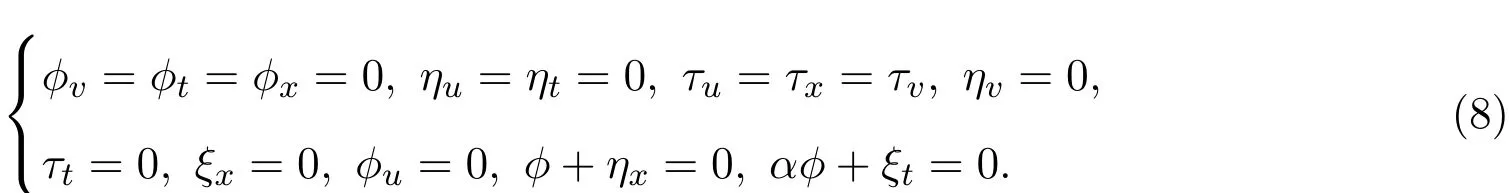
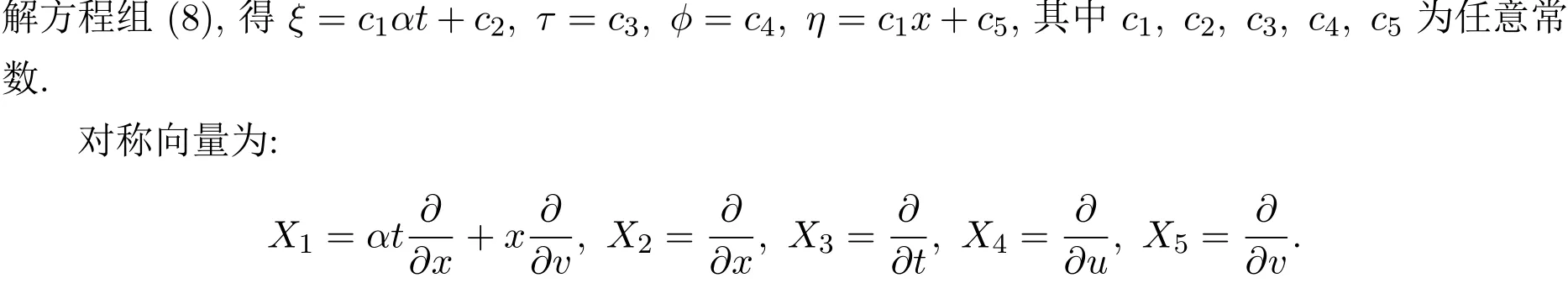
3 结论

本文利用微分形式的吴方法计算了广义KdV-Burgers方程在不同系数情况下的势对称,并且求得了对应的不变解,获得了与以往文献不同的结果.这对进一步研究广义KdVBurgers方程具有重要的意义.对于可写成守恒形式的微分方程在什么样的情况下允许势对称,有待于继续研究.

[1]Peter J Olver.Applications of Lie Groups to Differential Equations[M].New York:Spring-Verlag,1986.

[2]王珍,吉飞宇.mKdV方程的对称和群不变解[J].纯粹数学与应用数学,2011,27(6):778-780.

[3]姬利娜,张颖.多孔介质方程的广义条件对称和精确解[J].纯粹数学与应用数学,2011,27(3):339-342.

[4]George W Bluman,Sukeyuki Kumei.Symmetries and Integration Methods for Differential Equations[M]. New York:Spring-Verlag,1989.

[5]Gandarias M L.New potential symmetries for some evolution equations[J].Physica A,2008,387(10):2234-2242.

[6]张红霞,郑丽霞.Benney方程的势对称和不变解[J].动力与控制学报,2008,6(3):220-222.

[7]饶云高,朝鲁.广义KdV-Burgers方程新形势下的势对称分类[J].内蒙古工业大学学报,2012,31(1):1-6.

[8]郭柏灵.一类更广泛的Kdv方程的整体解[J].数学学报,1982,25(6):641-656.

[9]Ablowitz M J.Clarkson P A.Solitons,Nonlinear Evolution Equations and Inverse Scatting[M].New York: Cambridge University Press,1991.

[10]Zhang S L,Wang Y,Lou S Y.Approximate generalized conditional symmetries for perturbed evolution equations[J].Commu.Theor.Phys.,2007,47(6):975-980.

[11]Zhang S L,Li J N.Initial-value problem for extended KdV-Burgers equations via generalized conditional symmetries[J].Chinese Physics Letters,2007,24(6):1433-1436.

[12]朝鲁.微分方程(组)对称向量的吴-微分特征列算法及其应用[J].数学物理学报,1999,19(3):326-332.

Potential symmetries and invariant solutions of generalized KdV-Burgers equation

Zhu Yongping1,Ji feiyu2,Chen Xiaoyan1
(1.Department of Mathematics,Northewest University,Xi′an710127,China; 2.School of Science,Xi′an University of Architecture and Technology,Xi′an710055,China)

In this paper,the symmetries of generalized KdV-Burgers equation with different coefficients are discussed with the help of Wu′s method in differential forms.And new potential symmetries are obtained. Furthermore,the corresponding invariant solutions can be obtained by using the above symmetries.The solutions have are of great importance to further researching the physical phenomena described by generalized KdVBurgers equation.

KdV-Burgers equation,Wu′s method in differential forms,potential symmetries, invariant solutions

O175.2

A

1008-5513(2013)02-0164-08

10.3969/j.issn.1008-5513.2013.02.009

2012-11-22.

国家自然科学基金(10671156).

朱永平(1986-),硕士生,研究方向：偏微分方程.

2010 MSC:35Q53