局部对称流形中具有常平均曲率的完备超曲面

张剑锋,洪涛清

(丽水学院数学系,浙江丽水 323000)

局部对称流形中具有常平均曲率的完备超曲面

张剑锋,洪涛清

(丽水学院数学系,浙江丽水 323000)

讨论了局部对称黎曼流形中具有常平均曲率的完备超曲面的性质,通过Laplace算子的计算,得到一个关于第二基本形式模长平方S的拼挤定理,推广了已有的结果.

局部对称;超曲面;完备;全脐

1 引言

2 预备知识

设M是等距浸入局部对称流形Nn+1中的一个完备超曲面.在Nn+1上选择局部单位正交标架场{e1,…,en,en+1},使得限制在M时,e1,…,en与M相切,en+1是M的法向量.约定指标的变化范围如下:

其中等号成立当且仅当至少n-1个ai相等.

引理2.2[6,7]设M是Ricci曲率有下界的完备黎曼流形,F是M上有上界的C2-函数,则对任意ε＞0,存在一点x∈M,使得

3 定理的证明

当ε趋向于0时,由于F有界,不等式右边也趋向于0.选取点列{εm},使得εm→0(m→∞).则对应的存在点列{xm},使得点列{F(xm)}收敛(如果有必要,可以取子点列),不妨记收敛极限为F0.根据上确界的定义可知F0=supF,再根据F的定义可知

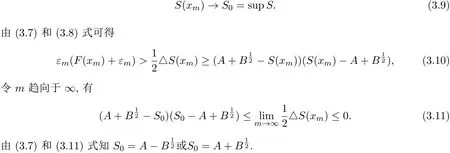
[1]Hlineva S,Belchev E.On the minimal hypersurfaces of a locally symmetric manifold[J].Locture Notes in Math.,1990,1841:1-4.

[2]水乃翔,吴国强.局部对称黎曼流形中的极小超曲面[J].数学年刊:A辑,1995,16(6):687-691.

[3]舒世昌,刘三阳.局部对称流形的具常平均曲率的完备超曲面[J].数学年刊:A辑,2004,25(1):103-108.

[4]张士诚,吴报强.局部对称黎曼流形中具有常中曲率完备超曲面[J].数学物理学报:A辑,2010,30(4):1000-1005.

[5]Okumura M.Hypersurfaces and a pinching problem on the second fundamental tensor[J].Amer.J.Math., 1974,96:207-213.

[6]Omor H.Isometric immersion of Riemannian manifolds[J].J.Math.Soc.Japan.,1967,19:205-214.

[7]Yau S T.Harmonic functions on Riemannian manifolds[J].Comm.Pure and Appl.Math.,1975,28:201-228.

[8]蔡开仁.欧氏空间中闭子流形的拓扑[J].数学年刊:A辑,1987,8(2):234-241.

Complete hypersurfaces with constant mean curvature in locally symmetric manifold

Zhang Jianfeng,Hong Taoqing
(Department of Mathematics,LishuiUniversity,Lishui323000,China)

In this paper,the complete hypersurfaces with constant mean curvature in locally symmetric manifold are investigated,a pinching theorem about the square of the length of the second fundamental form S is obtained by using the Laplace operator,which generalizes the known results.

locally symmetric,hypersurfaces,complete,totally umbilical

O186

A

1008-5513(2013)02-0118-07

10.3969/j.issn.1008-5513.2013.02.002

2012-11-12.

浙江省自然科学基金(Y6100218);丽水学院科研项目(KZ201113,KY201105).

张剑锋(1972-),博士,副教授,研究方向：微分几何.

2010 MSC:53B20,53A10