基于有限元法的斜齿轮齿廓修形技术研究

2013-07-03李恩仕汪中厚

制造业自动化 2013年10期

李恩仕，汪中厚

(上海理工大学机械工程学院，上海 200093)

0 引言

斜齿轮具有传动平稳、冲击、振动和噪声较小的优点[1]，在汽车、工程机械以及航空领域等得到了广泛的应用。但是由于实际的加工和装配中存在各种误差，以及材料本身的弹性变形等原因使得斜齿轮的性能受到了一定的限制[2～4]。齿廓修形是改善斜齿轮啮合特性，提高传动平稳性，降低齿轮传动噪声的重要手段之一。但是斜齿轮本身结构较复杂，采用传统的简化计算方法或经验公式难以精确的计算出斜齿轮真实的接触变形[5～7]，尤其是齿轮传动系统受载变形以后，容易造成轮齿接触不均匀，因此载荷分布情况比较复杂[8]。难以指导斜齿轮的精确齿廓修形。

随着有限元技术的不断发展，很多学者对基于有限元方法的齿廓修形技术做了大量的研究。张红丽通过对直齿轮进行有限元接触分析，反复计算齿轮旋转啮合的各个位置，得到了合理的齿廓修形经验值[9]。吴勇军等对斜齿轮单齿模型进行有限元啮合仿真分析，直接提取接触线上沿啮合线方向的综合弹性变形作为斜齿轮齿廓修形的修形量，取得了很好的修形效果[7]。尚振国等进一步研究了斜齿轮多齿对分析模型，根据有限元分析结果，通过公式转换计算出斜齿轮的齿廓修形量[10]。综上所述，斜齿轮的齿廓修形研究正在和快速发展的有限元方法结合起来。本文进一步建立了更为符合实际情况的全齿简化模型，同时通过对齿廓修形量进行二次修正的方法，考虑了修形后齿面变化和齿根圆角改变对齿廓修形量的影响。通过对修形前后齿轮模型的啮合性能、接触区域与接触性能的对比分析，全面的评价了斜齿轮的修形效果。

1 标准齿轮和修形齿轮建模

1.1 标准斜齿轮精确建模

精确的斜齿轮模型是有限元分析的基础，本文采用ProE软件进行斜齿轮建模。要在Pro/ E 中精确构建圆柱斜齿轮，必须引入齿形参数来控制轮齿形状，用关系工具建立原始参数、非独立参数以及轮齿结构尺寸之间的联系，利用曲线方程生成渐开线和螺旋线[11]。为了确保斜齿轮的精度，本文采用混合扫描切除材料的方法进行齿轮建模。采用混合扫描方法，旋转偏移草图数量大于5个时，模型精度会比较高[11]，本文采用9个旋转偏移草图来确保斜齿轮模型的高精度。

1.2 修形斜齿轮建模

修形齿轮具有和标准齿轮相同的螺旋线，并在渐开线齿廓未修形的部分发生重合，本文通过修改标准斜齿轮模型的草图的方法来建立修形斜齿轮的模型。草图修改方法为：引用标准斜齿轮建模的草图，根据计算得到的斜齿轮的修形参数，按照抛物线方程计算修形齿廓各处偏移距离（偏移距离的数值精确到1×10-5mm），通过二次曲线拟合得到修形齿轮的端面齿廓。

表1 斜齿轮基本几何参数

本文所要研究的变位斜齿轮的基本几何参数如表1所示，大小齿轮的材料如表2所示。

表2 齿轮材料特性

2 有限元模型建立

2.1 几何剖分和网格划分

根据分析要求可以在保留齿轮整体结构不变的基础上，将斜齿轮啮合传动中不参与啮合的轮齿进行简化，同时考虑到圣维南原理的作用，在参与接触的轮齿左右各保留一个不参与啮合的轮齿，保证精度的同时也方便结果的提取。

在有限元分析中，高质量的六面体网格不仅可以获得比四面体网格更高的精度也能更好的保证计算结果的正确性。为了划分出高质量的六面体网格，我们首先需要在AnsysWorkbench软件中对斜齿轮模型进行合理的剖分如图1所示。最终生成的六面体网格模型如图2所示。

图1 齿轮几何剖分

图2 最终网格模型

2.2 提取修形量时分析设置

在实际的齿轮工作中，大齿轮为主动齿轮，通过齿面之间的接触作用带动小齿轮旋转，大齿轮的输入扭矩为：137143N.mm。

在提取齿轮修形量的有限元计算时，按照本文3.1节中接触面设置方法进行。为了便于修形量的提取，设置小齿轮为主动轮。对小齿轮内孔施加Cylindrical类型约束，放开Tangential方向的位移约束。并对小齿轮内孔施加120000N.mm的扭矩。对大齿轮的内孔面施加Fixed Support约束，约束大齿轮内孔的全部自由度。

2.3 结果验证时的分析设置

在进行齿轮修形结果验证时，对参与接触的齿面全部设置接触。对大齿轮内孔施加Cylindrical类型约束，放开Tangential方向的位移约束。并对大齿轮内孔施加137143N.mm的扭矩。对小齿轮的内孔面施加Fixed Support约束，约束小齿轮内孔的全部自由度。这样，就构建了一个符合齿轮实际啮合情况的有限元模型。

3 修形参数计算

齿廓修形包括修形量的计算，修形长度的确定和修形曲线的选择。修形长度与修形曲线的研究都比较成熟，本文重点讨论修形量的计算。

3.1 齿顶修形量

在标准渐开线斜齿轮进入啮合时，如图3(a)所示，图中主动齿轮为大齿轮，被动齿轮为小齿轮。理想的没有弹性变形的齿轮副，主动齿轮在①处进入啮合瞬间，主被动齿轮恰好进入啮合状态。而实际工作齿轮啮合时，由于②、③处接触轮齿的齿面弹性变形，轮齿的弯曲、扭转变形等的综合影响，主动齿轮在进入啮合瞬间，被动齿轮的齿顶会和主动齿轮齿根部进入啮合的位置产生干涉从而导致啮入冲击的产生[12]。相对干涉量△1就是小齿轮的齿顶修形量。

在有限元求解计算时，我们考虑斜齿轮修形后的啮合状态。修形前①处的齿面由于弹性变形的影响会存在干涉量△1，而修形后①处的轮齿齿面刚刚进入啮合，①处齿面不受力。在有限元软件中对齿轮接触位置②③处设置面面接触，而对接触面①处按照自由状态进行处理。

有限元分析后，将位移结果转换到以小齿轮内孔为中心并以小齿轮轴线为旋转轴的圆柱坐标系下，提取图3(a)中小齿轮上的A点的位移值既为干涉量△1，如表3所示。

3.2 齿根部修形量

在标准渐开线斜齿轮退出啮合时，如图3(b)所示，由于接触面①②处齿轮齿面弹性变形，轮齿弯曲、扭转等变形的综合影响，导致大齿轮在啮出时主动齿轮的齿顶与被动齿轮的齿根产生干涉，从而导致被动齿轮齿面的刮伤。考虑到加工工艺性、减少修形工作量、降低修形成本等，通常只对小齿轮修形而大齿轮不修形[13,14]。图3(b)所示被动齿轮齿根部干涉量△2既为小齿轮齿根部的修形量。进行有限元接触设置时，图3(b)中①②处设置面面接触③处保持自由状态。

有限元分析后提取图3(b)中小齿轮上与大齿轮齿顶B相啮合的点绕小齿轮轴线旋转的位移值既为修形量△2如表3所示。

3.3 修形量二次修正

初步修形后小齿轮的齿面和齿根过渡圆角都会发生变化，这导致初步修形后得到的修形齿轮达不到理想的修形效果。对修形后的小齿轮按照3.1和3.2中相同的接触设置方法重新进行修形量的提取如表3所示。可见，二次修正后小齿轮的齿顶修形量和齿根部修形量都有所增加。最终确定出小齿轮的齿顶修形量为17.3μ m，齿根部修形量为15μ m。

图3 齿轮的啮合

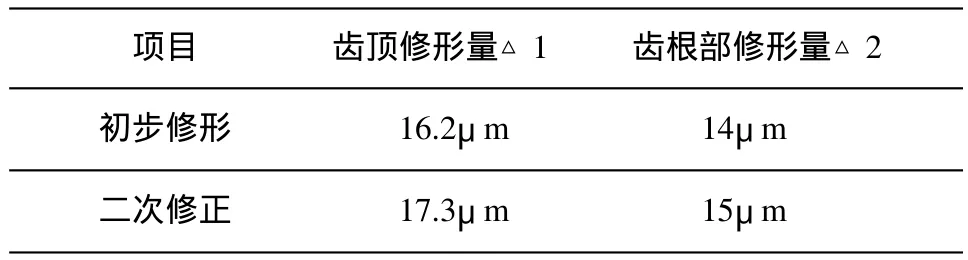
表3 修形量计算结果

3.4 修形长度与修形曲线

本文斜齿轮重合度为2.24，重合度较小，适合采用短修形方式进行修形，修形长度公式为：

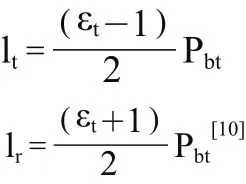
其中：lt为齿顶修形长度；lr为齿根部修形长度。

修形曲线选择抛物线形式，修形曲线方程为：

其中：inx为任意点x的修整量；jn为最大修形量。

4 收敛性验证与数据可靠性

4.1 接触假设与理论计算

由于斜齿轮接触的复杂性，为了精确的计算斜齿轮的齿面接触压力。如图4所示，我们以大齿轮端面齿廓分度圆处的曲率半径为半径建立一个各径向截面都与小齿轮各径向截面在小齿轮分度圆处啮合的螺旋圆柱体，螺旋圆柱体的宽度等于大齿轮宽度，螺旋圆柱体的半径R为：

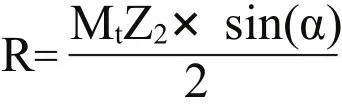
式中：mt为大齿轮端面模数；zz为大齿轮齿数；α为斜齿轮压力角。

根据接触力学与机械设计[16,17]可知，齿面接触应力计算公式为：

式中：F为作用于接触面上的总压力；B为初始接触线长度。

小齿轮分度圆上的圆周力Ft为[18]：

式中：T1为小齿轮扭矩；T1为小齿轮分度圆直径

垂直于接触面的法向力F为：

由于螺旋圆柱体与斜齿轮在各径向截面内都在分度圆处啮合，啮合线为一条轴向的直线，因此接触线长度为：B=14.5mm。

又知：μ1= μ2=0.3

E1=E2=205000

假设小齿轮扭矩为T1=60000N.mm。带入赫兹接触公式可得бH=735MPa

图4 螺旋圆柱体与小齿轮啮合

4.2 齿面接触力数据收敛与可靠性

按照2.2节的约束方式进行设置，并对小齿轮内孔施加60000N.mm的扭矩。通过不断细化网格，小齿轮齿面的最大接触应力值逐渐收敛于720MPa，与理论计算结果基本一致。证明了三维模型与边界条件的设置都是正确的。

图5 接触压力分析结果

5 齿轮修形及修形效果验证

5.1 齿面受力变化

齿轮轮齿主要受拉或者受压，因此我们考虑齿轮齿面的最大主应力的变化如图6所示。修形后的轮齿在啮入和啮出时刻齿面最大主应力都有明显的降低，这有利于改善齿轮的啮合性能，使齿轮在啮入与啮出时的过渡更加平稳。可见，本文的齿廓修形方法可以显著地改善斜齿轮的传动性能，减小啮入和啮出冲击。

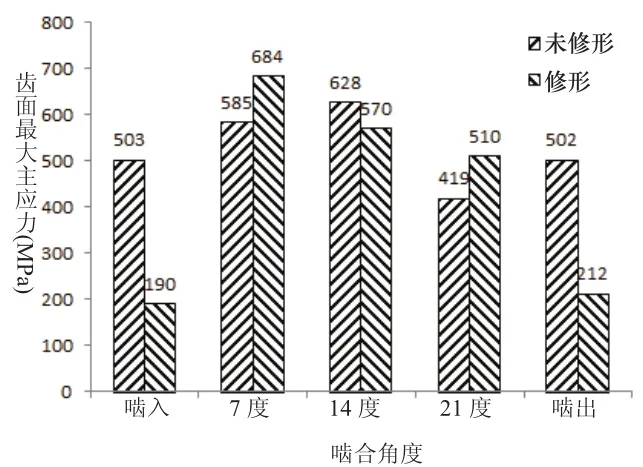
图6 齿面最大主应力变化

5.2 接触区域与接触应力分布

提取修形前后小齿轮在一个啮合周期内不同旋转角度下的齿面接触线，将各个角度下的接触线整理到一个齿面上得到修形前后小齿轮的接触区域的分布如图7和图8所示。修形前小齿轮的接触区域在齿高方向分布于从小齿轮的齿顶边界到小齿轮齿根部与大齿轮齿顶接触的边界。修形后小齿轮的接触区域往分度圆的方向收缩，小齿轮齿顶和大齿轮齿顶都不再参与啮合。

分别提取修形前后小齿轮齿面7°和21°接触线上的接触压力分布如图9和图10所示，修形前小齿轮齿面载荷分别在齿根部和齿顶处出现尖峰，最大接触应力分别为1390MPa和1630MPa，都出现了明显的边缘接触现象。修形后齿面载荷分布在齿根部和齿顶处的尖峰消失，接触线载荷分布平稳增大后又平稳的减小，齿面最大接触应力分别变为1251MPa和1210MPa，消除了小齿轮齿根部和齿顶处的边缘接触现象，改善了斜齿轮齿面的啮合性能。