频谱细化算法分析

赵宏强

(海军航空工程学院 青岛校区，山东 青岛 266041)

频谱分析是信号处理中最常用的方法，传统的频谱分析方法一般采用快速傅里叶变换(FFT)，FFT 得到的是整个折叠频率上的粗略的“全景频谱”，而在实际应用中，往往需要对感兴趣的窄带频谱区间进行细微观察和分析，这就需要较高的频率分辨率。FFT 算法中频率分辨率和采样点数成反比，在采样频率不变的前提下，要提高频率分辨率，就必须增加采样点数，但增加采样点数就会增加FFT 的计算量。因此，FFT 的频率分辨率和计算量是相互矛盾的，这也在一定程度上限制了FFT 的应用。

为了解决对窄带频谱区间进行细致观测的问题，提出了频谱细化的概念，其基本思路是对信号频谱中的某一频段进行局部放大，实现选带分析。频谱细化技术近年来发展迅速，常见算法有:FFT-FS 算法、ZOOM-FFT(以下简称ZFFT)算法和线性调频Z 变换(Chirp-Z 变换，以下简称CZT)算法。本文主要对上述三种频谱细化算法的原理进行比较，通过仿真分析总结各自的应用特点，并从频率分辨率的角度对三种算法的实质进行了分析研究。

1 频谱细化算法的原理

设采样序列为x(n)，n =0，1，…，N-1，采样频率为fs，需要进行细化的频带为f1～f2，对信号进行N 点FFT 变换。因此，

信号初始的频率分辨率为Δf=fs/N，选带的中心频率为f0=(f1+f2)/2，带宽为fW=f2-f1。

1.1 FFT-FS 频谱细化原理

序列x(n)的傅立叶系数:

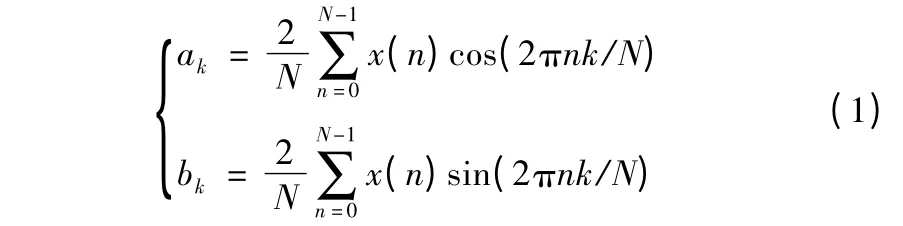
式(1)中，k=0，1，…，N/2。

频率kΔf 处幅值谱矢量表达式为ak-jbk，即ak和bk分别对应频谱幅值的实部和虚部。由采样定理知，序列x(n)中包含着0 ～fs/2 的频段信息，所以如果用连续的傅立叶变换对频谱进行计算，把频谱曲线看成是连续的，即把式(1)中的k 看作区间(0≤k≤N/2)内连续变化的实变量f(0≤f≤fs/2)，则可将式(1)变成:

于是，利用式(2)便可得连续的频谱曲线，从而使频率分辨率不再受采样点数N 的限制，f 是一个连续的频率。这便是FFT-FS 频谱细化算法的基本原理［1］。

在实际运用中，在定义域f∈［f1，f2］内，直接采用式(2)进行计算，然后根据所需的频率分辨率Δf '来设定选频带内的取样点数M，两者之间的关系为Δf ' =fW/(M-1)。

1.2 CZT 频谱细化原理

N 点FFT 计算的频谱实际上是z 平面单位圆上的N 点等间隔取样，CZT 计算的则是z 平面螺旋线周线上Z 变换的等间隔取样，这些取样在螺旋线的某一部分上按等角度分布。X(z)表示序列x(n)的Z 变换，利用CZT 算法，可以计算下列给定点zk上的X(zk)。

式(3)中A=A0e-jθ0，W=W0e-jφ0，A0和θ0分别表示起始抽样点z0的矢量半径长度和相角，W0表示螺旋线的伸展率，φ0表示两相邻抽样点之间的角度差，M 为所要分析复频谱的抽样点数，不一定等于N。按式(3)给定的zk值，经过推导，可得X(zk):

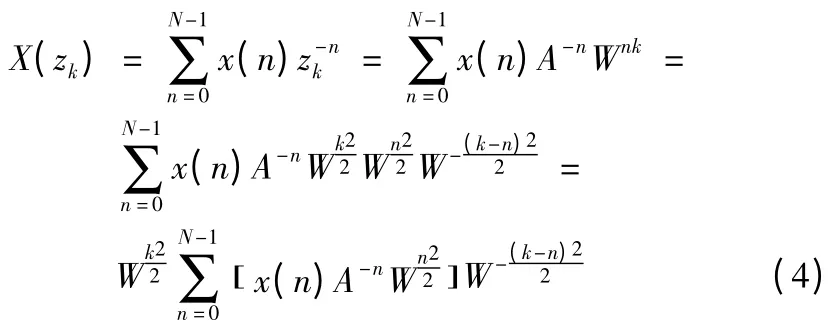
令

则

式(7)中，

以上便是CZT 频谱细化算法的基本原理［2-5］，其计算流程如图1 所示。

图1 CZT 的计算流程

在实际运用中，首先根据所需的频率分辨率Δf '来设定选频带内的取样点数M，两者之间的关系为Δ f ' =fW/(M-1)，然后根据选频带f1～f2确定CZT 的相关参数，因为希望得到的是信号的频谱分析，故应该在单位圆上去实现CZT，所以取A0=W0=1，θ0=2πf1/fs，φ0=2πΔf '/fs，最后根据图1的计算流程进行CZT 计算。

1.3 ZFFT 频谱细化原理

ZFFT 频谱细化算法的基本原理可归纳为［6-8］:将初始信号与单位复指数信号exp(-2πnf0/fs)相乘进行复调制，将实序列变为复序列，利用傅里叶变换的移频性质把选频段的中心频率移至零频，再通过低通抗混叠滤波和整数倍抽取，最后对抽取后的信号做FFT 分析和频率调整，便可以得到选频段的细化频谱。ZFFT 的计算流程如图2 所示。

在实际运用中，首先根据所需的频率分辨率Δf ＇来设定重采样的细化倍数D，两者之间的关系为Δf ' = fs/DN =Δf/D，假设要进行N 点FFT 变换，信号的长度为L，则D 的取值范围应满足DN≤L;然后根据选频带f1～f2确定低通滤波器的参数，滤波器的截止频率fd的取值范围应满足fd≤fs/2D;最后再根据图2 的计算流程进行计算即可。

图2 ZFFT 的计算流程

2 仿真算例分析

2.1 仿真算例1

设仿真信号为:x(t)=cos(2π×203t)+cos(2π ×203.9t+π/3)，信号的采样频率为1 024 Hz，采样点数为1 024 点，频率分辨率为Δf=1 Hz。分别采用基带FFT、ZFFT、FFT-FS和CZT 对信号进行分析，分析结果如图3 所示。

在由基带FFT 得到的全景频谱中，无法分辨出信号中的两个频率成分，通过局部放大FFT 频谱，尽管可以得到两个极大值，但由于两频率成分间隔为0.9 Hz ＜Δf，所以不能确定信号是单频信号还是多频信号。通过设定参数，对频带200 ～205 Hz 进行细化，使三种频谱细化算法的频率分辨率都为0.1 Hz，三种算法都能看到两个明显的峰值，可以确定信号是由两个频率构成的多频信号。从而验证了三种频谱细化算法的有效性。

图3 基带FFT、FFT-FS、CZT 和ZFFT 的分析对比

尽管FFT-FS 与CZT 频谱细化的算法不同，但是由图3可以看出两者的细化结果非常接近，为了进一步研究，分别对抽样点M 为11、21 和51，即频率分辨率分别为0.5 Hz、0.25 Hz 和0.1 Hz 三种情况下对上述仿真信号进行了分析，两者频谱幅值绝对误差的数量级都为10-13，如图4 所示。因此，FFT-FS 与CZT 的仿真结果可以认为是一致的，在下面的仿真中仅以FFT-FS 作为代表进行分析。

当多频信号中频率间隔较小时，两频率之间会产生干涉现象，上述仿真条件不变，FFT-FS 与ZFFT 的频率分辨率都为Δf ＇1=0.1 Hz，改变信号两频率的大小进行分析。当频率间隔为5Δf ＇1时，分析结果如图5(a)所示，FFT-FS 仍能分辨出两个频率，但发生了峰值漂移，有了相互排斥的现象，幅值衰减达20%;当频率间隔为2Δf ＇1时，分析结果如图5(b)所示，FFT-FS 已经不能分辨出两个频率，即使增加抽样点数M也无济于事，由于两频率的叠加使幅值增加30%;但是在这两种情况下，ZFFT 都能正确分辨出信号中的两个频率，并且频率和幅值估计值几乎没有误差。尽管两次仿真的频率间隔都大于FFT-FS 细化后的频率分辨率，但是FFT-FS 对于密集多频信号间的干涉无能为力，不能有效分辨密集多频信号，而ZFFT 却可以有效抑制信号间的干涉，高精度地分辨密集多频信号。

ZFFT 之所以有很高的分辨精度，并能抑制频率间的干涉，主要是因为进行ZFFT 仿真时，所需的数据长度是FFTFS 的D 倍(D 为细化倍数)，它的高分辨率是以增加数据长度来实现的。实际上，ZFFT 的性能与对原数据做DN 点FFT后，在选频带内的局部放大的效果相近。

以上的仿真都是在没有噪声干扰的情况下进行的，下面将在不同信噪比(SNR)下，对DN 点的FFT、ZFFT、FFT-FS 和CZT 4 种算法的性能及特点进行比较。

图4 FFT-FS 与CZT 频谱幅值的绝对误差

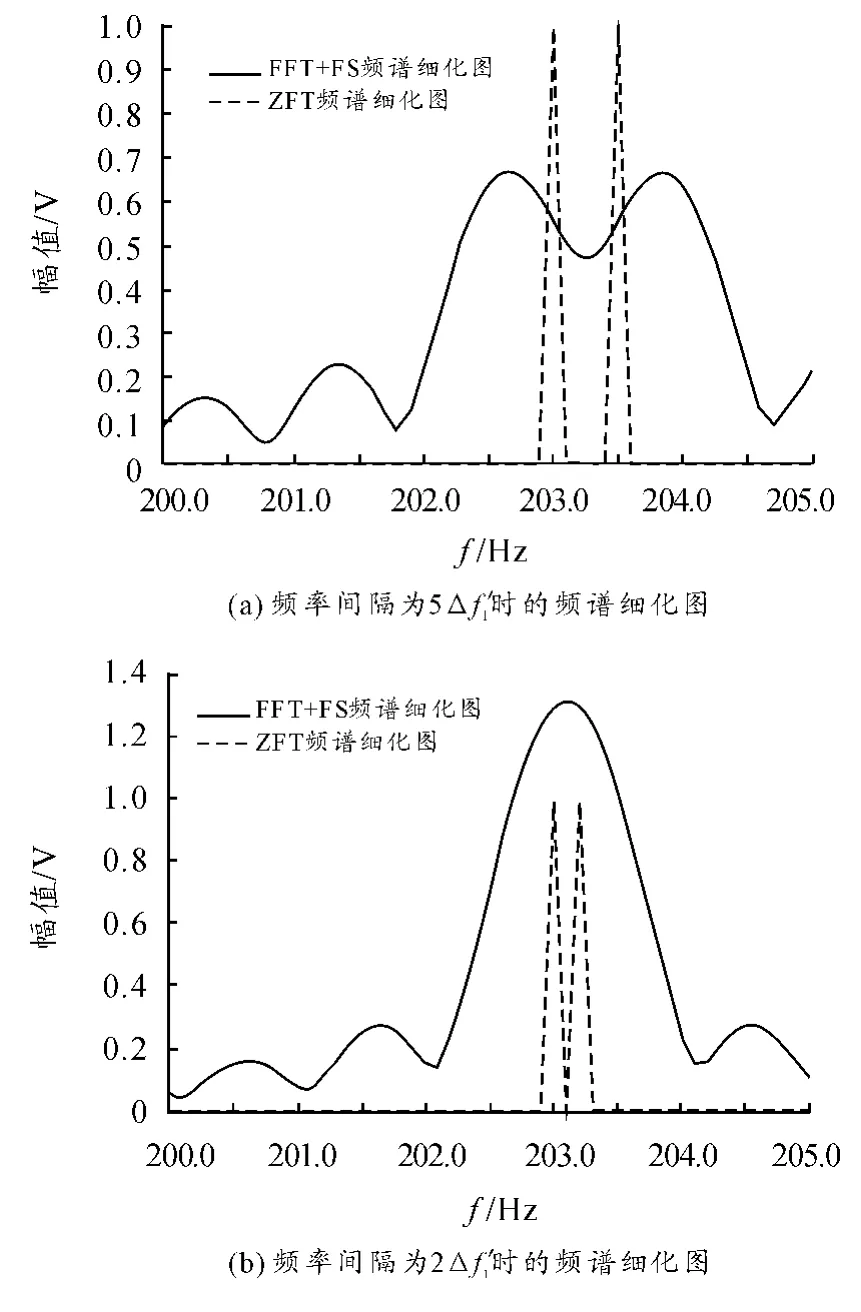
图5 FFT-FS 与ZFFT 的分析对比图

2.2 仿真算例2

设仿真信号:x1 = 2cos(2π × 203t + 10π/180)，x2 =cos(2π×203.85t+20π/180)，x3 =2cos(2π ×203.7t +10π/180)，x4 =cos(2π×203.83t+20π/180)

s(n)为加性高斯白噪声，信号的采样频率为1 024 Hz，采样点数为1 024 点，初始频率分辨率为1 Hz，令ZFFT 中的D=20，FFT-FS 和CZT 中的M=51，选频带为200 ～205 Hz，从而保证3 种算法细化后的频率分辨率都为Δf ＇2=0.05 Hz。算例(A-C)分别是在SNR =-10，0，10 三种情况下对信号x1 +x2 +s(n)进行的仿真，算例(D-F)是在SNR =10 的情况下分别对信号x2 +x3 +s(n)、x1 +x4 +s(n)、x4 +s(n)进行的仿真，所有的仿真结果都是在进行了1 000 次蒙特卡洛仿真后取的平均值，如表1 所示。

1)上述所有情况下的仿真都表明，DN 点的FFT 和ZFFT 的性能是接近的，FFT-FS 和CZT 的性能是接近的，一般情况下可认为彼此是一致的，下面仅以ZFFT 和FFT-FS 两种方法为代表进行比较;

2)由算例(A-C)可得，随着SNR 的增加，ZFFT 的性能得到提高，频率、幅值和相位三者的误差都变小;FFT-FS 只有相位误差变小，而频率和幅值误差变化不大;尽管随着SNR 的增加ZFFT 和FFT-FS 的性能都得到一定程度的改善，但改善程度较小，因此，两种方法的抗噪性都较好;

3)算例(F)是一个单频信号，而算例(E)比(F)多了一个频率接近的信号，但仿真结果显示FFT-FS 的幅值误差和相位误差在(F)中比在(E)都小了一个数量级，频率误差也小了一倍，性能得到明显提高;而ZFFT 性能变化不大。说明了FFT-FS 比较适合于单频信号的频谱细化，否则精度将受到影响;

4)算例(D)与(C)相比，只是缩小了两频率间的频率间隔，但FFT-FS 的频率、幅值和相位误差分别为10Δf ＇2，43.2893%和24.560 1 度，信号已经完全失真，而ZFFT 的性能却几乎没有受到任何影响。证明了FFT-FS 不适用于频率间隔较小的密集多频信号，而ZFFT 却可以有效抑制频率间的干涉;

5)算例(D)和(E)相比，只是其中一个信号的频率成分由203.85 Hz 改为了203.83 Hz，但仿真结果显示ZFFT 在(E)中的幅值误差达25%，相位误差近75 度，信号完全失真;算例(F)中对频率为203.83 Hz 的单频信号进行分析，ZFFT 在(F)中的误差和(E)接近，并没有得到改善。这主要是由于203.85 Hz 是整周期采样(Δf ＇2=0.05Hz)，而203.83 Hz 不是整周期采样。因此，ZFFT 仅适用于整周期采样的信号，其估计精度较高，对非整周期采样的信号分析其复制和相位就会完全失真，算例(F)也说明即使是对单频非整周期采样信号也无能为力。比较而言，FFT-FS 对于信号是否是整周期采样影响不大。

表1 各种频谱细化方法的性能比较

3 频谱细化算法的本质分析

频谱细化算法之所以能够对选频段的频谱进行细化，根本原因在于频率分辨率的提高，下面从频率分辨率的含义入手，对频谱细化算法的本质就行分析。

文献［3］对频率分辨率进行了较详细的阐述，给出了物理分辨率Δfp=fs/L 和计算分辨率Δfc=fs/N 两个概念，其中fs为采样频率，L 为信号长度，N 为FFT 的变换点数。计算分辨率是靠计算得出的，它并不能反映真实信号的频率分辨能力，而真正反映信号频率分辨能力的是物理分辨率，在采样频率不变的前提下，要提高信号的分辨能力，只能通过增加数据的实际长度来实现。

FFT-FS 和CZT 频谱细化算法本质上是相同的。就是在不增加数据长度的前提下，用不同的数学处理方式在选频带内通过插值，增加FFT 的变换点数，从而提高信号的计算分辨率，实现对局部频段的细化，但不能提高物理分辨率，因而不能改善信号的频率分辨能力。

ZFFT 频谱细化算法通过滤波重采样使采样频率fs降低D 倍，因而物理分辨率变为fs/DL，进而提高频率分辨能力，但该过程隐含的条件是对原始数据长度增加D 倍后进行的重采样，实际数据长度为DL，信号最初的物理分辨率也为fs/DL。因此，ZFFT 并不能提高信号的物理分辨率，它只是在假定信号长度为L 不变的错误前提下，通过一系列数学变换使得选频带内物理分辨率貌似从fs/L 提高到了fs/DL，得到了提高频率分辨能力的假象，而信号的物理分辨率在整个过程中并没有改变，通过ZFFT 得到的改善频率分辨能力的结果，并不是通过ZFFT 算法实现的，根本原因在于信号数据长度的增加。ZFFT 的实际效果和对信号直接进行DN 点FFT变换是一致的。综上可得，ZFFT 本质上并不能真正实现频谱细化，它只是一种节省运算量的快速算法。

4 结论

介绍了当前三种频谱细化算法的原理，通过大量的仿真对各种算法的特点进行研究，最后通过频率分辨率的概念对各种算法的本质进行了分析。

1)ZFFT 和DN 点FFT 变换是一致的，它并不能真正实现频谱细化，它只是一种节省运算量的快速算法。ZFFT 可以改善信号的频率分辨能力，但以增加数据长度为代价。ZFFT 对整周期采样信号进行分析，在SNR=-10 dB 的情况下，频率误差为0，幅值误差约为4%，相位误差小于3 度;但对于非整周期采样，即使在SNR=10 dB 的情况下，幅值误差达25%，相位误差近75 度。因此，ZFFT 仅适用于整周期采样的信号分析，精度较高。

2)FFT-FS 和CZT 在本质上是一致的，灵活性较好，可以对选频带进行任意倍数的细化，不受信号长度的影响，但不能改善信号的频率分辨能力，不适用于密集信号的分析。在SNR=10 dB 的情况下，当频率间隔为3Δfc 时，频率误差为10Δfc，幅值误差约为45%，相位误差大于20°。FFT-FS 对单频信号分析精度较高，对多频信号分析，频率和相位误差都较大，不如ZFFT 效果好。但FFT-FS 的估计精度不受信号是否为整周期采样的影响，适用范围更广。

［1］刘进明，应怀樵.FFT 谱连续细化分析的傅里叶变换法［J］.振动工程学报，1995，8（2）:162-166.

［2］程佩青.数字信号处理教程［M］.第2 版.北京:清华大学出版社，2001.

［3］胡广书. 数字信号处理-理论、算法与实现［M］. 第2版.北京:清华大学出版社，2003.

［4］RABINER L，SCHAFER R，RADER C.The chirp z transform algorithm［J］.IEEE Transactions on Audio and Electroacoustics，1969，17（2）:86-92.

［5］钱克矛，李川奇.频谱校正的线性调频Z 变换方法［J］.振动工程学报，2000，13（4）:628-632.

［6］丁康，潘成灏，李巍华.ZFFT 与Chirp-Z 变换细化选带的频谱分析对比［J］.振动与冲击，2006，25（6）:9-12.

［7］李天昀，葛临东. 两种快速频域细化分析方法的研究［J］. 系 统 工 程 与 电 子 技 术，2004，26（9）: 1192-1194，1216.

［8］王力，张冰，徐伟.基于MATLAB 复调制ZOOM-FFT 算法的分析和实现［J］. 舰船电子工程，2006，26（4）:119-121.

［9］丁明亮，罗久飞，郭小渝.单侧声带息肉的声学信号特征［J］. 重庆理工大学学报:自然科学版，2011（8）:60-65.