时温等效原理在车辙预估中的应用
2013-07-02徐忠乾
徐忠乾,李 昶
(东南大学 交通学院,江苏 南京 210096)
沥青路面车辙是目前高速公路的主要病害之一,车辙主要是在外因(气候、交通)及内因(材料性能、路面结构)共同影响下,轮迹带处的路面沥青材料产生的侧向剪切和蠕变变形累计而形成的永久变形[1-2]。车辙深度的预估对路面材料的性能控制具有指导意义。目前,有限法广泛应用于沥青路面车辙计算中,通过对沥青路面瞬态温度场的模拟,利用连续变温沥青路面车辙有限元法计算车辙深度[3]。
时温等效原理是指升高温度和延长作用时间对高聚物的粘弹行为是等效的,目前在非晶体结构材料中的应用已经很成熟[4]。沥青混合料作为粘弹性材料时间效应与温度效应的等效性也得到了论证和验证[5]。本文结合具体工程进行车辙深度的预估,利用时温等效原理将低温作用时间转化为高温作用时间,由传统的连续变温沥青路面车辙计算转变为恒温作用下的沥青路面车辙计算,提高车辙预估计算速度,得到预估车辙深度,并由现场观察资料验证预估方法的准确性。
1 工程背景及研究思路
1.1 工程介绍
南方城市某新建高速公路工程的结构形式为半刚性基层沥青路面,上面层为SMA-13,中面层为SUP-20,下面层为SUP-25,厚度分别为4,6,8 cm,水泥稳定碎石基层厚40 cm,石灰土底基层厚20 cm。该地区最热的2个月为7,8月,最低气温为27℃,最高气温度为35℃,高温季节代表性气温以及月平均气温如图1,2所示。经现场调查和测试发现,该地区半刚性基层沥青路面5 a车辙量深度为10~20 mm不等。该地区交通量的当量轴次为12 989次/d,24 h交通量变化曲线如表1所示,现在该工程需要进行5 a车辙深度的预估,用以对路面各层材料的抗车辙性指标提供依据。
1.2 研究思路
1)完善针对沥青混合料的时温等效方程,确定 Williams-Landell-Ferry(WLF)方程[5]中的系数C1和C2。
2)针对工程实际结构,建立有限元模型,分析路面结构温度场,得到不同季节一天24个时刻结构内部不同点位的温度数据,作为时温等效转化的依据。

图1 南方城市7月24 h代表性气温
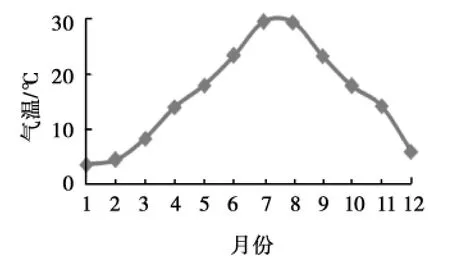
图2 南方城市月平均气温

表1 每小时内车辆通过率
3)车辆荷载按照方形均布的垂直作用形式简化,求出模型中的荷载作用时间,并根据交通量的分布情况,得到1 d不同时段的荷载作用时间。
4)根据步骤2)和3)中的温度和荷载时间数据,利用步骤1)中的时温等效方程,将不同季节较低温度下的作用时间转化成高温季节固定温度作用时间。
5)将步骤4)中高温作用时间输入已建立的有限元计算模型,该计算方法即为恒温作用下沥青路面车辙计算方法。
6)最后将计算结果与工程实际中的观测数据进行对比,验证时温等效原理在车辙预估中的适用性。
2 工程应用
粘弹性材料的力学行为对于温度和加载时间具有明确的依赖性,大量试验证明,沥青混合料在很宽广的温度范围内具有热流变简单材料的特性。对于简单热流变材料,可通过移位因子进行时温转换,通过高温短时间的作用得到低温下长时间的应力松弛特性,即温度变化对沥青混合料的影响可以通过时间尺度的折算来表征[5]。
由不同温度下应力松弛试验得到不同的松弛模量,在双对数坐标下绘制不同温度下松弛模量图,如图3所示。时温等效性可以理解为松弛函数的图像在以时间为横坐标的坐标体系统中(对数坐标)向左或向右平移一段距离,这个距离一般表示为估计温度t下的移位因子取对数后的值,如图4所示。
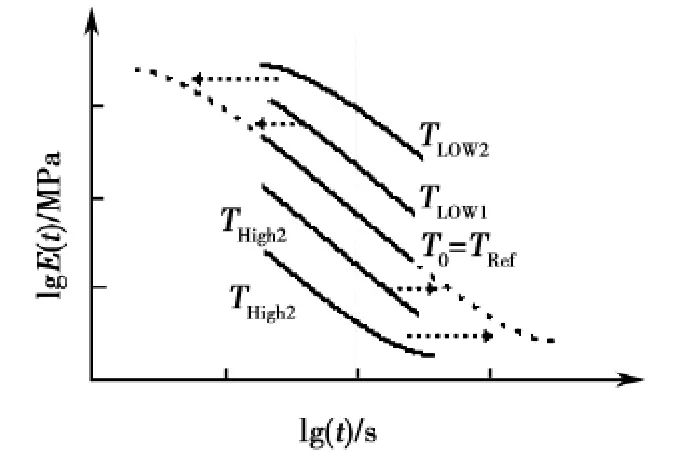
图3 不同温度下松弛模量平移示意图
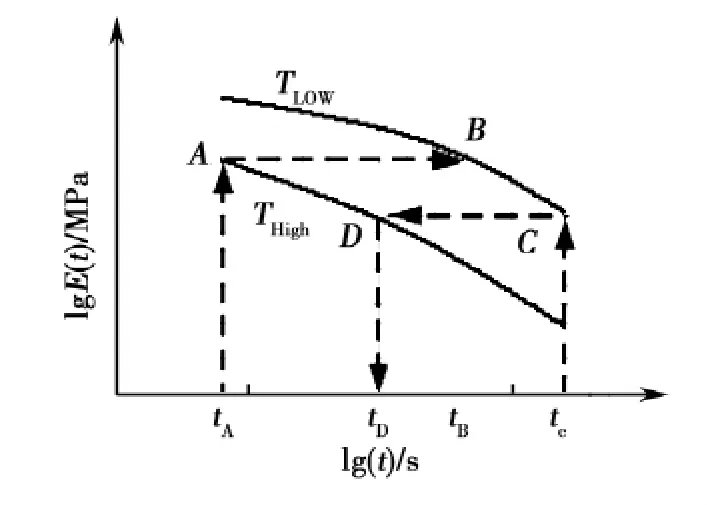
图4 不同温度移位示意图
采用半理论半经验公式WLF方程[5]计算经典的移位因子
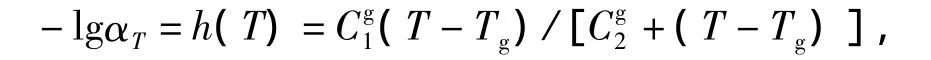
式中 lgαT为移位因子,lgαT=lgt0-lgt,其中t0为参考温度T0对应的时间;t为温度场瞬态温度T对应的时间是2个常数系数,对于不同材料和是变化的;Tg是玻璃化转变温度(玻璃态化为橡胶态),当T≤Tg-时,就变成弹性性质。
ABAQUS中通过WLF方程可以将任意温度转化到参考温度,系数发生了改变
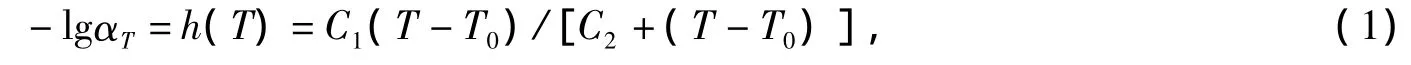
式中C1,C2是针对沥青混合料的不随温度变化的常数。
普适常数Cg1、Cg2与C1、C2的关系为
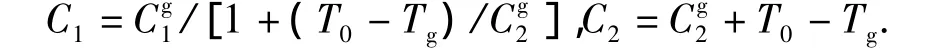
对于沥青混合料,通过松弛试验,按照各种温度下有效的试验结果平移至参考温度T0=-5℃后相对偏差最小的原则进行数值模拟,得到参数C1=38.46,C2=316.35[6]。

图5 有限元模型网络划分图
3 有限元计算模型
3.1 有限元模型的建立
本工程中,有限元模型宽度取1.5 m,长取2.0 m,高度取1.8 m。边界条件为:沿宽度方向两侧取U1=0;在土基底部取U3=0;在行车方向的两侧取U2=0。采用单元类型为二次减缩积分单元(C3D20R),网格划分如图5所示,沥青混合料本构关系选取ABAQUS软件自带的时间硬化蠕变模型,时间硬化模型关系式为

式中 εcr为蠕变值;σcr为蠕变应力;t为荷载累计作用时间;A,m,n为蠕变参数,不同温度下A,m,n取值如表2所示[7],路面结构尺寸如图6所示。
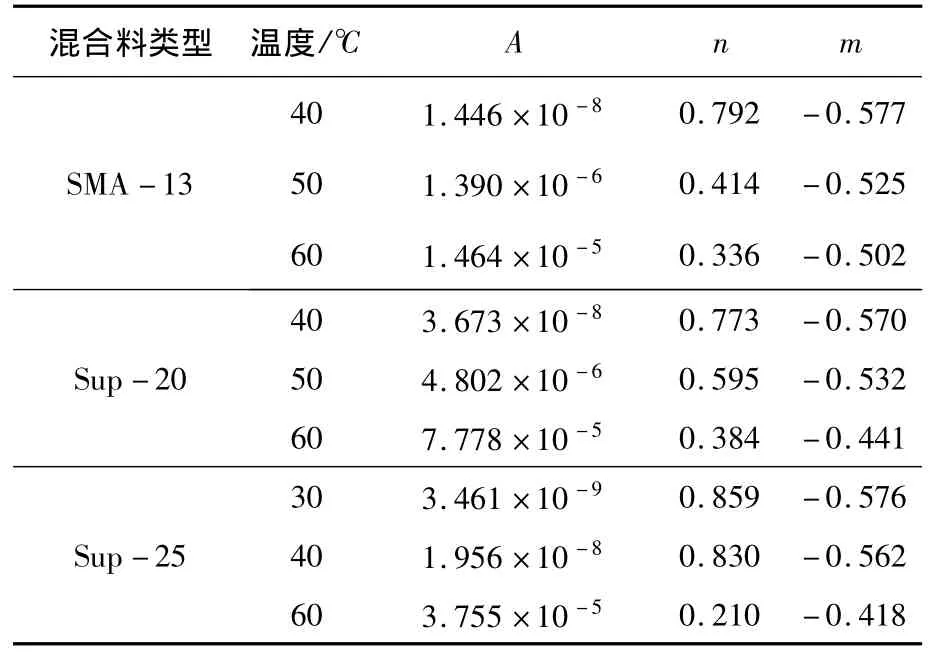
表2 沥青混合料蠕变模型高温参数
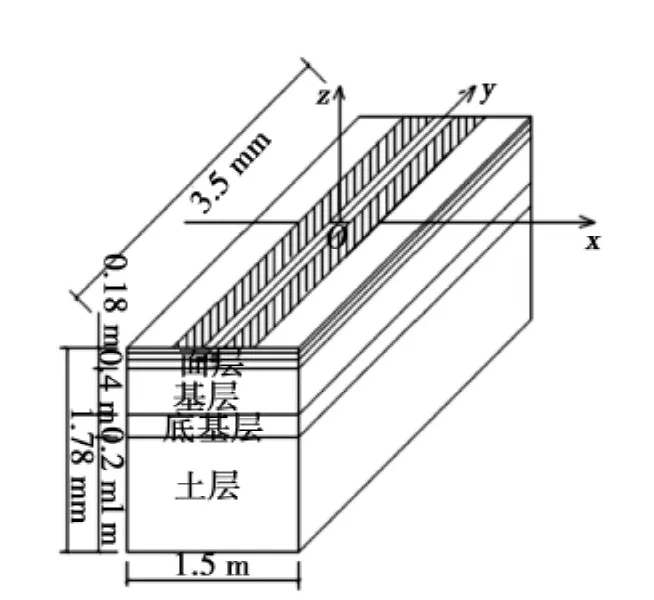
图6 路面结构尺寸图
3.2 温度场模拟
经过前期ABAQUS车辙试算,在时温等效原理的基础上,当平均温度低于14℃时转化成高温作用时间数值非常小,可以忽略。从图2可以看出,车辙计算只需考虑4~11月,因此温度场模拟也只考虑4~11月。根据已建立的有限元模型,代入路面各层材料热物理参数进行路面各层温度场的模拟,路面各层材料热物理参数如表3所示[8]。
通过有限元温度场模拟,7、8月份路面各层1 d 24个时刻的温度变化如图7a)所示,根据图4月平均气温变化情况,假定其它各月每天24个时刻只是基准平均温度按照月平均温度变化,温度变化趋势不变,将温度数据代入有限元温度场模型,得到各个月的温度场模拟结果如图7所示。
从温度场模拟结果可以看出:路面温度变化规律基本与气温周期性日变化规律一致,表面最高温度出现在13:00—14:00,最低温度出现在4:00—6:00;在路面表面,温度场的变化幅度非常明显,日温差也最大;随着深度的增加,最高温度出现的时刻逐渐推后,且温度场随气温变化的变化幅度(日温差)也逐渐减小。

表3 路面各层材料的热物理参数
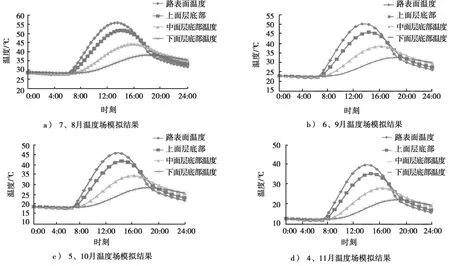
图7 各月温度场模拟结果
4 车辙计算结果
4.1 荷载作用时间计算
本工程实例中,100 kN的双圆均布标准荷载简化为双矩形均布荷载[9],接地宽度B=18.6 cm,轴载P=100 kN,接地压力p=0.7 MPa,轮数nw=4,两轮中心距31.4 cm,例轮胎接地长度L=P/(nwpB)=19.2 cm。
根据行车速度v,一次轮载对路表面的作用时间t1为

由此,当荷载作用次数为N时,车辙处轮载的累积作用时间t为

将式(2)代入式(3),得

由工程资料可知,日交通量为12 989次/d,由文献[10],车道系数为0.45,一个车道当量轴次N=12 989×0.45=5 845次/d,把N值带入式(4)中,即可得到1 d中1个车道处车辙轮载的累积作用时间,然后根据图3不同时段交通量变化情况可以得到1 d不同荷载累积作用时间,以7月份为例,不同时段荷载作用时间如表4所示。
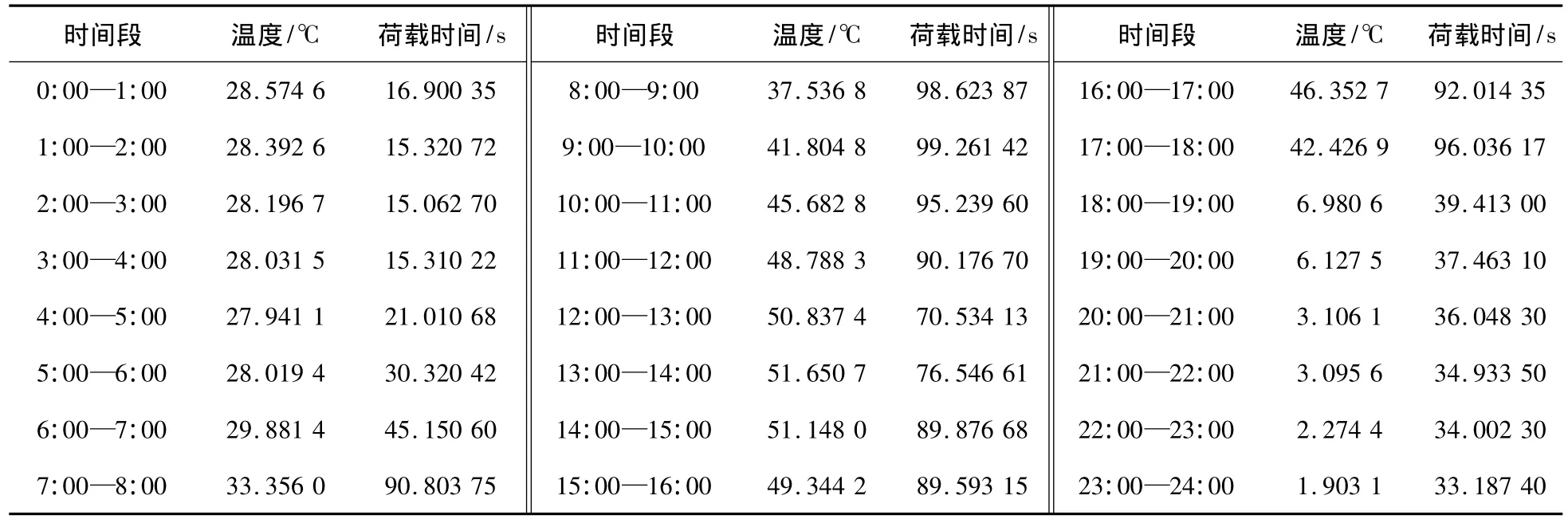
表4 7月份上面层各时段荷载作用时间
4.2 时温等效转化
将C1、C2值代入式(1),得到针对沥青混合料的时温转化方程为
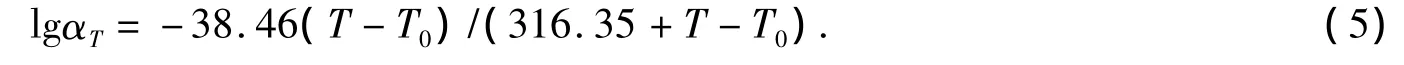
依据温度场模拟结果,以路面上面层为例,利用式(5)将表3中荷载时间转化为50℃温度下荷载作用时间如表5所示。7月份累积作用时间计算值为581.54 s,同理求得中面层转化为40℃时的累积作用时间为1 704.28 s,下面层转化为40℃时的累积作用时间为397.98 s。
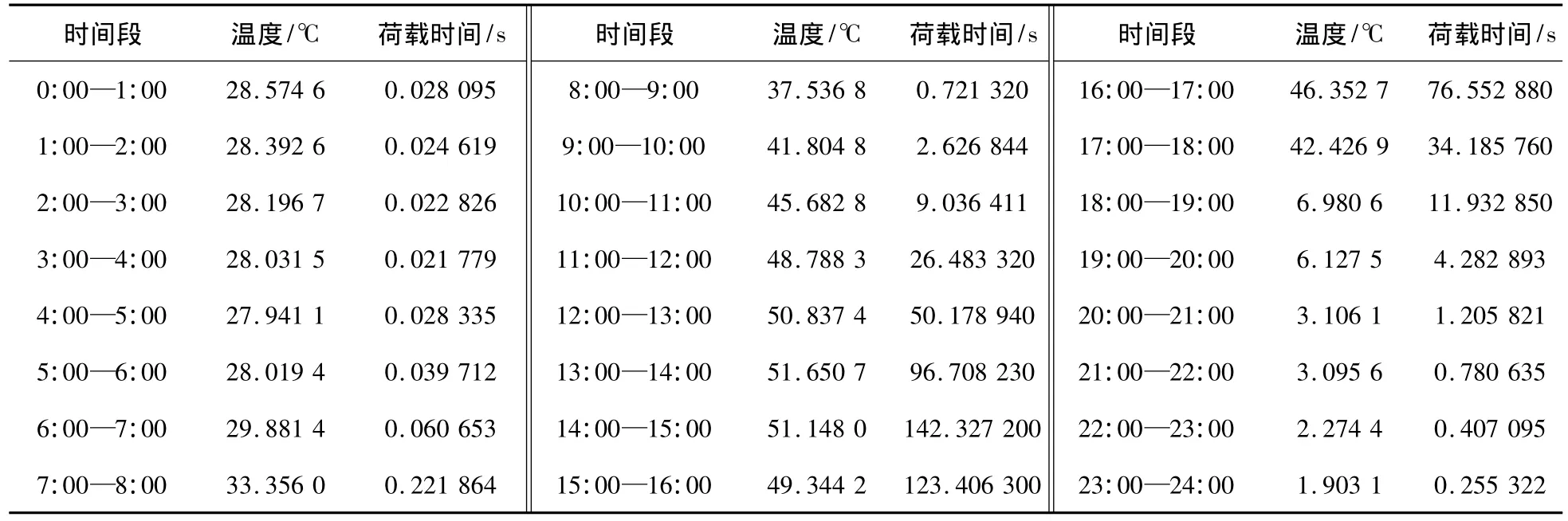
表5 7月份上面层各时段荷载时间转化为高温50℃作用下的时间
同理求得其它各个月份转化成高温下的累积作用时间,5 a各个月份的累积作用时间如表6所示。
由表4可知,由时温等效转化可以看出,4月份和11月份转化成高温作用时间结果很小,因此在车辙计算中不需要考虑1、2、3和12月份,一年按8个月计算荷载累积作用时间来计算车辙量。这也符合实际观测现象,车辙主要发生在高温季节,寒冷季节基本上不产生车辙,春秋季节产生车辙也比较小。
4.3 车辙最终计算结果
鉴于ABAQUS中,在分析上中下面层时时间的输入是一致的,因此有必要再次利用式(4),以上中下面层作用时间相同为前提,将不同时间下不同温度作用转化成相同时间下不同温度作用。以上面层1 446.81 s为标准,中面层40℃下4 270.953 2 s换算成1 446.81 s时等效温度为43.91℃,下面层40℃下982.604 s换算成1 446.81 s时等效温度为38.62℃。上面层和下面层的等效温度分别为50℃和38.62℃,在车辙计算时面层材料蠕变参数A,m,n分别取50℃和40℃的数值,中面层等效温度43.91℃采用在40℃和50℃线性插值的方法来获取材料的蠕变参数。
通过上述有限元计算模型,车辙计算结果如下:5 a标准轴载作用下车辙深度为10.87 mm,超载100%作用下车辙深度为13.54 mm,超载200%作用下车辙深度为14.25 mm。
5 结论
1)通过时温等效原理对荷载作用时间的转化,恒温作用下车辙预估方法预估5 a车辙深度,计算结果符合实际观测数据。2)冬季基本上不产生车辙,春秋季节产生车辙很小,车辙主要发生在高温季节。3)由于超载限制了车辆的行驶速度,路面车辙深度大大增加,对于实际工程,沥青混合料抗车辙性能应根据车辆轴载比例不同而制定不同的标准。
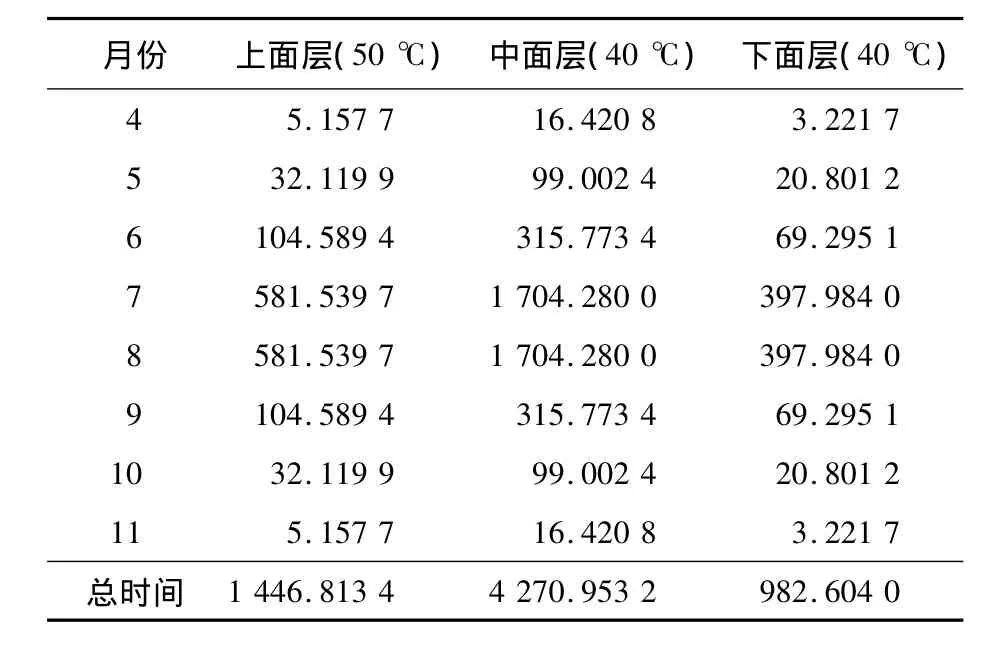
表6 5 a各面层高温作用时间 s
[1]沈金安.沥青及沥青混合料路用性能[M].北京:人民交通出版社,2003.
[2]张登良,李俊.高等级道路沥青路面车辙研究[J].中国公路学报,1995,8(1):23.
[3]李辉,黄晓明,张久鹏,等.基于连续变温的沥青路面车辙模拟分析[J].东南大学学报:自然科学版,2007,37(5):915-920.
[4]赵培仲,文庆珍,朱金华.时温等效方程的研究[J].橡胶工业,2005,52(6):142 -145.
[5]张肖宁.沥青与沥青混合料的粘弹力学原理及应用[M].人民交通出版社,2006.
[6]彭彬.沥青路面低温开裂数值模拟与参数分析[D].南京:东南大学,2009.
[7]李凌林,黄晓明,李昶.沥青混合料动稳定度控制在山区公路中的应用[J].东南大学学报:自然科学版,2010,40(3):599-603.
[8]付凯敏.沥青路面结构车辙模拟及抗车辙性能研究[D].南京:东南大学,2007.
[9]俞文生,李昶.陡坡路段沥青路面车辙特性分析[J].重庆交通大学学报,2009,28(6):1028-1032.
[10]中交公路规划设计院.JTG D50—2006 公路沥青路面设计规范[S].北京:人民交通出版社,2006.
