新型SVPWM 5电平逆变器算法及过调制研究

杨泰朋，李高峰，戴鹏

（中国矿业大学 信息与电气工程学院，江苏 徐州221008）

1 引言

经过几十年的研究发展，空间矢量PWM技术已经广泛应用于工业的中高压系统中[1]。SVPWM 技术由于其直流侧电压利用率高、动态响应快速、 输出电压畸变小及易于数字化实现的特点在电机控制以及功率变换中得到广泛应用。

矢量脉宽调制广泛应用于电压源型逆变器，因为它可以产生不同等级和不同频率的输出电压，在线性调制区内，最大电压为6 拍波值的90．7%。空间矢量脉宽调制技术（SVPWM）在两电平逆变器特别是其过调制控制中得到广泛应用。

SVPWM 对于多电平逆变器来说也是很好的控制策略，因为：1）可以有效改善直流电压利用率，降低开关损耗和谐波畸变率（THD）；2）可以用数字信号处理器（DSP）进行控制，并且可以优化开关作用顺序。

多电平逆变器SVPWM 的控制很复杂，其复杂性来源于对非线性过调制区域的控制，本文提出了基于6 拍基波的过调制区域控制[2]的控制策略。 下面我们先简单介绍此领域的近期研究成果。

文献[3]提出了在线性调制比下的控制，但是其没有提出对非线性过调制区域的控制，文献[4]提出了基于叠加原理的SVPWM 过调制算法，该算法与传统两阶段过调制算法相比较，易于数字化实现，但是不能直接应用到多电平逆变器中。 所以随着电平数n（n＞3）的增加，SVPWM 的控制复杂性和计算量都会增加。

本文阐述了一种新型简化的SVPWM 逆变器控制算法，并实现了对过调制区域的控制，本方案突出的优点如下：

1）易于判断出矢量的坐标，基于两电平计算时间和分配开关顺序，可以拓展至n 电平（n＞3）；

2）在过调制区域内，只需要优化矢量位置，从而得到对应的开关状态和作用时间，简单，易实现，随着电平数n 的增加，这种过调制方法同样适用。

本文将这种新型调制算法应用到5 电平NPC 逆变器中，并在Matlab 仿真环境中实现了该算法，并且进行了实验，仿真和实验结果验证了算法的有效性。

2 5 电平逆变器结构及原理

5 电平逆变器的拓扑结构如图1所示，每相桥臂有5 种输出状态。 以A 相为例，其桥臂有8 个开关器件，每一个开关都反并联一只续流二极管。 还有6 个钳位二极管、4 个均压电容，由于直流侧电压为Vdc，所以平均每个主开关器件所承受的电压为Vdc/4。 当Sa1，Sa2，Sa3，Sa4同时导通时，该相输出端电压等于P2点电位为Vdc/2；当Sa2，Sa3，Sa4，Sa′1同时导 通，该相输 出 端 电压等于P1点电位为Vdc/4；当同时导通时，该相输出端电压等于O 点电位为0；当同时导通时，该相输出端电压等于N1点 电 位 为-Vdc/4；当Sa′1，Sa′2，Sa′3，Sa′4同 时 导通时，该相输出端电压等于N2点电位为-Vdc/2[5]。

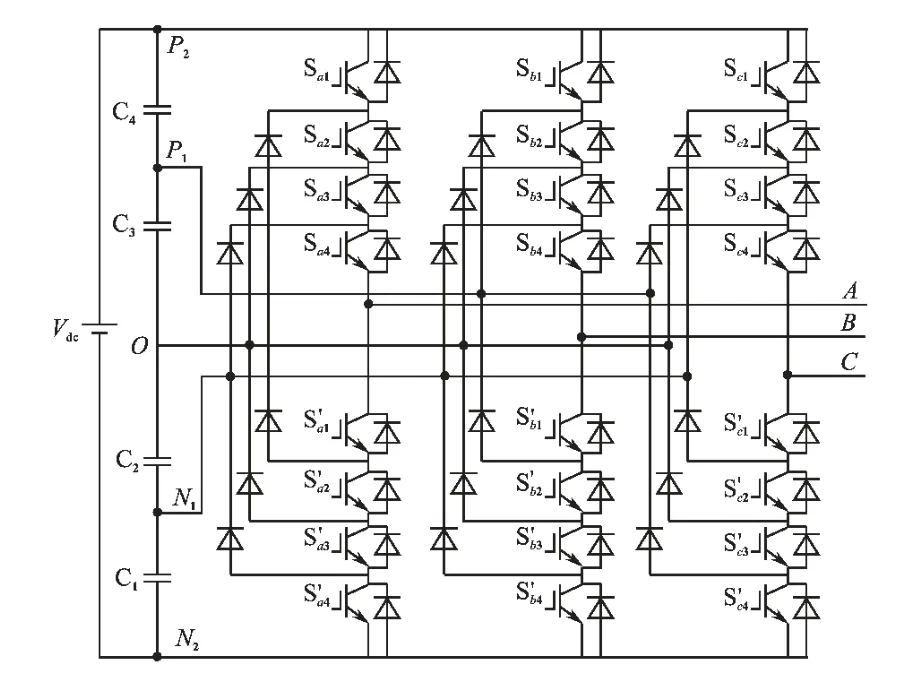
图1 二极管钳位5 电平逆变器结构图Fig.1 Structure of diode clamped five-level inverter

5 电平逆变器每相有5 种开关状态，共有53=125 种开关状态。所以，5 电平逆变器可以输出125 种电压矢量。 将这125 种电压矢量分为零电压矢量、 小电压矢量、 中电压矢量和大电压矢量。 图2为α-β 坐标系下各个电压矢量的分布图[5]。

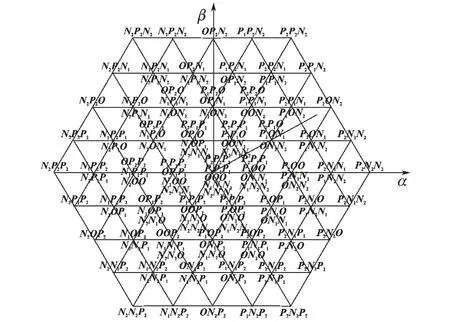
图2 α-β 坐标系下5 电平逆变器空间电压矢量图Fig.2 Space voltage vector diagram of five-level inverter in α-β

3 新型SVPWM 算法

在线性调制区内，定义调制系数mi=v1/v1six-step[6]，v1为调制器基波电压的峰值，v1six-step为在6 拍调制下基波电压的峰值。 对于NPC 结构的逆变器来说，v1six-step=（2/π）Vdc。

本文的控制算法中，将六边形分为6 个扇区，下面以第1 扇区为例讨论此新型控制算法。 如图3所示，第1 扇区被分割成16 个小三角形△j（j=0～15），v*是幅值为|v*|的矢量，其与α 的夹角为γ，在小三角形中建立了新的坐标系（α0，β0），并用vs表示有相同顶点位置的矢量，这样就把5 电平控制归化到2 电平中计算，从而能很方便计算出矢量作用时间：

图3 第1 扇区两电平小三角形分区图Fig.3 The two-level triangle partition map of the first sector

当k1=2，k2=1 时，矢量落在△6和△7所组成的菱形内，如图4所示，具体落在哪个三角形中将由下式决定：

如 果vβi≤vαi，矢量顶点P落在△6中，所以在三角形0，1，3，4，6，9，11，13，15 中的判断表达式为

如 果vβi＞vαi，矢量顶点P落在△7中，那么在小三角形2，5，7，10，12，14 中的判断表达式为

图4 区域划分图Fig.4 Sector distribution figure

以上完成了把5 电平归化到两电平的工作，接着只要求出矢量作用时间就能实现对5 电平逆变器的SVPWM 控制。 具体步骤如图5所示。

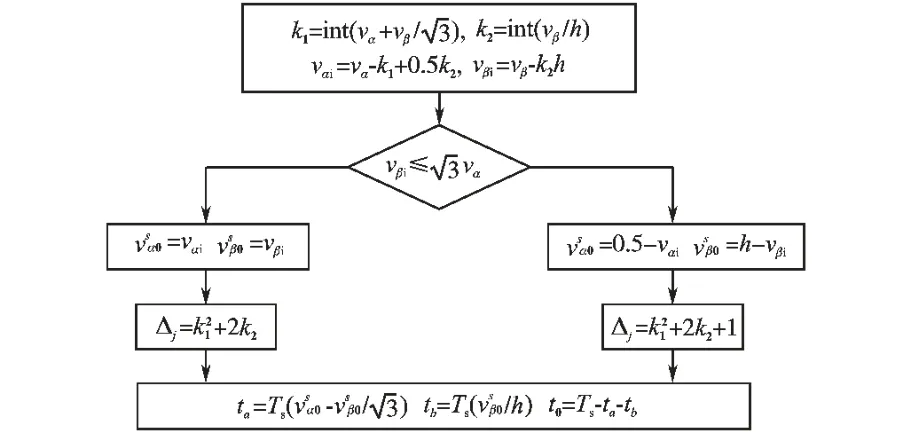
图5 逆变器控制流程图Fig.5 The control flowchart of inverter

4 过调制区域的控制

借鉴Holtz[7]的思想，线性调制区与过调制区Ⅰ之间的临界调制比为最大线性调制比，调制系数Mi＝0.907；过调制区Ⅰ与过调制区Ⅱ之间的临界调制比对应实际电压矢量为正六边形轨 迹 时 的 调 制 比，根 据Fourier 分 解[5]可 以 得到M2＝0.953 5[8]。

4.1 过调制区Ⅰ（0.907≤Mi＜0.953 5）

在过调制区Ⅰ内，采用调整作用时间的方式，而不是对矢量进行调整，来实现对过调制区域的控制。 如图6所示，当αt≤γ＜π/3-αt，此时矢量移动在六边形轨迹上，而在剩下的部分，矢量沿着圆形轨迹移动。

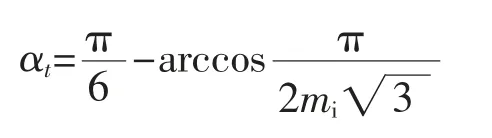
对于每个矢量，αt和mi为确定量，所以在每个开关周期不需要再计算它们的值，在很大程度上简化了计算。 此时的过调制控制步骤如图7所示。

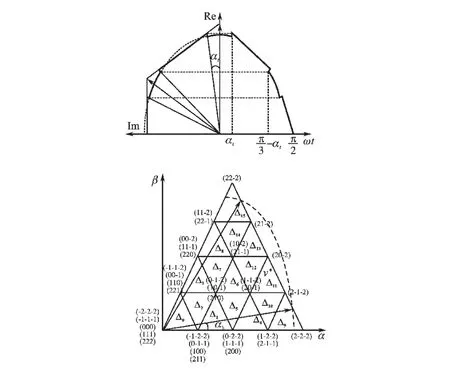
图6 过调制Ⅰ区矢量规划图Fig.6 Vector in the overmodulation sector Ⅰ

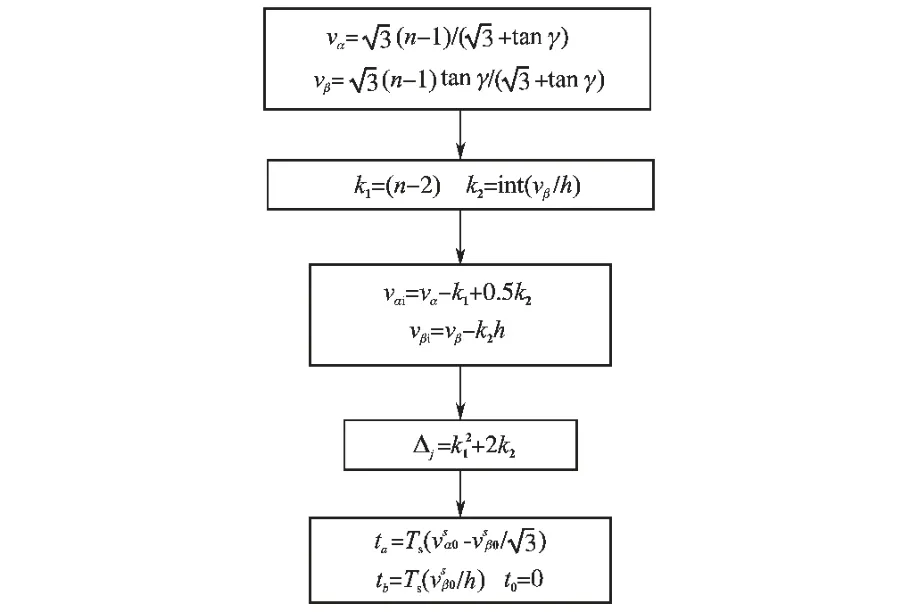
图7 过调制Ⅰ区控制流程图Fig.7 The flowchart of control in overmodulation sectorⅠ

当0≤γ＜αt和π/3-αt≤γ＜π/3 时，如图6所示，矢量顶点P 可以位于△9~△15中，这里定义L=（mi-0.907）/0.046 5 为实际伏秒损耗与最大伏秒损耗的比值作为时间的调整参数。 可以根据前文流程得出时间ta，tb，t0。

1)若矢量顶点P 在△9，△11，△13和△15中，时间修正的表达式为

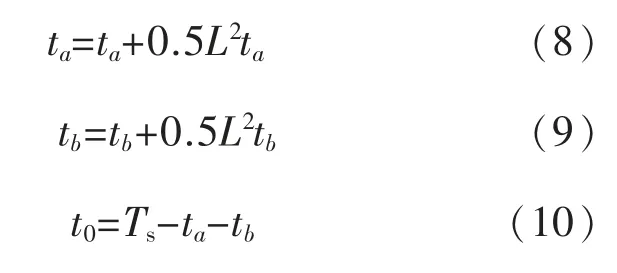
2）若矢量顶点P 在△10，△12，△14中，时间修正表达式为

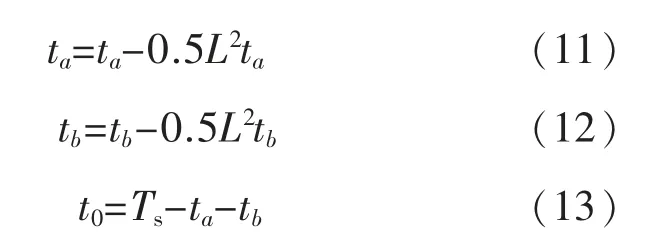
4.2 过调制Ⅱ区（0.953 5≤Mi＜1）

在过调制Ⅱ区的分析步骤跟Ⅰ区类似，其矢量轨迹图如图8所示，参照在过调制Ⅰ区的方案，对过调制Ⅱ区的时间进行调整，定义αh=10.5（1.05-1/mi）。

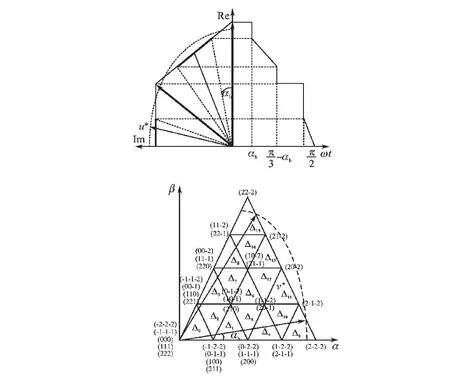
图8 过调制Ⅱ区矢量规划图Fig.8 Vector in the overmodulation sector Ⅱ

1）当αh≤γ＜π/3-αh时，调整步骤同调制Ⅰ区的流程图。

2）当0≤γ＜π/6 时，ta=Ts，tb=0 ，t0=0。

3）当π/6≤γ＜π/3 时，ta=0，tb=Ts，t0=0。

5 仿真研究

根据以上三相5 电平空间电压矢量理论算法，在Matlab/Simulink 仿真环境下建立了其模型，进行了仿真。 仿真参数为：Vdc=1 000 V，输出频率f=50 Hz，直流侧电容为C=2 200 μF，负载R=10 Ω，L=10 mH，系统开关频率为f=5 kHz。

输出得到的逆变器线电压和负载相电流波形如图9所示。

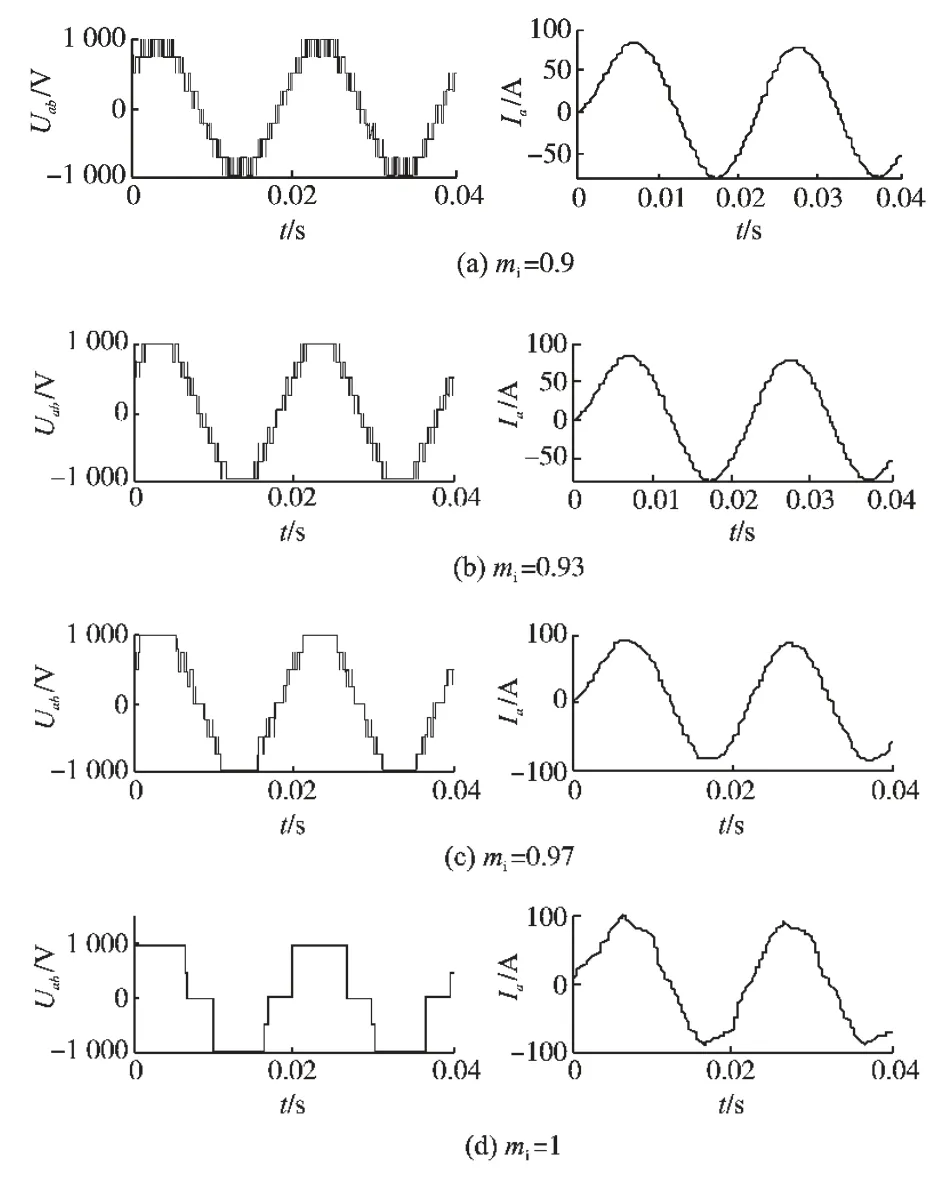
图9 不同调制度下的仿真波形Fig.9 Simulation waveforms in different modulation index

由表1可以看出，随着调制度的增加，谐波畸变率（THD）也在增加，当mi=1 时，THD 达到最大，本文提出的在过调制区域内的算法，谐波畸变率在从线性调制区向过调制的过渡过程中变化较小，可行性很高。

表1 不同调制度下的THD 值Tab.1 THD index in different modulation

6 实验验证

实验平台的逆变器拓扑结构是二极管钳位式5 电平结构，实验控制器由DSP 和FPGA 组成。 DSP 采 用TI 公司的TMS320F28335 高 性 能数字信号处理器，其CPU 主频可以达到150 MHz，DSP 主要用来实现算法，开关频率为5 kHz，逆变器输出频率为50 Hz；FPGA 主要用于完成死区产生、故障保护、脉冲扩展等操作，实验使用Xilinx 公司Spartan3 系列的XC3S400 FPGA，其中死区时间为5 μs；主电路直流侧采用4 个1 800 μF/400 V 的电解电容，开关管采用IRF840 型MOSFET，驱动芯片采用HCPL316；吸收电路采用RCD 型，电阻为10 Ω，电容为2 μF 的无感电容，二极管采用MUR860超快恢复二极管；负载选择Y 型连接的3 项对称阻感负载，电感值为10 mH，电阻值为10 Ω，直流侧电压为100 V。 不同调制度下的线电压实验波形如图10所示。

图10 实验波形Fig.10 Experimental waveforms

由实验波形可以看出，调制比为0.9 时对应线性调制状态，此时电压畸变很小； 调制比为0.93 时处于过调制区Ⅰ内，线电压波形出现较小畸变； 调制比为0.97 时处于过调制区Ⅱ内，线电压波形畸变较严重； 当调制比为1时，线电压为6 拍波，系统进入了6 拍波工作状态。

7 结论

本文分析了一种新型SVPWM 算法，这种算法适用于多电平逆变器的控制，并且分析了其在过调制区域的控制，通过实验和仿真可以看出波形从5 电平线性调制逐渐向过调制变化的过程，在调制度达到1 时，波形是6 拍阶梯波。 而且经过FFT 分析，同文献[9]的过调制算法进行比较，见表1，此算法的电压谐波含量较低。 所以不管在线性调制还是过调制区，此算法的实用性很强，而且大大提高了电压利用率。

[1] 李永东.高性能大容量交流电机调速技术的现状及展望[J].电工技术学报，2005，20（2）：1-10.

[2] 张立伟.基于基波电压幅值线性输出控制的SVPWM 过调制新算法[J].中国电机工程学报，2005，25（19）：12-18.

[3] Gopinath A，Aneesh Mohamed A S，Baiju M R.Fractal Based Space Vector PWM for Multilevel Inverters-A Novel Approach[J].IEEE Transactions on Industrial Electronics，2008，55（11）：1230-1237.

[4] 樊扬，瞿文龙，陆海峰，等.基于叠加原理的SVPWM 过调制方法[J].清华大学学报，2008，48（4）：461-464.

[5] Khajehoddin S，Bakhshai A，Jain P.A Simple Voltage Balancing Scheme for M-level Diode-clamped Multilevel Converters Based on a Generalized Current Flow Model[C]∥Power Electronics，IEEE Transactions on，2008，23：2248-2259.

[6] Quan Hengli，Zhang Gang.Study of a Novel Over-modulation Technique Based on Space-vector PWM[C]∥Power Electronics，IEEE International Conference on，2011，9：295-298.

[7] Holtz J.Pulse Width Modulation-a Survey[J].IEEE Transaction on Industry Electron.，1992，39（6）：410-420.

[8] Holtz J.On Continuous Control of PWM Inverters in the Overmodulation Range Including the Six- step Mode [J].IEEE Transactions on Power Electronics，1993，8 （4）：546-552.

[9] Fortes G O，Mendes M A S，Cortizo P C.Recursive Multilevel Modulation Algorithm for Generalization of the Linear N-step Operation Mode[C]∥IECON 2011-37th Annual Conference on IEEE Industrial Electronics Society，2011，9：1995-1999.