Wilson-Cowan神经网络的概周期解及其稳定性

谢莎莎，黄振坤

(集美大学理学院，福建 厦门 361021)

0 引言

Wilson-Cowan模型是由著名学者Wilson和Cowan于1972年提出[1]，它是用于描述神经网络不同特性神经元群体动力演化的方程.该模型由两个非线性微分方程组成，代表相互作用产生兴奋和抑制的两种神经元群体之间的关系.Wilson-Cowan网络受到许多学者的关注，如文献 [2]通过选择适当的双曲函数并分析参数的取值范围，获得渐近稳定极限环的存在性;文献[3]利用对称特性和庞加莱映射找到周期振动区域的参数空间，证明Wilson-Cowan存在三个或多个周期吸引子;文献[4]研究Wilson-Cowan网络中神经元相互作用产生兴奋或抑制行为，且在周期性输入下对神经元有完全不同的激活或抑制影响.然而对Wilson-Cowan网络在概周期环境下解的存在性和稳定性还没有相关的报道.近年来，Wilson-Cowan神经网络模型在图像处理和联想记忆方面的应用非常广泛，研究其内在动力学性质在神经网络的设计和应用领域具有重要意义.在概周期信号激励下[5-8]，它是否具有唯一的周期或概周期编码，值得探讨.本文应用与文献[6]类似的技巧，利用压缩不动点定理以及Lyapunov泛函方法，给出了一些Wilson-Cowan网络存在唯一概周期解及其指数型稳定的充分条件.

1 预备知识

考虑如下Wilson-Cowan神经网络

其中:x(t)，y(t)分别表示单位时间内神经元兴奋和抑制所占比例，假设x(t)，y(t)是连续的变量，它们取值表示神经元群体处理信息的编码，即状态变量;a(t)，d(t)分别表示兴奋神经元和抑制神经元群体随着时间自然衰变的函数;rx(t)，ry(t)分别表示兴奋和抑制神经元的不响应期;w(t)，b(t)，c(t)，e(t)表示不同神经元群体之间联结的强度，w(t)是自兴奋联结权重，b(t)是从y到x的联结权重，c(t)是从x到y的联结权重，e(t)是自抑制联结权重;I(t)，J(t)表示外部刺激对神经元群体产生兴奋或抑制输入;S(·)表示神经元双曲型的激活响应函数.

进一步，令a(t)，d(t)，rx(t)，ry(t)，w(t)，c(t)，b(t)，e(t)，I(t)，J(t):R→R+是概周期函数，并且满足:

定义1[9]连续函数x(t):R→Rn称为概周期函数，如果对任给的ε〉0，存在一个实数l=l(ε)〉0，使得在每个长度为l(ε)的区间内至少有一个δ=δ(ε)，使得

定义2 设x*(t)=(x(t)，y(t))T是系统 (1)的一个具有初始条件φ*=(x*0，y*0)T的概周期解，如果存在常数λ〉0和M≥1，对于系统 (1)的具有初始条件φ=(x0，y0)的每一个解x(t)=(x(t)，y(t))T满足则称x*(t)是全局指数稳定的．

定义3[9]设Q(t)是定义在R上的n×n连续矩阵函数．线性系统˙x=Q(t)x(t)称为在R上是容许指数二分的，如果存在常数k，l〉0投影算子P以及基础解矩阵X(t)满足

引理1[9]如果线性系统˙x(t)=Q(t)x(t)是容许指数二分的，则概周期系统˙x(t)=Q(t)x(t)+g(t)有唯一的概周期解

引理2[9]假设ci(t)是R上的一个概周期函数，并且n，则线性系统˙x(t)=C(t)x(t)是容许指数二分的，其中C(t)=diag(-c1(t)，-c2(t)，…，-cn(t))．

2 概周期解的存在性与唯一性

首先给出一些本文需要的假设．1)存在常数L〉0，使得双曲激活函数S∈C(R，R)满足:

证明 任取φ =(φ1，φ2)T∈B*，考虑系统

由 a(t)≥ a⊥〉 0，d(t)≥ d⊥〉 0，有根据引理1和引理2，系统 (2)存在唯一概周期解

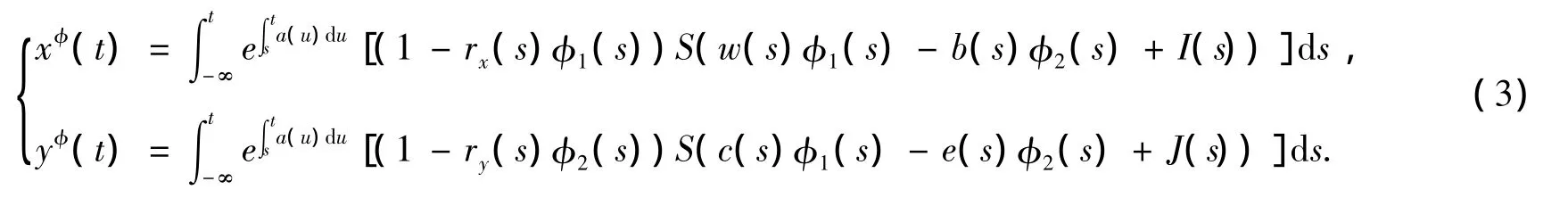
定义映射 F:B*→B，F=(F1(φ)，F2(φ))，其中 F1(φ(t))=xφ(t)，F2(φ(t))=yφ(t)，∀(φ1，φ2)T∈B*．显然是B的闭凸子集．

下面首先证明F将B*映射到B*，结合假设1)，2)，获得

注意到，0〈R〈1，这意味着F是一个压缩映射．据不动点定理，则存在唯一的不动点φ*∈B*，使得Fφ*=φ*．故φ*是系统 (1)在B*中唯一的概周期解，定理1证毕．

3 概周期解的指数稳定性

定理2 若条件1)、2)成立，则系统 (1)在B*中存在唯一全局指数型稳定的概周期解．

证明 由定理1，系统 (1)存在唯一的概周期解(x*(t)，y*(t))T∈B*．令(x(t)，y(t))T是系统 (1)具有初始条件ψ=(x0，y0)T的解．令X(t)=x(t)-x*(t)，Y(t)=y(t)-y*(t)，则

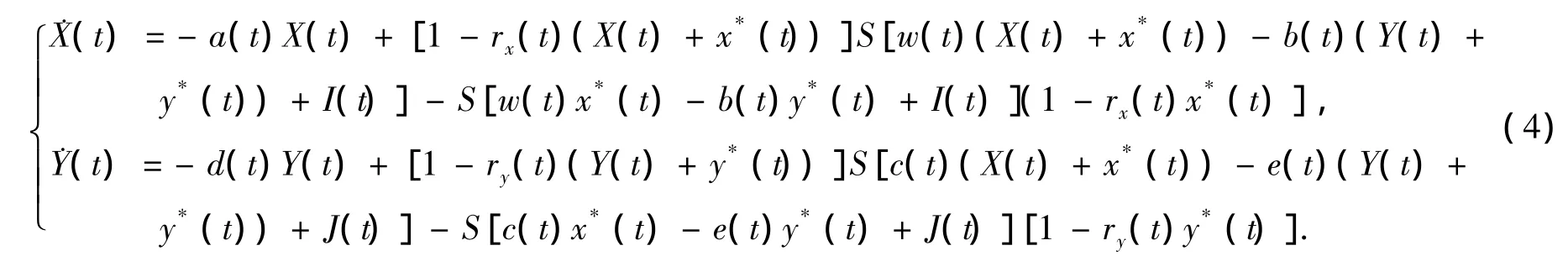
构造两个辅助函数

由Γ1(ξ)、Γ2(ξ)是[0，+∞)上的连续函数，可得，

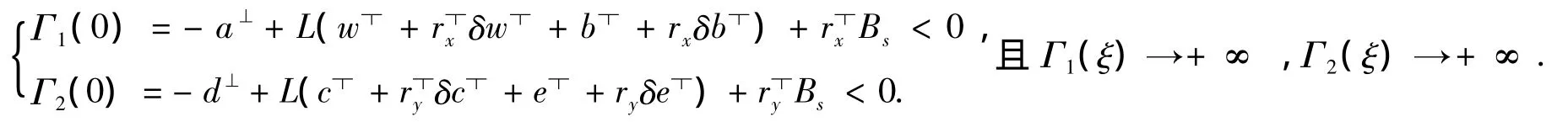
当 ξ→ +∞，可以选择一个正常数 λ ∈[0，λ0]，λ0=min{λ1，λ2}，Γ(λ1)〈 0，Γ(λ2)〈 0，使得

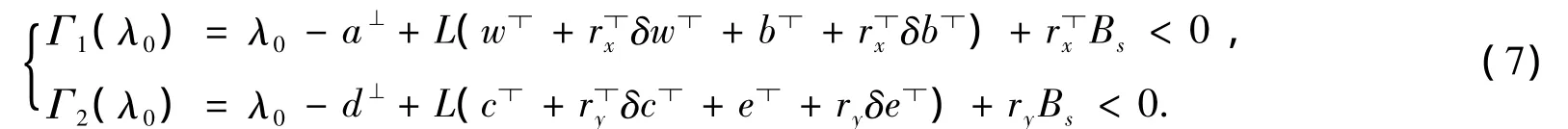
[1]WILSON H R，COWAN J D.Excitatory and inhibitory interactions in localized populations of model neurons[J].Biophys，1972，12(1):1-24.

[2]MONTEIRO L H A，BUSSAB M A，CHAUI BERLINCK J G.Analytical results on a Wilson-Cowan neuronal network modified model[J].Theor Biol，2002，219:83-91.

[3]DECKER R，NOONBURG V W.A periodically forced Wilson-Cowan system with multiple attractors[J].SIAM J Math Anal，2012，44(2):887-905.

[4]NOONBURG V W，BENARDETE D，POLLINA B.A periodically forced Wilson-Cowan system [J].SIAM J Appl Math，2003，63(5):1585-1603.

[5]LIU B W，HUANG L H.Almost periodic solution of shunting inhibitory cellular neural networks with time-varying delays[J].Appl Math Lett，2007，20(1):70-74.

[6]张若军，王林山.具有分布时滞的细胞神经网络的概周期解 [J].数学物理学报，2011，31A(2):422-429.

[7]HUANG Z K，WANG X H，MOHAMAD S.Self-excitation of neurons leads to multiperiodicity of discrete-time neural networks with distributed delays [J].Sci China Inf Sci，2011，54(12):305-317.

[8]HUANG Z K，MOHAMAD S，WANG X H，et al.Convergence analysis of general neural networks under almost periodic stimuli[J].Int J Circ Theor Appl，2009，37(6):723-750.

[9]何崇佑.概周期微分方程 [M].北京:高等教育出版社，1992.

[10]LI Y L，MENG H，ZHOU Q Y.Exponential convergence behavior of shunting inhibitory cellular neural networks with time-varying coefficients[J].Journal of Computational and Applied Mathematics，2008，216(1):164-169.