可倾斜式车辆转向机构的设计*

王 凌，何 涛，孙 策，于丛赫，张 宇

(北京交通大学机械与电子控制工程学院，北京 100044)

1 前言

传统转向机构的车辆在转弯过程中往往存在因过弯速度较高而造成的转向不足，甚至造成车辆侧翻的安全隐患。为避免该现象的发生，需在过弯前采取制动，但这样势必会造成油耗的增加。从环保节能的角度出发，现代车辆急需一种新型转向机构。

2 可倾斜式车辆转向机构的提出

笔者提出了一种可以提高车辆过弯速度并保证安全性的新型可倾斜式车辆转向机构，其原理如图1、2所示。

图1 直行状态

图1为车辆直行时转向机构的状态。车辆进行转向时，在这种新型可倾斜转向机构的作用下，车轮会带动车身向弯道内侧倾斜一定角度，如图2所示。此时车身重力和地面给予车轮的支持力的合力便会提供除地面与轮胎的摩擦力之外的向心力，从而令车辆可在保证安全性的前提下，以更高的速度过弯，从而避免了入弯前的减速或者制动。

图2 转向状态

3 可倾斜式车辆转向机构的功能要求

以上阐述了可倾斜转向机构工作的基本原理。为在车辆进行水平偏转时实现车身向弯道内侧的倾斜，可倾斜转向机构还应同时实现车辆的水平偏转和沿车身轴线方向的倾斜。针对这两大功能的要求，给出初步实现方法。

3.1 水平偏转

采用传统的梯形转向机构实现车辆水平偏转。梯形转向机构由车架前端、横拉杆、梯形臂、控制杆组成。通过方向盘的转动带动控制杆，控制杆末端位移输入到转向梯形的一顶点，从而实现梯形形状的变化，最终使车辆前轮做符合条件的偏转。

3.2 沿车身轴线方向的横滚倾斜

三角支架、锥齿轮、T形杆组成了实现车身沿轴线方向的横滚倾斜。由方向盘两侧的前后推拉带动一组锥齿轮运动，传递给T形杆，T形杆再带动2个三角支架上下移动，从而实现车辆的倾斜。

由图3可知，车辆的前转向轮是通过同时完成水平面的转动和竖直面的上下平动来达到可倾斜转向的目地。但转向机构是通过对左、右转向轮不同转向角之间的合理匹配来保证汽车按理想的轨迹进行运动的机构。为避免转向时路面对汽车的附加阻力和轮胎的过快磨损，转向机构必须保证所有车轮均做纯滚动。这对转向机构各部分的尺寸提出了精确要求。

图3 转向机构机构简图

4 可倾斜式车辆转向机构的数学模型

从上文提出的转向机构结构简图可知，因车轮总与地面接触，故所有车轮的轴线总是同时交于一条直线。将这种三维情况投影到二维平面可以发现，可倾斜式车辆转向机构依然满足阿克曼转向原理中对于所有车轮的轴线必须相交于一点的要求。故得出结论，仍可根据阿克曼转向原理进行可倾斜式转向机构的结构设计。下面将从数学角度，建立可倾斜式车辆转向机构的数学模型。

4.1 理论曲线数学模型方程

建立如图4所示的平面转向模型，忽略转向横拉杆CD，车轮的转动直接带动转向梯形臂的转动。以此研究转向梯形臂延长线的交点O在任意转角位置时的变化曲线，该曲线即为平面理论转向特性曲线。

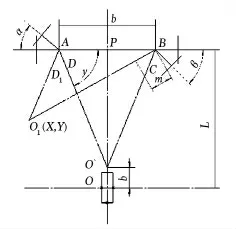
图4 理论转向模型

梯形底角γ的确定:

在△O′AP中:

式中:L为汽车轴距;b为汽车论据;d为汽车直线行驶时梯形臂延长线交点O的位移。

阿克曼原理的纯滚动要求:

α和β分别为左右两轮转向角。

梯形臂的参数方程矩阵为:

可得矩阵:

解得:

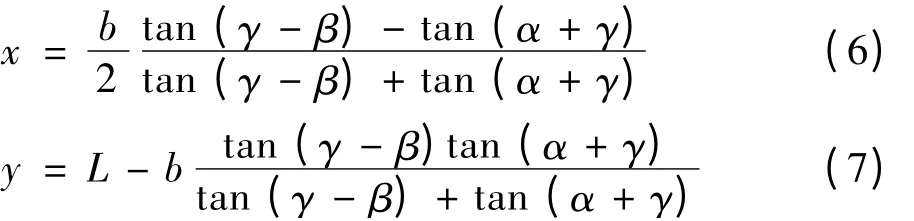
4.2 实际曲线数学模型

加上转向横拉杆CD，如图5所示。车轮转向带动梯形机构的变化，梯形臂延长线的交点O的位置变化曲线为平面转向梯形机构实际转向特性曲线。图中ABCD为汽车直行时的转向梯形，ABC1D1为左前轮转向角为α时梯形的位置。

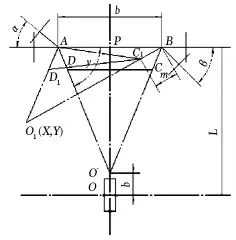
图5 实际转向模型

梯形臂的参数方程矩阵为:

可得矩阵为:

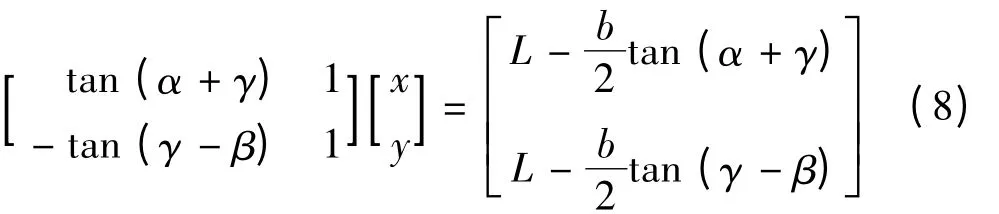
由几何关系可得:

求解∠BAC1:

由余弦定理可得:

由正弦定理可得:

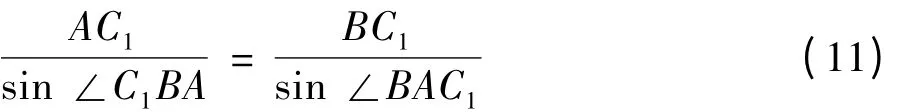
求解∠C1AD1:

由余弦定理可得:

解得:

在实际过程中，内侧轮有最大转向角βmax:

根据上述通过建模和计算得到的理论和实际的转向特性曲线计算方程，需进一步利用Matlab原件和C语言进行编程绘制出理论和实际的转向特性曲线，从而更加直观的指导新型可倾斜式车辆转向机构的结构设计。

5 数学模型的计算和编绘

利用Matlab软件和C语言程序对建立的数学模型进行计算和编绘，将转向梯形机构的研究简化成转向三角形顶点轨迹的研究，通过理想曲线和实际曲线的对比，验证提出的可倾斜式转向机构满足阿克曼原理，同时通过控制变量法得出理论曲线与实际曲线的相似度和梯形臂长度m和梯形底角γ的关系。

5.1 Matlab验证可倾斜式转向机构

从图6、7中实线为实际转向特性曲线，虚线为理论转向曲线，可以看出在转向角度β≤γ-arccos时，即图6，实际曲线与理论曲线非常相近，但当转向角度β超过βmax时，即图7，实际曲线将不再符合理论曲线，所以得出，在转向角度β＜βmax的情况下，可倾斜式转向机构满足阿克曼原理。

图6 理论曲线和实际曲线对比(m=0.1b，β=0.6，γ=0.7)

图7 理论曲线和实际曲线对比(m=0.1b，β=0.9，γ=0.7)

5.2 Matlab分析理论曲线与实际曲线

由图8可知，在控制梯形臂m不变，最大转向角度小于βmax的情况下，通过改变梯形底角γ的值用Matlab画出图8图像，从图中可以发现随着梯形底角γ的不断增大，实际曲线与理论曲线差异越来越大，所以得出结论，梯形底角γ越小，理论曲线与实际曲线越接近。

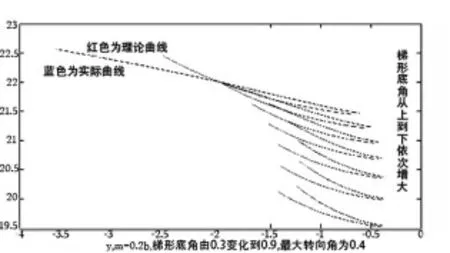
图8 理论曲线与实际曲线的相似度(m=0.b，β=0.4，γ=0.1:0.1:0.9)

在控制梯形底角γ不变，最大转向角度小于βmax的情况下，可通过改变梯形臂m的长度，用Matlab画出图9图像，从图9中可以看出，随着梯形臂的增大，实际曲线越偏离理论曲线，所以梯形臂m越小实际曲线越与理论曲线吻合。

图9 理论曲线与实际曲线的相似度

通过对参数梯形臂m与梯形底角γ的比较，得出如下结论:在满足最大转向角的情况下，梯形臂m越大，梯形底角γ越小，实际曲线就越接近理论曲线，同时可倾斜式转向机构就越满足阿克曼原理。

5.3 C语言程序求出转向机构的尺寸最佳数值

在Honda中国节能竞技大赛的参赛用车已有的转向机构机构的尺寸基础上，套用上述结论，通过C语言编程求出了使实际曲线与理论曲线吻合情况最好的梯形臂长度m和底角γ的最优值。C语言程序截图如图10所示。

图10 C语言程序运行结果

由程序计算结果可知，在主销中心距b=0.4 m，轴距L=2 m的情况下，得到满足不同最大转向角的梯形臂长度m和底角γ的最优值，结果如表1所列。

表1 机构最优尺寸

6 可倾斜式车辆转向机构的建模和仿真

综上所述，针对于Honda中国节能竞技大赛的参赛车辆，选用最大转向角为45°时的梯形臂和底角的最优值，并根据相关公式计算出其他关键尺寸的数观察模值，使用SolidWorks软件对可倾斜式车辆转向机构进行设计和建模，得到三维模型如图11所示。观察模型可以发现，这套可倾斜式车辆转向机构具有操作简单，工作可靠的优点，可实现初期提出的功能要求。在保证安全性的前提下，提高车辆的过弯速度。作为Honda中国节能竞技大赛的参赛用车，还在节省油耗方面有很大的帮助。

图11 转向机构三维模型

7 结语

考虑到传统车辆转向机构在高速过弯方面的缺陷，提出了新型的可倾斜式车辆转向机构，增加了车辆在前进方向的横滚自由度，在保证安全性的前提下提高了车辆的过弯速度，减少了在过弯前制动带来的额外油耗。并建立转向机构的数学模型，利用Matlab程序和C语言程序进行计算和编绘，得到了后期机构设计所依托的结论和最优参数。针对Honda中国节能竞技大赛的参赛用车，利用SolidWorks软件建模，得到倾斜式车辆转向机构的三维模型。故可倾斜式车辆转向机构在改善车辆过弯速度，减少油耗方面既有一定前瞻性，又有实际操作的可行性，给未来车辆的转向机构设计提供了一种新的方向。

［1］ 孟 刚.车辆的转向特性与阿卡曼转向原理的分析［J］.机械研究与应用，2007(4):36-37.

［2］ 陈朝阳，张代胜.汽车转向梯形最优化设计［J］.安徽工学院学报，1982(3):28-36.

［3］ 蔡世芳.汽车转向机构的数学模型及优化设计［J］.汽车工程，1986，8(1):64-68.

［4］ 周全申.车辆转向机构设计与分析［J］.河南工业大学学报(自然科学版)，2006(4):60-66.

［5］ 姚明龙，王福林.车辆转向梯形优化设计及其求解方法的研究［J］.机械设计与制造，2007(5):24-26.

［6］ 彭红星.基于Pro/Engineer的车辆转向梯形机构优化设计［J］.机械研究与应用，2005(3):74-75.

［7］ 夏建满.基于ADAMS的车辆悬架转向系统建模与仿真［J］.机械研究与应用，2009(3):34.

［8］ 张芬娜，崔学政，袁永丽.工程车辆的转向模式及运动学分析［J］.机械研究与应用，2009(1):22-24.

［9］ 许宝彬，孟俊焕，赵鲜花.拖拉机转向梯形机构的优化设计研究［J］.机械研究与应用，2006(3):66-69.