齿轮传动可靠性预测之马尔科夫模型*

朱春伟，任传胜

(中国科学技术大学 工程科学学院，安徽 合肥 230027)

1 问题的提出

齿轮传动失效是一个非常严重的问题。如能及早的发现齿轮的失效趋势，就可以更好的对其进行设备维护维修，避免危险事故的发生，因此对齿轮的可靠性预测是非常必要的。常见的齿轮的失效形式有:齿面点蚀、齿面磨损、齿面胶合、齿面变形、轮齿折断等。这些失效形式相互影响作用，关系复杂，存在一定的模糊性。目前存在的可靠性诊断预测方法主要有模糊评价法［1-2］，神经网络法［3］等。

模糊评价法虽然能进行模糊表达，但是其权重因子的确定存在一定的经验性，影响客观结果。神经网络法是建立模拟的多网络形式，有一定的自学、容错能力，但却受鲁棒性、收敛速度等影响，也不能很好地表现模糊性。笔者提出了一种马尔科夫模型［4］，对齿轮传动的历史数据分析，通过数学方法对齿轮失效这一动态过程进行预测［5］，既能表达过程中的模糊性又整合了经验性，预测的结果更精确。实例计算结果表明，马尔科夫模型能够准确的对齿轮传动可靠性进行预测。

2 齿轮传动可靠性预测的马尔科夫模型建立

2.1 齿轮的可靠性状态的等级划分

齿轮传动可靠性的降低，直接关系到人民财产，安全。因此对齿轮传动可靠性的等级划分应以是否满足国家标准和行业标准为准则，对机构的安全性，耐久性，适用性方面进行科学的评价。在以上准则的基础上，可以将齿轮传动可靠性分为4个等级［6］。

A级:可靠性符合国家或者行业标准，可以正常使用，可靠性高，建议机器使用这样的机构完成组装，理想状态，基本不用采取措施的齿轮传动机构。

B级:可靠性略低于国家或者行业标准，但不影响正常使用，可靠性有一定的保证，某些情况下可以使用这类机构，个别齿轮构件宜采取一定措施的齿轮传动机构。

C级:可靠性不符合国家或者行业标准，影响正常使用，可靠性存在问题，有些齿轮构件应采取措施的齿轮传动机构。

D级:可靠性严重不符合国家或者行业标准，已经不能正常使用，没有可靠性保证，且要立即采取措施的齿轮传动机构。

在确定了机构劣化状态空间S={A，B，C，D}后，为评定在某时刻的状态等级，还需确定评价指标体系和准则。对于能够量化的指标(机构变形范围等)，一般以具体数值为界线来划分等级;而对于很难量化的指标(如工作精度要求等)，评价指标的等级划分只能借助于对指标性状的定性描述。

2.2 转移概率矩阵计算

由马尔科夫原理［7-9］可知，对于Markov链{Xt，t≥0}{x(t)，t＞0}，描述其进程最基本的量就是它的转移概率Pij。设系统的状态有n个，系统在tm时间处于状态i的条件下，在下一时间tm+1转为状态j的概率为Pij，将一步转移概率Pij依序排列，即构成了一步转移概率矩阵P=(Pij)n×n。通常将其排成一矩阵形式，记为:

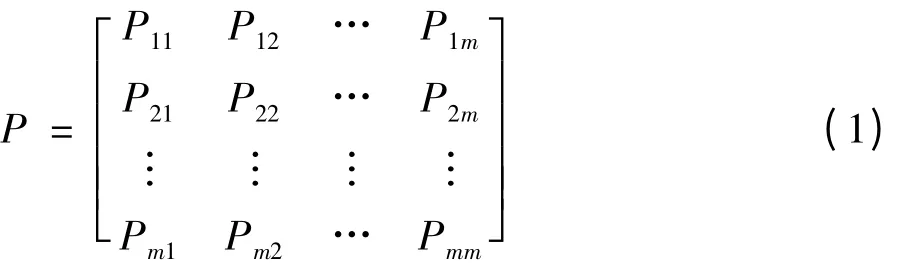
式中:Pij为从状态i转为状态j的状态转移概率。

如果已知t时刻的状态的分布Xt，则可推知(t+k)时刻的分布为:

对于齐次Markov链的转移概率矩阵P与时间t无关，在系统状态转移过程中P为一定值，因此系统在任意时刻t所处状态可由其初始状X0及其转移概率矩阵P完全确定。即t的状态分布为:t

齿轮传动的可靠性状态分4个等级，故状态转移概率矩阵为:

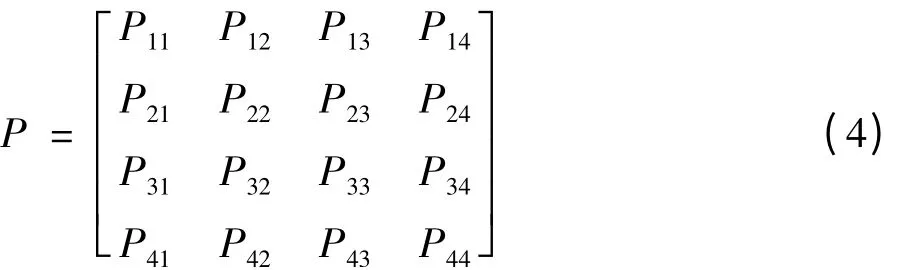
式中:Pij从状态i转为状态j的状态转移概率。若要求得转移矩阵P，则需要连续多年的数据，这样对数据的要求性很高，在实际过程中获得这样的连续数据有一定的难度。为此，考虑对状态转移矩阵进行一定的简化。当正常运行时，如忽略维修维护等措施对情况的改善，则运转过程便可以认为是一个连续均匀的过程。假定齿轮构件在某时刻的劣化状态只有2种过程:一是维持现状，二是向下一状态转移，如每次状态转移概率为Px，则保持现状的概率就为(1-Px)，其过程和状态间转移的概率如图1所示。

图1 各状态转移概率示意图

由此可以把转移概率矩阵简化为:

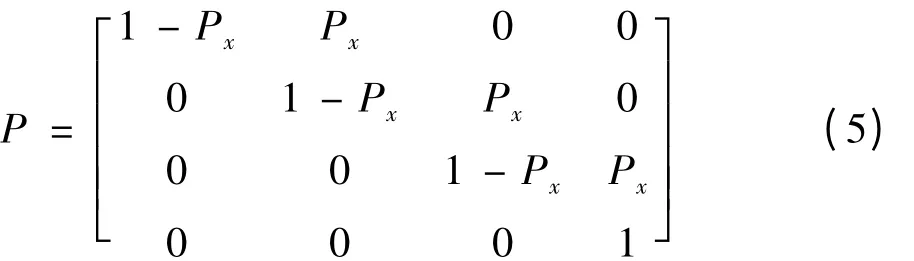
式中:Px为一种状态到下一状态的转移概率。如传动机构的初始状态为的A状态，即为X0=(1，0，0，0)T，如知运行过程中t年的状态分布为Xt=(xt1，xt2，xt3，xt4)T，则就可代入公式(6)进行运算:

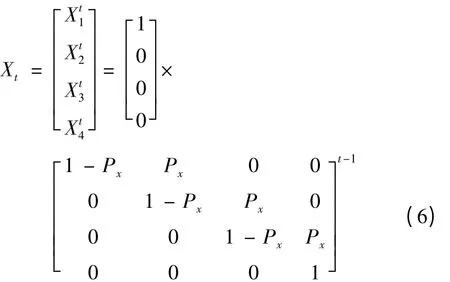
从而得到未知向量Px来确定状态转移概率矩阵P。

2.3 Markov 预测齿轮传动可靠性的实现

计算得到状态转移矩阵P后，假定选择2006年作为初始状态X0=(0，1，0，0)，即初始状态为B级，利用式(3)便可对机构寿命周期内的任一年份齿轮传动可靠性进行预测，预测结果为:

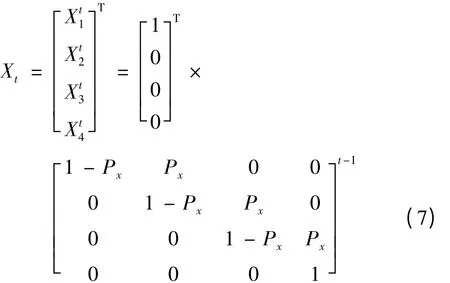
式中:Xt为齿轮传动可靠性状态等级的分布向量。

3 实例论证

由以上的叙述可知，通过马尔科夫模型可以对任何一年的齿轮机构可靠性进行预测，下面通过中国科学技术大学工程科学学院机械设计基础实验室的某10构件齿轮减速箱的可靠性状态进行数据推算验证可行性。

根据实验室的记录，该齿轮减速箱是2000年出厂，排除人为因素造成的损害，可得到齿轮减速箱齿轮各年份使用的等级状态，本文取10年的数据如表1所列。

由表1所列的数据统计分析可得初始评定向量为(0.8，0.2，0，0)。而利用模糊综合评定法得到评定向量为(0.8，0.05，0.15，0)。

表1 齿轮减速箱各年齿轮状态等级数据(个)表

综合上述结果［10］，选初始评定向量为(0.8，0.1，0.1，0)。代入式(6)计算得式(9):

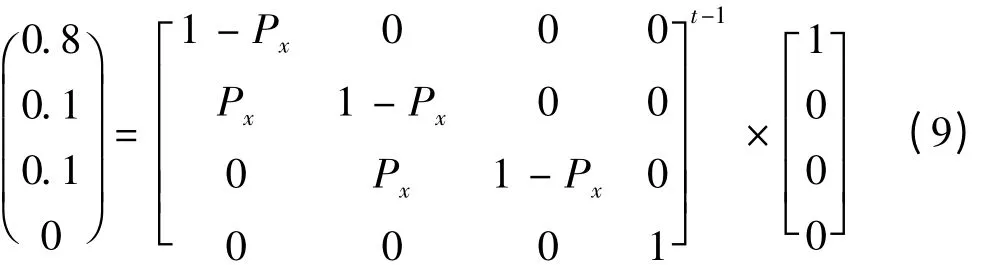
按最小二乘法原则确定得到Px的值为0.106，利用式(7)可以计算得到齿轮减速箱在任何一年的可靠性状态分布向量。

应用上面计算得到的简化状态转移矩阵，代入式(7)计算可到各年的预测结果，并通过与实际数据的对比，得到预测的准确性如表2所列。

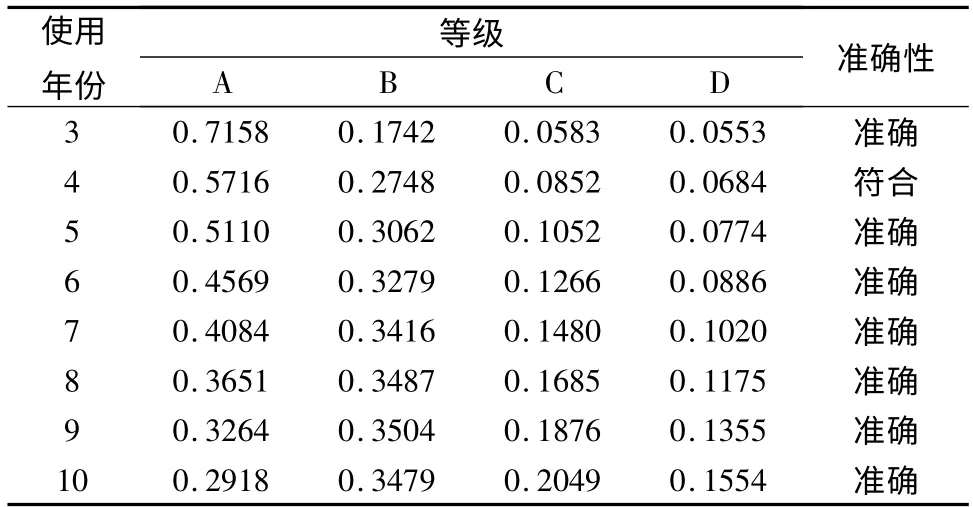
表2 基于马尔科夫模型的齿轮减速箱可靠性预测概率

由以上的预测数据和实际检测数据的对比，可以看出，预测的结果与实际状态过程基本相符，没有出现不对的情况，验证了马尔科夫模型预测的可行性，准确性。

4 结语

齿轮传动可靠性预测对保障机构的正常工作有重大的意义，能够让人们防患于未然，减少不必要的损失。本文则是在数据的统计分析和模糊评定的基础上，运用马尔科夫模型进行预测，既有统计经验又有模糊性的体现，适用性较强。通过对齿轮减速箱的可靠性预测验证了该方法的准确性，为机构的可靠性预测提供了一种新方法。而且在类似的预测中马尔科夫模型也有一定的可行性。

［1］ You Shihong，Cheng Haozhong，Xie Hong，et.Application of combination forecasting by fuzzy method in mid-and long-term load forecasting)［J］.Proceedings of the CSU—EPSA)，2004，16(3):53-56，78.

［2］ 谢季坚，刘承平.模糊数学方法及其应用［M］.第三版.武汉:华中理工大学出版社，2006.

［3］ 时建峰，时 军，时 伟，等.基于小波包与改进BP神经网络的齿轮故障诊断［J］.机械研究与应用，2011(1):82-84，87.

［4］ 戴宇文，韩大建.桥梁管理系统中的桥梁退化模型实现［J］.水运工程，2005(9):78-82.

［5］ 刘嘉馄.应用随机过程［M］.北京:科学出版社，2000.

［6］ 张启云，马 骅，郄志红.基于模糊马尔科夫的钢筋混泥土桥梁劣化预测［J］.公路交通技术，2009(4):84-86.

［7］ 何 鑫，宋平岗，官二勇.用马氏链方法预测全国年发电量趋势［J］.华东交通大学学报，2006，23(4):51-54.

［8］ Wu Kai，Lin Zhenghui.Application of Markov chain in VLSI power estimation［J］.Computer Engineering，2003，29(13):162-164.

［9］ 李 敏，江 辉，黄银华，等.马尔科夫链在电力负荷组合预测中的应用［J］.电力系统及其自动化学报，2011，23(2):131-134.

［10］ 张尧庭，方开泰.多元统计分析［M］.北京:科学出版社，1982.