基于因子分析法构建世界优秀女子沙滩排球运动员运动成绩回归模型

张晓丹，黄艳丽，谷丽颖

基于因子分析法构建世界优秀女子沙滩排球运动员运动成绩回归模型

张晓丹1，黄艳丽2，谷丽颖3

目的：探讨世界女子沙滩排球运动员基本情况、运动技术与综合实力（因子得分）之间的关系；构建综合实力（因子得分）与运动成绩间最优模型。方法：以2012年伦敦奥运会女子沙滩排球项目所有参赛的24对（共计48名）运动员为研究对象，采用因子分析法探讨运动员基本情况、运动技术与综合实力（因子得分）之间的关系，采用回归法构建综合实力（因子得分）与运动成绩间最优模型。结果：（1）基本技术因子、主动得分因子、基本条件因子和体型因子分别占世界女子沙滩排球运动员基本情况、运动技术构成比例的49.9%，13.8%，12.7%和11.3%。（2）对三个回归模型和模型偏回归系数进行检验，发现因子得分3和因子得分4不能被引入模型。结论：（1）世界女子沙滩排球运动员基本情况、运动技术构成主要体现在基本技术因子和主动得分因子。（2）综合实力（因子得分）与运动成绩间的最优回归模型应以因子得分1和因子得分2为自变量，奥运名次为因变量来构建的多元线性回归方程。

因子分析法；回归建模；沙滩排球；世界优秀女子运动员；运动成绩

沙滩排球是唯一在沙地进行的奥运会集体项目。它不仅要求运动员技术全面，而且要有充沛的体力和灵活的头脑，同时场上两名队员的配合，风、阳光等自然条件也考验运动员能否取得好的运动成绩。

我国沙滩排球运动于1994年被正式列为比赛项目，在近几年的发展中取得了较大的进步，特别是我国女队，曾创造2008年奥运会第2名，2012年伦敦奥运会第四名的好成绩，但依然距离以美国、巴西为首的世界强队有明显差距。

在评价运动成绩方法中，常见的有相关分析法[1-9]（包括灰色关联度分析），聚类分析法[10-15]、因子分析法[12,16]和回归分析法[13-14,16]等，这些方法多见于田径运动研究[1-7,10,13-14,16]，在武术[8]、蹦床[9]、羽毛球[13]、拳击[15]等项目中也有少量研究，但很少对构建的模型进行检验，且研究对象甚少涉及包括奥运会选手在内的世界高水平运动员。

目前国内外未见将以上统计方法应用于沙滩排球成绩预测。本研究拟采用因子分析法探讨世界女子沙滩排球运动员基本情况、运动技术与综合实力（因子得分）之间的关系，并根据向后迭代回归法构建综合实力（因子得分）与运动成绩间最优模型，旨在为我国女子沙滩排球运动成绩的提高提供参考。

1 研究对象与方法

1.1 研究对象

以2012年伦敦奥运会女子沙滩排球项目所有参赛的24对（共计48名）运动员的基本情况、运动技术为研究对象。其中，运动员基本情况涉及的4项指标主要依据于国际排联公布的数据[17]，包括身高、体重、年龄和根据公式BMI=体重（kg）/身高2（m2）计算出的BMI值。运动技术参照国际排联有关统计数据[18]，包括发球次数、发球直接得分数、发球得分率、进攻次数、进攻成功数、进攻成功率、拦网成功次数、防守次数、防守成功数及防守成功率共计8项指标。综合实力（因子得分）根据因子分析法得到。

1.2 研究方法

1.2.1 因子分析法 运用SPSS17.0，采用因子分析法探讨

2012年伦敦奥运会全部参赛的24对女子沙滩排球运动员基本情况、运动技术与综合实力（因子得分）之间的关系。需要说明的是，由于沙滩排球运动属于集体项目，因此，本研究中运动员基本情况、运动技术有关数据是在国际排联公布的数据基础之上，以各队为单位，取两名运动员数据的平均值。

为了使分类集中，对因子载荷矩阵采用了方差极大法进行正交旋转，根据特征值λi＞1、累计贡献率大于80%，得出反映女子沙滩排球运动员基本情况和运动技术的几个主因子，并对每个主因子进行命名。

1.2.2 回归分析法 采用向后迭代检验剔除相应变量，得到以综合实力（因子得分）预测运动成绩的最优模型。

1.2.3 文献资料法 通过查阅有关文献资料、网站，收集有关数据，作为分析研究的依据。

2 研究结果与分析

2.1 KMO和Bartlett球形检验

表1 KMO和Bartlett球形检验Table 1 KMO and Bartlett's Test

因本研究主要方法之一为因子分析法，故首先需要确定本研究是否适合采用因子分析法。一般KMO统计量大于0.9时效果为最佳，0.7以上可以接受，0.5以下不宜进行因子分析[19]，本研究中KMO取值为0.707（表1），说明本研究可以采用因子分析法进行探讨。Bartlett球形检验统计量的Sig＜0.01，由此否定相关矩阵为单位矩阵的零假设，即认为各变量之间存在显著的相关性，进而说明了有进行因子分析的必要。

2.2 世界优秀女子沙滩排球运动员基本情况、运动技术因子构成分析——运动成绩预测模型自变量的筛选

对世界优秀女子沙滩排球运动员基本情况、运动技术因子构成进行分析的过程，也是筛选运动成绩预测模型自变量的过程。

采用方差极大法进行正交旋转，根据特征值λi＞1、累计贡献率大于80%，得出反映女子沙滩排球运动员基本情况和运动技术的四个主因子（表2）。

表2中第1因子包含沙滩排球的各种基本技术，因此命名为基本技术因子。第2因子体现主动得分能力，因此命名为主动得分因子。第3、第4因子各包含两个指标，分别命名为基本条件因子和体型因子。

从表2可看出，基本技术因子和主动得分因子是决定世界优秀女子沙滩排球运动员基本情况和运动技术的主要因素，两者之和占据总体的63.7%。沙滩排球对个人技术的灵活运用要求全面[20-26]，尤其要求有突出的防守能力[27]，同时要求主动得分能力也要强[28]。

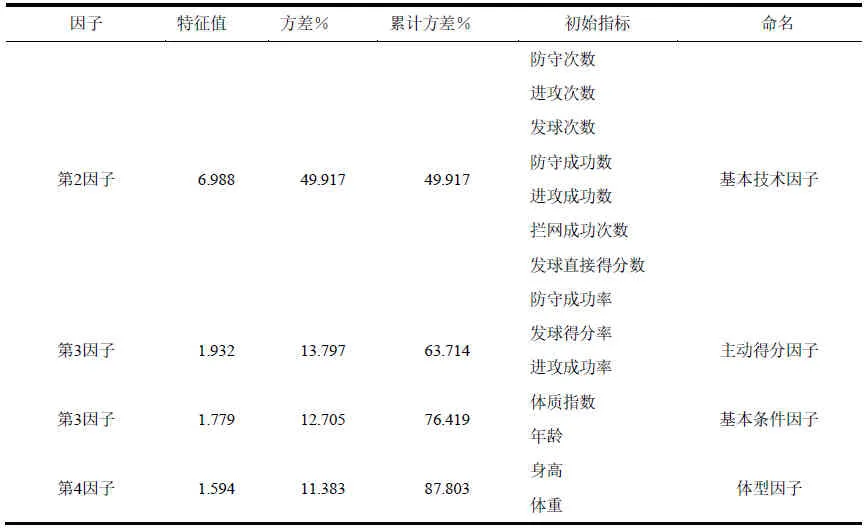
表2 旋转后各因子的特征值、总体方差解释、初始指标和命名

表2还显示，基本条件因子（体质指数、年龄）和体型因子（身高、体重）对运动成绩的影响较小，二者分别占总体的12.7%和11.4%，这与张晓丹[29]等人有关的有关研究结果一致：在2005年世界沙滩排球巡回赛上海金山站比赛中，平均身高180cm、平均体重68kg、平均年龄24岁的中国优秀女子沙滩排球组合田佳/王菲输给年长10岁、平均身高172.5cm、平均体重61.5kg的巴西老将组合Adriana/Shelda。虽然年龄及沙滩排球训练年限是影响沙滩排球运动水平的重要因素[30]，但相比较而言，基本技术和主动得分能力更为重要。本研究所得的四个因子及因子特征值从统计学角度证实了影响沙滩排球运动成绩诸多要素的重要程度。

本研究不仅需要了解世界优秀女子沙滩排球运动员运动成绩预测模型由哪几个因子构成，还需要了解每个构成因子的得分，即原始变量的标准化值和因子得分系数的乘积之和。根据因子分析法，得到四个因子的得分系数矩阵（表3），则可求出四个因子得分分别为：

FAC2_1 = -0.036*身高-0.024*体重+0.007*体质指数+…+0.04*防守成功率；

FAC2_1 = 0.001*身高+0.094*体重+0.107*体质指数+…-0.127*防守成功率；

FAC3_1 = -0.201*身高+0.24*体重+0.455*体质指数+…-0.292*防守成功率；

FAC4_1 = 0.578*身高+0.514*体重+0.073*体质指数+…+0.147*防守成功率。

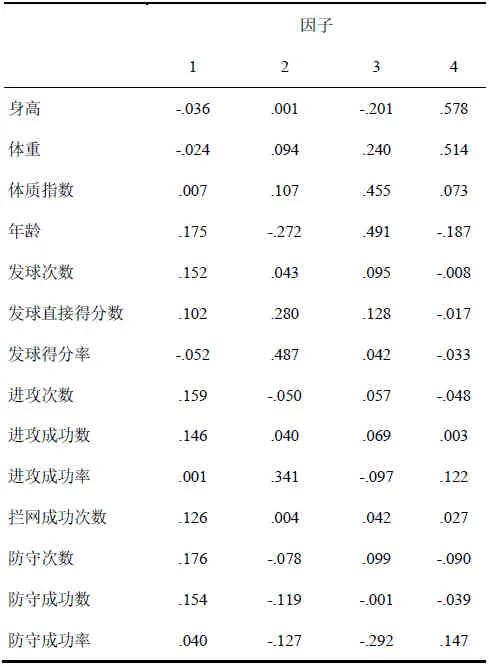
表3 因子得分系数矩阵

2.3 世界优秀女子沙滩排球运动员运动成绩预测最优回归模型的构建

本研究拟通过运动员因子得分（综合实力）预测运动成绩，故以奥运名次为因变量，四个因子得分为自变量构建回归方程，得到三个模型（表4）。

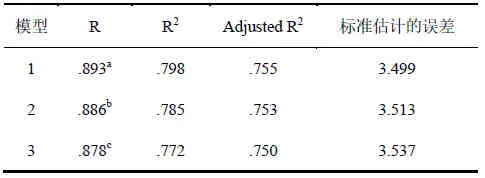
表4 模型摘要

对三个回归模型进行假设检验，结果显示三个模型都经过F检验，证明自变量和因变量之间存在线性关系[31]（表5）。对三个模型的偏回归系数进行T检验，发现三个模型中因子得分1、因子得分2的偏回归系数概率P值（Sig.）分别为＜0.001和0.069，按a=0.10水平，均具有统计学意义。而模型中因子得分3、因子得分4的偏回归系数P值均大于0.1，需进一步筛选（表6）。通过向后迭代回归法，我们发现模型2和模型3中偏回归系数假设检验的概率P值（Sig.）均大于0.05（表7），说明因子得分4和因子得分3不能被引入模型，应被剔除。

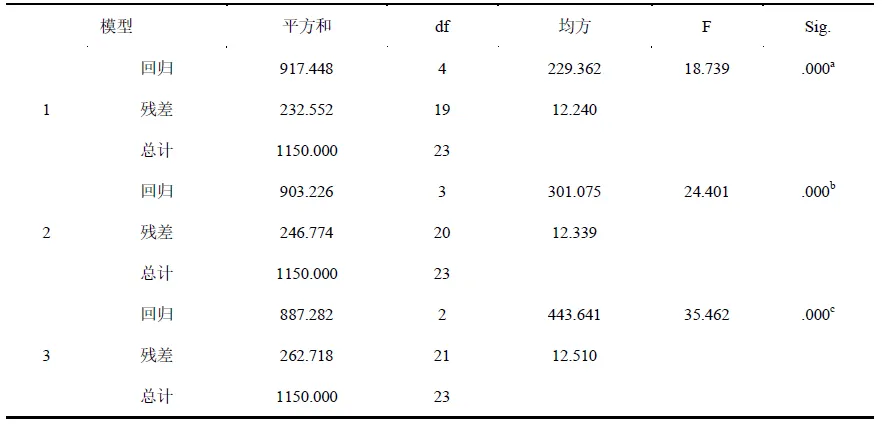
表5 方差分析

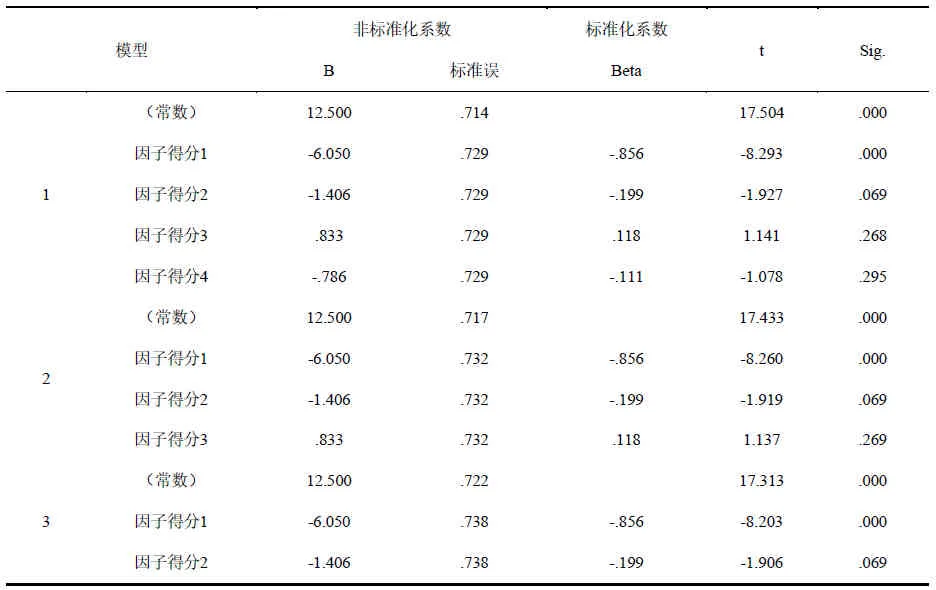
表6 系数

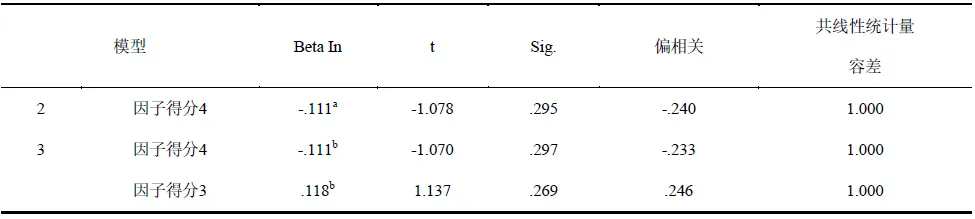
表7 已排除的变量信息统计表

综上所述，本研究运动成绩最优回归模型应以因子得分1和因子得分2为自变量，奥运名次为因变量来构建，即 Y=12.5-6.05X1-1.406X2。其中X1为因子得分1（FAC1_1），X2为因子得分2（FAC2_1），模型中的常数与偏回归系数来自表6中的常数及各指标对应的非标准化系数B。需要说明的是，由于所得模型有两个自变量，所以该回归模型显示为三维立体图（图1）。

2.4 世界优秀女子沙滩排球运动员运动成绩最优回归模型的检验

对构建的世界优秀女子沙滩排球运动员运动成绩最优回归模型及模型偏回归系数进行检验，F检验（表5）和显著性T检验结果（表6）均显示，P＜0.001，证明该模型是本研究所得的最优模型。

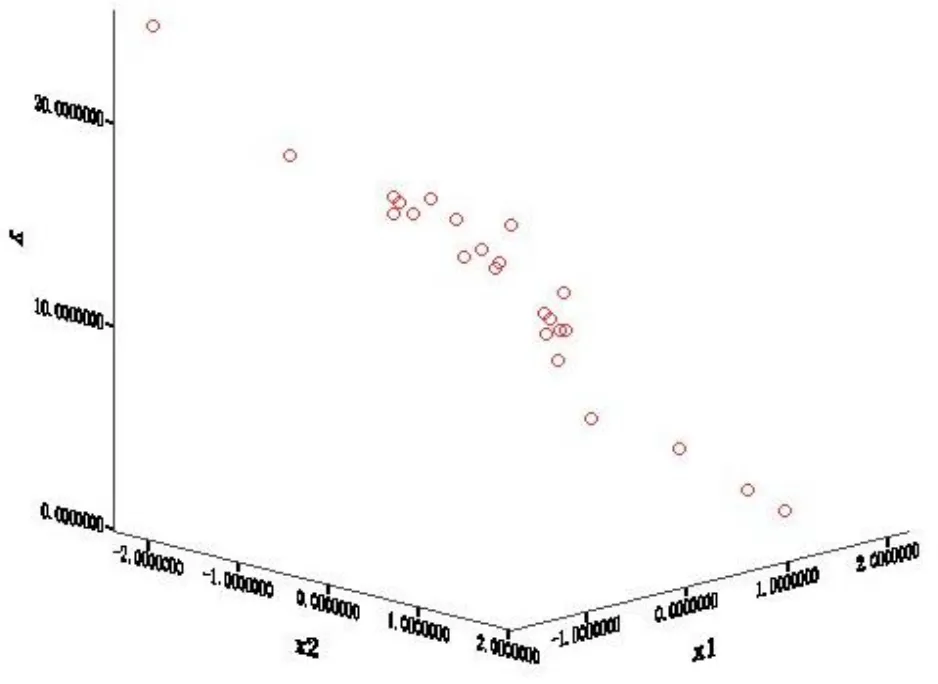
图1 二元线性方程三维示意图

由于本研究所得模型有两个自变量，故分别对两个自变量的偏回归系数显著性T检验结果进行图示（图2，图3）。图2和图3均仅有1个预测点未落入95%预测区间，证明预测效果较理想。

3 结 论

（1）世界女子沙滩排球运动员基本情况、运动技术构成主要体现在基本技术因子和主动得分因子。

（2）综合实力（因子得分）与运动成绩间的最优回归模型应以因子得分1和因子得分2为自变量，奥运名次为因变量来构建的多元线性回归方程。

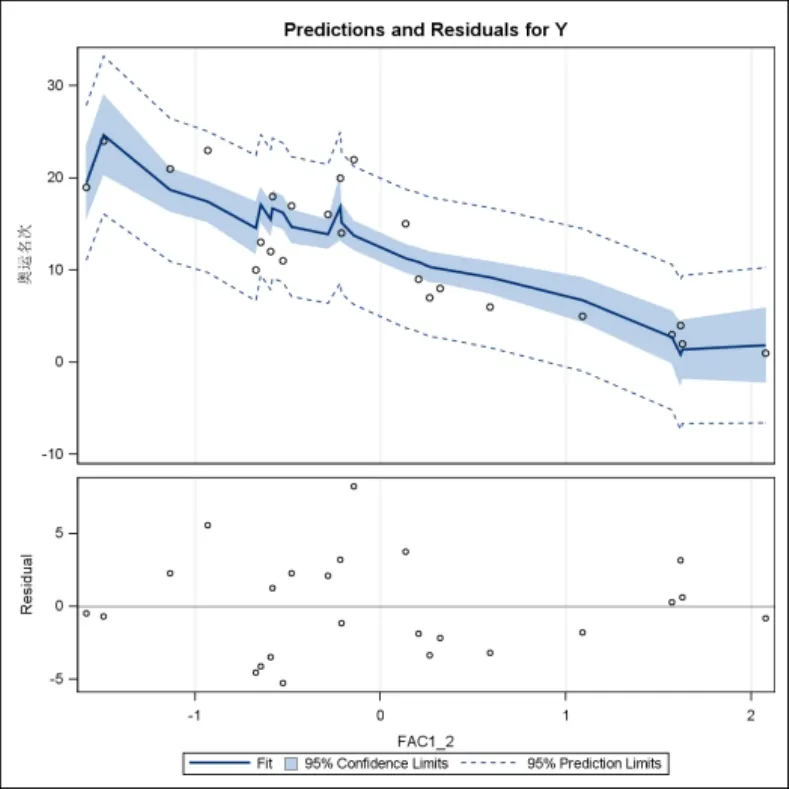
图2 因子得分1对运动成绩的模型预测图

注：上部分中的各点代表原始数据，曲线代表预测模型，阴影代表95%置信区间，虚线代表95%预测区间。下半部分代表的是残差图。若残差图呈随机散落，且绝大部分落在±2σ范围（±σ为68%的点落在预测范围，±2σ为96%的点落在预测范围），说明模型预测效果较好[32]。

图3 因子得分2对运动成绩的模型预测图

[1] 范文杰，周爱国，刘建敏. 对第28届奥运会田径运动成绩的灰色预测[J]. 北京体育大学学报，2002；25（6）：847～848.

[2] 马丽亚，许世岩，于红娟. 世界优秀男子跳高运动员起跳技术与运动成绩的灰色关联分析[J]. 首都体育学院学报，2008；20（3）：122～124.

[3] 陈发平，叶风玲. 世界优秀男子跳高运动员的各项身体素质指标与其运动成绩间的灰关联度分析[J]. 广州体育学院学报，2003；23（3）：57～60.

[4] 杜和平. 男子100m短跑运动员身体素质与运动成绩的灰色关联度研究[J]. 广州体育学院学报，2006；26（5）：85～87.

[5] 朱 泳. 不同水平男子百米运动员的身体素质与运动成绩的灰色关联度分析[J]. 广州体育学院学报，2004；24（4）：57～60.

[6] 车晓波. 对于娟运动成绩的灰色关联度分析[J]. 上海体育学院学报，1996，20（2）：49～52.

[7] 任占兵. 中跑运动员跑步经济性与运动成绩的相关性分析[J].中国体育科技，2011，47（2）：26～30.

[8] 刘福君. 影响武术运动成绩诸因素的层次分析[J]. 武汉体育学院学报，2000，34（5）：76～78.

[9] 吴家舵，戴金彪，杨 烨，等. 我国优秀青少年羽毛球运动员心理特征与运动成绩的相关研究[J]. 上海体育学院学报，2000，24（4）：58～61.

[10] 焦建军，康利则. 影响我国女子铅球运动员运动成绩的主要身体素质及评价标准的研究[J]. 中国体育科技，2005；41（3）：47～52.

[11] 茅 洁，梅 焰. 灰色ART聚类分析法在竞技体育生化指标监控中的应用[J]. 武汉体育学院学报，2005；39（10）：51～52.

[12] 司友志，吴成林. 基于主成分分析、因子分析与聚类分析运动员的运动能力评价方法研究[J]. 四川体育科学，2009（3）：146～150.

[13] 徐勤儿，王家宏. 中外优秀女子200m跑运动员速度分配多元分析[J]. 山东体育学院学报，2007；23（3）：89～91.

[14] 孙有平，曲淑华，罗达勇，等. 影响我国优秀男子铁饼运动员运动成绩的主要因素分析[J]. 北京体育大学学报，2001；24（3）：391～392，421.

[15] 张 莉，马维民. 青少年优秀拳击运动员身体成分生理机能相对指标特征与聚类分析[J]. 体育学刊，2006，31（1）：68～71.

[16] 魏春玲. 我国十项全能运动成绩的因子分析及灰色系统回归预测研究[J]. 体育科学，2004；24（11）：51～53.

[17] Players' Database[EB]. http：//www.fivb.org/ EN/BeachVolleyball/PlayersDatabase.asp.

[18] Team Ranking by Skill[EB]. http：//www.fivb.org/en/olympics/ london2012/PDF/B6-WLON2012.pdf.

[19] 杜 强，贾丽艳. SPSS统计分析从入门到精通[M]. 北京：人民邮电出版社，2011.

[20] 张晓丹. 中国优秀女子沙滩排球运动员体能特征及其评价体系研究[D]. 北京体育大学，2007.

[21] 陈少坚，庄小平. 沙地与室内排球若干技术效果比较研究[J].西安体育学院学报，1999；16（2）：40～41.

[22] 王吉生. 高水平女子沙滩排球比赛攻防技术运用效果的研究[D]. 北京体育大学，2002.

[23] 徐伯彤. 沙滩排球新规则对技战术影响与导向[J]. 广州体育学院学报，2003（3）：68～70.

[24] 韩 波，王 舒. 沙滩排球技术探讨[J]. 南京体育学院学报（自然科学版），2007（3）：72～73.

[25] 傅渔庭，陈桂红. 沙滩排球基本技术浅探[J]. 南京体育学院学报，1999（3）：13.

[26] 姜 虹. 沙滩排球的技、战术特点及训练对策[J]. 沈阳体育学院学报，1995（4）：18～20.

[27] George Giatsis, Maria Tili, Eleni Zetou. The height of the women‘s winners FIVB Beach Volleyball in relation to specialization and court dimensions[J]. VOLUME，2011，（6）：497～503.

[28] JM Cortell-Tormo, JA Perez-Turpi, JJ Chinchilla, et al. Analysis of movement patterns by elite male players of beach volleyball[J], Perceptual and Motor Skills，2011，112（1）：21～28.

[29] 张晓丹，赵凤萍，曹庆雷，等. 实际比赛中田佳/王菲与Adriana Behar/ Shelda的体能分配特征比较[J]. 天津体育学院学报，2005；20（5）：93～95.

[30] 张晓丹，葛春林，王卫星. 中国优秀女子沙滩排球运动员身体形态特征[J]. 中国体育科技，2009；45（1）：64～68.

[31] 李 竹，郑俊池. 新编实用医学统计方法与技能[M]. 中国医药科技出版社，北京：1998.

[32] 卢纹岱. SPSS for Windows统计分析[M]. 电子工业大学. 北京：2000.

Construction of Sport Performance Regression Model for World-class Elite Female Beach Volleyball Players Based on the Factor Analysis Method

ZHANG Xiao-dan1，HUANG Yan-li2，GU Li-ying3

Objective: To investigate the relationships between basic condition, Sport technique, And comprehensive capability （component score） of world-class female beach volleyball players and to construct the optimal model between comprehensive capability （component score） and sport performance. Methods: Taking the examples of 24 pairs （totally 48 players） of female beach volleyball players of the 2012 London Olympic Games and by using the factor analysis method, this paper discussed the relationships between basic condition, sport technique, And comprehensive capability. And by regression model, this paper tried to construct the optimal model between comprehensive capability （component score） and sport performance. Results: （1） Basic technical factor, initiative score factor, basic condition factor and somatotype factor respectively accounted for 49.9%, 13.8%, 12.7 and 11.3% of the component proportion of the basic condition and sport technique of the world-class female beach volleyball players. （2） The three regression models constructed and model partial regression coefficients were tested and it was confirmed the component score 3 and component score 4 cannot be introduced into models. Conclusions: （1） The component of basic condition and sport technique of the world-class female beach volleyball players mainly embodied in the basic technical factor and the initiative score factor. （2） The optimal regression model between the comprehensive capability （component score） and sport performancewas a multiple linear regression equation which should take component score 1 and component score 2 as independent variables, and take the Olympic ranks as dependent variable.

Factor analysis method; Regression model; Beach volleyball; World-class elite female players; Sport performance

G842

A

1007―6891（2013）06―0059―07

2013-04-15

国家体育总局科研项目，编号：07116。

1.天津市体质检测中心，天津体育学院，天津，300381；2.天津体育学院研究生部，天津，300381; 3.天津体育学院体育文化传媒系，天津，300381。1.Tianjin Municipality Physical Fitness Surveillance Center, Tianjin University of Sport, Tianjin, 300381,China; 2.School of Gratuate, Tianjin University of Sport, Tianjin, 300381,China; 3. Department of Sports Culture and Media, Tianjin University of Sport, Tianjin,300381,China.