基于双线性算子计算薛定谔方程组的精确解
2013-06-27赵敬宜李壹宏
赵敬宜,李壹宏
(1.西北大学数学系,陕西西安 710127;2.西北大学非线性研究中心,陕西西安 710069)
基于双线性算子计算薛定谔方程组的精确解
赵敬宜1,2,李壹宏1,2
(1.西北大学数学系,陕西西安 710127;2.西北大学非线性研究中心,陕西西安 710069)
通过引进双线性算子,用合适的变换将已知方程组转化为双线性方程,并用扰动法求得方程组的单孤子和双孤子解.其结果有助于对数学方程的理解和在物理中的应用.
双线性算子;薛定谔方程组;孤子解
DO I:10.3969/j.issn.1008-5513.2013.04.008
1 引言
在广泛的流体力学问题中都会遇到Davey-Stewartson方程组(简称为DS方程组).其形式可写为[1]:
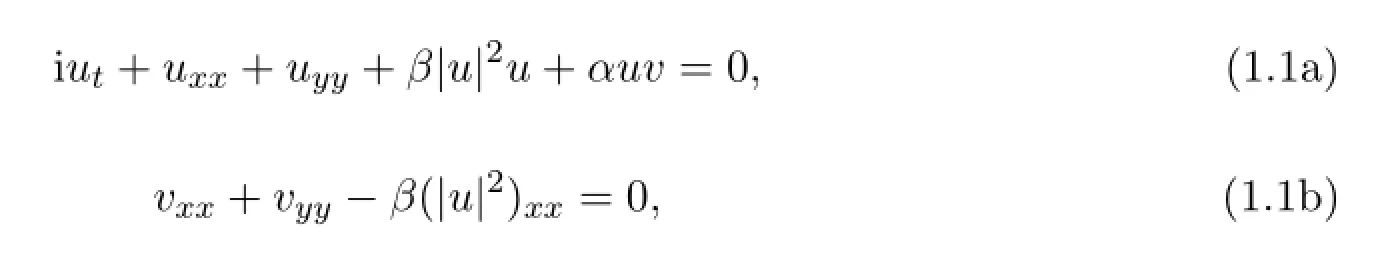
其中u(x,y,t)为复函数,v(x,y,t)为实函数,γ,β为非线性系数,α为相互作用系数.而随着非线性数学物理方程的广泛应用,对于求此类方程的解已有许多方法[2-4],如逆反射法、Painlev´e展开法、B¨acklund变换法、Jacobian椭圆函数法等等,此方程也可看作是1+1维非线性薛定谔方程即NLS方程向2+1维的拓广[3].本文主要应用Hirota双线性法[5]求NLS方程组的精确孤子解,其形式为[6]:

式中β,γ,δ为任意实常数.
2 求解非线性方程组的H irota直接法

3 N LS方程组的单孤子解

4 N LS方程组的双孤子解


[1]Davey A,Stewartson K.On three-dimensional packets of surfacewaves[J].Proceedings of the Royal Society of London.A.M athem atical and Physical Sciences,1974,338(1613):101-110.
[2]刘式适,刘式达.物理学中的非线性问题[M].北京:北京大学出版社,2000.
[3]李翊神.孤立子可积系统[M].上海:上海科技教育出版社,1999.
[4]A rkadiev V A,Pogrebkov A K,Polivanov M C.Inverse scattering transform m ethod and soliton solutions for Davey-Stewartson II equation[J].Physica D:Non linear Phenom ena,1989,36(1):189-197.
[5]Hirota R.The Direct M ethod in Soliton Theory[M].Cambridge:Cambridge University Press,2004.
[6]钱贤民,张叶.双线性算子和非线性方程的双线性形式[J].绍兴文理学院学报:自然科学版,2002,22(10):10-15. [7]高斌,刘式达,刘式适.Davey-Stewartson方程组的包络周期解和孤立波解[J].物理学报,2009,58(4):2155-2158.
Exact solu tions of a coup led Sch r¨od inger equations based on
b ilinear operator
Zhao Jingyi1,2,Li Yihong1,2
(1.Department of M athematics,Northwest University,Xi′an 710127,China; 2.Center for Nonlinear Studies,Northwest University,Xi′an 710069,China)
The non linear Schr¨odinger equation is transformed and expressed by using bilinear operator,and the soliton solutions are obtained through the perturbation method.M eanwhile,the result helps us to learn more aboutmathematics equation and the equation applied in physics.
bilinear operator,a coup led Sch r¨od inger equations,soliton solution
O 175.2
A
1008-5513(2013)04-0382-05
2012-12-18.
赵敬宜(1989-),硕士生,研究方向:非线性偏微分方程.
2010 M SC:35J15
