局部θ-连通空间的几个性质
2013-06-27汪贤华
汪贤华
(北京石油化工学院数理系,北京 102617)
局部θ-连通空间的几个性质
汪贤华
(北京石油化工学院数理系,北京 102617)
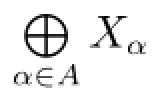
拓扑空间;连通空间;θ-连通空间;局部θ-连通空间;θ-连通分支
DO I:10.3969/j.issn.1008-5513.2013.04.005
1 引言
连通空间是拓扑空间中一类非常重要的拓扑空间[1],它是用分离集来定义的,即拓扑空间X称为连通的是指如果X不能表示为两个非空的分离子集的并集.对连通空间的研究是一般拓扑学研究的一个重要课题,文献[2]研究了δ-连通空间.文献[3]研究了θ-连通空间及其相关的一些性质,随后文献[4-5]对局部θ-连通空间和弱θ-连通空间做了一些相关的研究,本文在此基础上进一步讨论了局部θ-连通空间的充要条件,并研究了在商映射下的不变性,最后讨论了局部θ-连通空间的可和性与可积性,从而进一步完善了θ-连通空间及θ-连通性等理论.
2 基本定义
假设(X,τ(X))是一拓扑空间,A是X的子集,C lX(A)表示A在X中的闭包.文中未给出的定义请参阅文献[1].在文献[6-7]中,关于θ-闭集的定义如下:
定义1[6-7]拓扑空间X的子集A称为X的θ-闭集是指如果对于任意的p∈XA,都存在U∈τ(X),使得

类似于闭包的定义,有下面的定义:
定义2[3]假设A是拓扑空间X的子集,称x∈X是A的θ-聚点是指如果对任意的包含x的U∈τ(X),都有

定义3[3]假设A是拓扑空间X的子集,集A的一切θ-聚点构成的集合称为A的θ-闭包,记作[A]θ.
定义4[3]拓扑空间X的子集P,Q称为θ-分离的是指

定义5[3]设X是一拓扑空间,如果X不能表示为两个非空的θ-分离子集的并集,则称X是θ-连通空间.设S是X的子集,如果S作为子空间是θ-连通的,则称S是X的θ-连通子集.
定义6[4-5]设x是拓扑空间X中的一点,如果对X中任意包含x的开集U,都存在X中的一个θ-连通的开集V,满足x∈V⊂U,则称X在x点处是局部θ-连通的.若X在每一点处都是局部θ-连通的,则称X是一个局部θ-连通空间.若拓扑空间X的子集Y作为X的子空间是局部θ-连通的,则称Y是X的局部θ-连通子集.
定义7[5]设(X,τ(X))是一拓扑空间,B是τ的一个基,若B中每一个元素都是θ-连通的,则称B为X的θ-连通基.
定义8[3]拓扑空间X的一个子集称为X的θ-连通分支是指如果它是θ-连通的,并且不是X其它θ-连通子集的真子集.
3 主要结论
在文献[3]中,得到了性质:设A是拓扑空间X的子集,如果A是连通的,则A一定是θ-连通的.也就是θ-连通空间是比连通空间更广泛的一类空间.在文献[5]中作者证明了局部连通空间是局部θ-连通空间.说明局部θ-连通空间是比局部连通空间更广泛的一类空间.
局部连通性对于开子集有遗传性,在局部θ-连通空间中,对于开子集也有:
定理1若X是局部θ-连通空间,A⊂X是X的开子集,则A是局部θ-连通空间.
证明对于A中的任意一点x,设U是A中包含x的任意开集,则由于A是X的开子集,所以U也是X的开集,x∈U,再由X是局部θ-连通空间,故存在X中的θ-连通开集W,使得:x∈W⊂U,而W⊂A,A是X的开子集,所以W亦是A中的θ-连通开集,因此A是局部θ-连通空间.
定理2局部θ-连通空间的θ-连通分支是开集.
证明设X是局部θ-连通空间,A是X的θ-连通分支.对于任意的x∈A,x有一个θ-连通邻域,它也必含在A中,所以x是A的内点,因此A是开集,即局部θ-连通空间的θ-连通分支是开集.
定理3设(X,τ(X))是一拓扑空间,则下列命题等价:
(1)X是局部θ-连通空间;
(2)X的任意开集的任意θ-连通分支都是开集;
(3)X有一个θ-连通基;
(4)对于任意的x∈X,x有一个θ-连通的邻域基B(x).
证明(1)⇒(2)⇒(3)见文献[4]定理2.
(3)⇒(4)设X有一个θ-连通基B,则对于任意x∈X,令
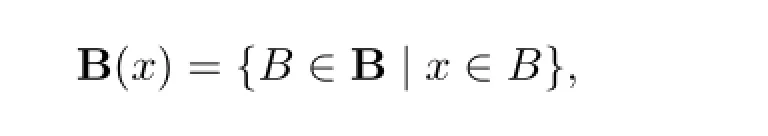
由于连通基B中每一元素都是θ-连通的,故B(x)就是x的一个θ-连通的邻域基.
(4)⇒(1)假设对于任意的x∈X,x有一个θ-连通的邻域基B(x),U是X中包含x的任意开集,则由邻域基的定义存在θ-连通开集V∈B(x),使得x∈V,令Vx≡U∩V,则Vx是θ-连通的,且x∈Vx⊂U,所以X是局部θ-连通空间.
对于局部连通空间,在商映射下是保持不变的,对于局部θ-连通空间同样也有:
定理4设f:X1→X2为商映射,若X1是局部θ-连通空间,则X2也是局部θ-连通空间.
证明设A是X2中的任意开集,B是A的θ-连通分支,由定理3知,只需证明B是开集即可.设x∈f-1(B),则x∈f-1(A)=U,由于f是商映射,故U是开集.设K是U的θ-连通分支,由于X1是局部θ-连通空间,故x∈K⊂U,K是θ-连通的开集,f(K)是θ-连通的,且f(x)∈f(K),由f(x)∈B知f(K)∩B/=∅,故f(K)∪B是A中的θ-连通子集,因此
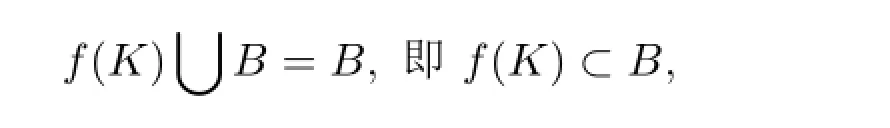
所以x∈K⊂f-1(B),也就是f-1(B)是开集,再由f是商映射,则B是开集,故X2也是局部θ-连通空间.
推论1设f:X1→X2是连续且满的开(或闭)映射,若X1是局部θ-连通空间,则X2也是局部θ-连通空间.
在文献[1]中有,局部连通空间具有可和性,对于局部θ-连通空间的可和性,同样也有下面的定理:
定理5设A是一指标集,{Xα}α∈A是一组两两不相交的拓扑空间族,则和空间
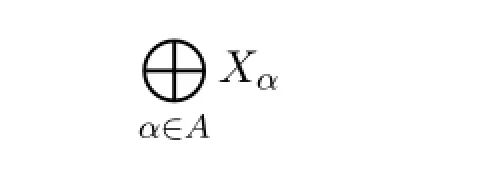
是局部θ-连通空间当且仅当对任意α∈A,Xα是局部θ-连通空间.
证明令
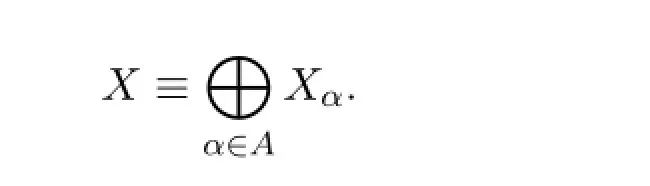
充分性设对任意α∈A,Xα是局部θ-连通空间.任给x∈X,U为X中任意包含x的开集,则存在α0∈A使得x∈Xα0,则U∩Xα0即为Xα0中的开集.而Xα0是局部θ-连通空
间,故存在Xα0中的θ-连通开集V,使得:

由Xα0是X中的开集,易知V也是X中的θ-连通开集,所以:
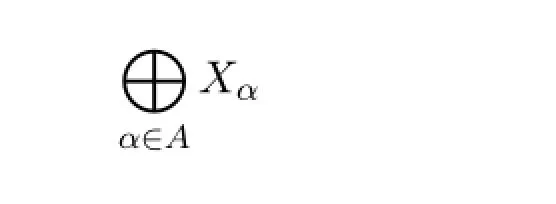
是局部θ-连通空间.
必要性设X是局部θ-连通空间.对任意α∈A,设x∈Xα,U为Xα中包含x的任意开集,则x∈X,且U亦是X中包含x的开集,由于X是局部θ-连通空间,故存在X中的θ-连通开集V,使得:x∈V⊂U,而Xα是X的既开又闭的子空间,所以V亦是Xα中的θ-连通开集.即:Xα是局部θ-连通空间.
即局部θ-连通空间也具有可和性.
对于可积性,也有类似于局部连通空间的性质:
定理6设S是一指标集,对于任意的s∈S,Xs是非空的,则乘积空间
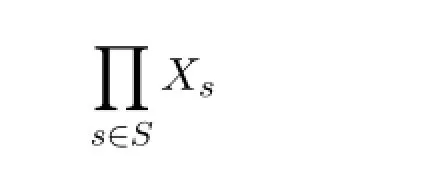
是局部θ-连通空间当且仅当对于任意的s∈S,Xs是局部θ-连通空间,且除了有限个以外还是θ-连通空间.
证明充分性假设对于任意的s∈S,Xs是局部θ-连通空间,且当s∈S{s1,s2,…,sn},Xs是θ-连通空间.当s/∈S{s1,s2,…,sn},由于Xs是局部θ-连通空间,故由定理3知Xs有一个θ-连通基Bs,令
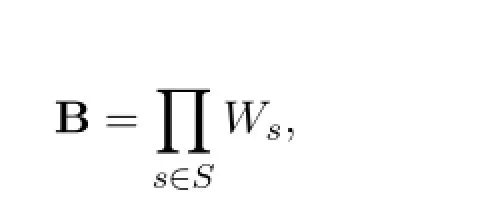
其中当s/∈S{s1,s2,…,sn}时,Ws∈Bs,当s∈S{s1,s2,…,sn}时,Ws=Xs,则B是X的一个θ-连通基,由定理3知积空间
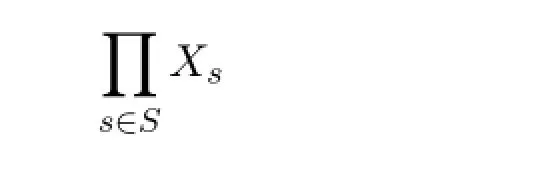
是局部θ-连通空间.
必要性假设积空间

是局部θ-连通空间,则对于任意的s∈S,ps:X→Xs是投影映射,则每个ps都是连续开映射,由推论1可得对于任意的s∈S,Xs是局部θ-连通空间.
现取任意x∈X,由X是局部θ-连通空间,设U是包含x的θ-连通开集,于是存在积拓扑中的基元素
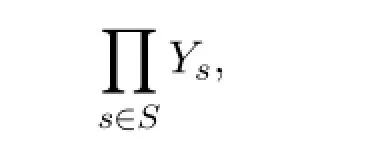
其中s∈S{s1,s2,…,sn}时,Ys=Xs,使得
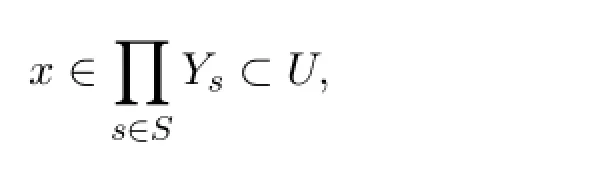
于是当s∈S{s1,s2,…,sn}时,ps(U)⊃Ys=Xs,故Xs=ps(U)是θ-连通空间.
推论2[4]若X1,X2,…,Xn都是局部θ-连通空间,则X=X1×X2×…×Xn也是局部θ-连通空间.
通过以上的研究,不难发现局部θ-连通空间与局部连通空间有着非常类似的拓扑性质,对于局部连通空间的其他一些性质,例如和紧空间有关的性质,是否也可以推广到局部θ-连通空间还有待于进一步的研究.
[1]Engelking R.General Topology[M].Warszawa:PWN,1977.
[2]汪贤华.δ-连通空间[J].纯粹数学与应用数学,2004,20(3):243-247.
[3]汪贤华,高汝林.θ-连通空间及其性质[J].北京石油化工学院学报,2005,13(1):61-64.
[4]姜金平,王小霞.局部θ-连通空间[J].江西科学,2008,26(1):11-12.
[5]姜金平,王小霞.弱θ-连通空间及其性质[J].西南民族大学学报:自然科学版,2008,34(1):36-38.
[6]D ikran jan D,G iu li E.S(n)-θ-closed spaces[J].Top.and its A pp l.,1988(28):59-74.
[7]Filippo Cammaroto,G iovanni Lo Faro,Jack Porter R.N-Sets and near com pact spaces[J].Bollettino U.M.I,1999,(8,2-B):291-298
The several p roperties of localθ-connected space
Wang Xianhua
(Department of Mathematics and Physics,Beijing Institute of Petrochem ical Technology, Beijing 102617,China)
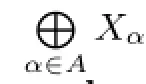
topological space,connected space,θ-connected space,localθ-connected space,θ-com ponent 2010 M SC:54D 05,54B10
O189.11
A
1008-5513(2013)04-0359-05
2013-05-09.
北京市教育委员会科技计划面上项目(Z2011-008).
汪贤华(1977-),硕士,讲师,研究方向:一般拓扑学.
