Hom-Hopf代数上的交叉积

孔翔,郑乃峰

(1.宁波工程学院理学院,浙江宁波 315211;2.宁波大学理学院,浙江宁波 315211)

Hom-Hopf代数上的交叉积

孔翔1,郑乃峰2

(1.宁波工程学院理学院,浙江宁波 315211;2.宁波大学理学院,浙江宁波 315211)

在Hom-Hopf代数上,定义了Hom-交叉积的概念.并且,得到了它的两种特殊形式:Hom-smash积和Hom-扭积.并且,给出了Hom-扭积是Hom-Hopf代数的充要条件.

Hom-Hopf代数;Hom-交叉积;Hom-扭积;Hom-模代数

1 引言

Hom-代数的概念是由Makhlouf和Silvestrov于2006年在研究拟李代数时引入的[1]. Hom-代数的引入实际上是推广了结合代数的概念,把结合代数中的结合性法则作了形变,将其变成了线性变换α结合性条件,即α(a)(bc)=(ab)α(c).随着Hom-代数研究的深入,一些学者[2-4]又陆续引入了Hom-余结合余代数、Hom-双代数和Hom-Hopf代数等,并给出了一些重要的性质.

文献[5-7]分别独立地把群交叉积的理论推广到了Hopf代数上,定义并研究了Hopf代数上的交叉积,而Boca给出了交叉积是Hopf代数的充分条件.本文的主要目的是在Hom-Hopf代数上引进交叉积的概念并研究其性质,并给出了作为交叉积的一种特殊形式的扭积是Hom-Hopf代数的充要条件.

本文的所有工作都在域k上进行的.所讨论的模、张量积和线性映射均指域k上的.文中将使用Sweedler关于余代数余乘法的记号

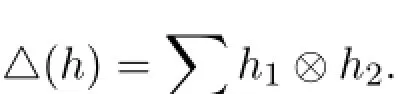
S(或SH)表示Hom-Hopf代数H的对极映射.

2 Hom-Hopf代数

3 Hom-交叉积

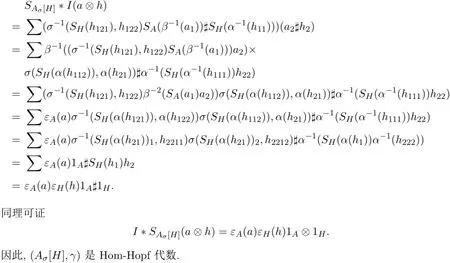
[1]Makhlouf A,Silvestrov S.Hom-algebras structures[J].J.Gen.Lie Theory Appl.,2008,2:51-64.

[2]Makhlouf A,Silvestrov S.Hom-algebras and Hom-coalgebras[J].J.Alg.Appl.,2010,9:553-589.

[3]Caenepeel S,Goyvaerts I.Monoidal Hom-Hopf algebras[J].Comm.Alg.,2011,39:2216-2240.

[4]Yau D.Hom-bialgebras and comodule Hom-algebras[J].Inter.Elect.J.Alg.,2010,8:45-64.

[5]Blattner R J,Cohen M,Montgomery S.Crossed products and inner actions of Hopf algebras[J].Trans. AMS,1986,298:671-711.

[6]Doi Y,Takeuchi M.Cleft comodule algebras of a bialgebra[J].Comm.Alg.,1986,14:801-818.

[7]Boca I.A central theorem for Hopf algebras[J].Comm.in Alg.,1997,25(8):2593-2606.

[8]Yau D.Hom-quantum groups I:quasi-triangular Hom-bialgebras[J].arXiv:0912.4128.

[9]Yau D.Hom-quantum groups III:representations and module Hom-algebras[J].arXiv:0911.5402vl.

Crossed products over Hom-Hopf algebras

Kong Xiang1,Zheng Naifeng2

(1.Faculty of Science,Ningbo University of technology,Ningbo315211,China;
2.Faculty of Science,Ningbo University,Ningbo315211,China)

In this paper,the notion of Hom-crossed products over Hom-Hopf algebras is defned and the Homsmash products and the Hom-twisted products are their special cases.Moreover,a necessary and sufcient conditions for a Hom-twisted product to be a Hom-Hopf algebra is given.

Hom-Hopf algebra,Hom-crossed product,Hom-twisted product,Hom-module algebra

O153.3

A

1008-5513(2013)06-0582-09

10.3969/j.issn.1008-5513.2013.06.006

2013-06-16.

国家自然科学基金(60873267).

孔翔(1979-),硕士,讲师,研究方向：Hopf代数及量子群等.

2010 MSC:16W30