关于Diophantine方程x2+y2n=z3的可解性

刘红艳

(西安理工大学理学院,陕西西安 710054)

关于Diophantine方程x2+y2n=z3的可解性

刘红艳

(西安理工大学理学院,陕西西安 710054)

运用有关三元Diophantine方程的新近结果,证明了一类Diophantine方程没有适合特定条件的正整数解,得到了更一般的结论,推广了相关文献的结果.

高次Diophantine方程;三元Diophantine方程;广义Fermat猜想

1 引言

设Z,N分别是全体整数和正整数的集合.众所周知,自从A.Wiles成功解决了著名的Fermat猜想之后,广义Fermat猜想已成为数论中有关Diophantine方程的重要研究课题,文献[1-5]给出了一些研究结论,该猜想可表述为:

这是一个迄今远未解决的难题,目前只证实了一些极特殊的情况.本文将讨论猜想A在r=2,2|s且t=3时的情况,此时该猜想可表述为:

对此,文献[6]证明了:当n是适合5＜n＜107以及n/=31的奇素数时,方程(1.2)无解.最近,在文献[7]中S.R.Dahmen解决了3|n,n∈{5,31}以及n是适合n≡-1(mod 6)的奇素数时的情况.本文对于一般的n证明了以下结果:

定理方程(1.2)没有满足条件n≥4以及2|y的解(x,y,z,n).

2 若干引理

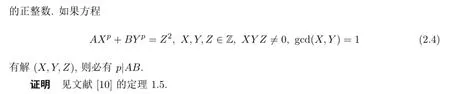
3 定理的证明

参考文献

[1]Beukers F.The diophantine equation Axp+Byq=Czr[J].Duke Math.J.,1998,91(1):61-88.

[2]Darmon H.Faltings plus epsilon,Wiles plus epsilon,and the generalized Fermat equation[J].C.R.Math. Acad.Sci.Soc.R.Canada,1997,19(1):3-14.

[3]Darmon H.A fourteenth lecture on Fermat′s Last Theorem[J].CRM Proceedings and Lecture Notes, 2004,36:103-115.

[4]Bugeaud Y,Hanrot G,Mignotte M,et al.Number theory II[M].New York:Springer,2007.

[5]盖伊.数论中未解决的问题[M].3版.北京:科学出版社,2007.

[6]Chen I.On the equation s2+y2p=α3[J].Math.Comput.,2008,77(262):1223-1227.

[7]Dahmen S R.A refned modular approach to the diophantine equation x2+y2n=z3[J].Int.J.Number Theory,2011,7(5):1303-1316.

[8]Mordell L J.Diophantine Equations[M].London:Academic Press,1969.

[9]Bruin N.The diophantine equations x2±y4=±z6and x2+y8=z3[J].Compos.Math.,1999,118(3):305-321.

[10]Bennett M A,Skinner C M.Ternary diophantine equations via Galois representations and modular forms[J]. Canada J.Math.,2004,56(1):23-54.

On the solvability of the Diophantine equation x2+y2n=z3

Liu Hongyan

(School of Scince,Xi′an University of technology,Xi′an710054,China)

Using recent results of ternary diophantine equations,we prove that the equation has no positive integer solution with certain conditions,give a general conclusion and extend the results of related literature.

higher diophantine equation,ternary diophantine equation,generalized Fermat conjecture

O156.4

A

1008-5513(2013)06-0572-05

10.3969/j.issn.1008-5513.2013.06.004

2013-09-07.

国家自然科学基金(11071194).

刘红艳(1974-),硕士,副教授,研究方向：数论及其应用.

2010 MSC:11B83