谐波补偿重复控制及其在逆变器控制中的应用

杨豪，赵军红，朱雁南，刘岳滨

（第二炮兵工程大学，陕西 西安 710025）

1 引言

在众多基于周期的控制方案中，基于内模原理［1］的重复控制对于解决谐波补偿问题是一种简单有效的方法。 传统的重复控制［2－3］（CRC）在开环系统的前向通道上嵌入周期为L0的任意周期信号的内模e-sL0(1-e-sL0)，有效实现对各次谐波分量的无差补偿，从而实现零稳态误差。然而，传统的重复控制在谐波补偿中还存在两方面不足：一方面，从重复控制器内模的数字实现形式［4－6］z-N/(1-z-N)可以看出，其输入到输出滞后了一个基波周期，响应速度较慢，且需要的内存单元数至少为N；另一方面，在很多实际应用中，需要补偿的谐波信号往往集中在某些特定频率处，例如整理性负载给单相逆变器带来的谐波成分主要是奇次谐波，给三相逆变器带来的主要是6l±1（l＝1，2，3，…）次的谐波成分。 而传统的重复控制没有选择性地对各次谐波都进行了补偿，势必导致内存浪费、补偿速度减慢，难以满足实际系统对控制性能的要求。针对上述问题，文献［7］和文献［8］分别提出了一种奇次谐波补偿重复控制器和6l±1次谐波补偿重复控制器。

文献［7－8］采用类似的谐波补偿重复控制器，是一个值得研究的课题。目前，也没有一种通用的重复控制可以将所有的重复控制统一起来。为此，本文提出一种nl±m次谐波补偿重复控制（HCRC），以增强重复控制对谐波补偿的选择性。该重复控制可以实现对nl±m次谐波的无差补偿，通过给n和m赋以不同的数值，以适应各种不同场合对特定谐波的补偿需求。与传统的重复控制相比，该重复控制具有占用内存单元数目更少、动态性能更佳的优点，并为各种场合的重复控制器提供了一种通用的表达式。最后将谐波补偿重复控制应用于单相逆变器的波形控制中，并进行了仿真验证，表明了谐波补偿重复控制的优越性。

2 谐波补偿重复控制

2.1 内模改进

传统的重复控制器通过构造周期为L0的任意周期信号的内模，并将其嵌入闭环控制系统中，以实现对周期输入信号和扰动的无差跟踪补偿。传统重复控制的内模为

这是一个正反馈延迟环节，其等效结构原理图如图1所示。

图1 传统重复控制的内模模型Fig.1 The internal model diagram of CRC

将该内模嵌入开环系统的前向通道上便构成了传统的重复控制系统。本质上，内模的作用是为系统提供了无穷多个位于各谐波频率的极点，且在这些极点处内模的增益为无穷大，从而能够对谐波信号实现无静差补偿。将L0=2π／ω0（ω0为基波角频率）带入式（1）可得：

由式（2）可知，常规重复控制器的极点位于 lω0（l=1，2，3，…）处，即包含了基波频率和所有的谐波频率。因此，如果将基波频率设置为nω0（n=1，2，3，…），重复控制器的极点将位于 nlω0，此时重复控制器内模变为

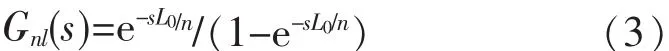
本文将以式（3）作为内模的重复控制器定义为nl次谐波补偿重复控制器。由自动控制原理的频移特性可知，将 Gnl（s）分别向左、右平移 mω0（m=1，2，3，…）可得：

由式（4）可见，Gnl±m(s)的极点在 Gnl(s)的基础上分别向左、右平移了 mω0，位于(nl±m)ω0处，即在 nl±m倍频处。由于以Gnl±m(s)作为内模的重复控制器在nl±m倍频处具有无穷大的增益，因此可以对nl±m次谐波实现无静差补偿。式（4）在理论上虽然成立，但是实现起来较为困难。为此，还需要寻求一种易于实现的内模形式。

由内模原理可知，只要描述内模的传递函数包含了周期输入信号的某些特定极点，即可对这些特定频率的谐波实现无静差补偿。为此，采用文献［8］和文献［9］的方法，将 Gnl+m(s)与 Gnl-m(s)作如下形式的加和

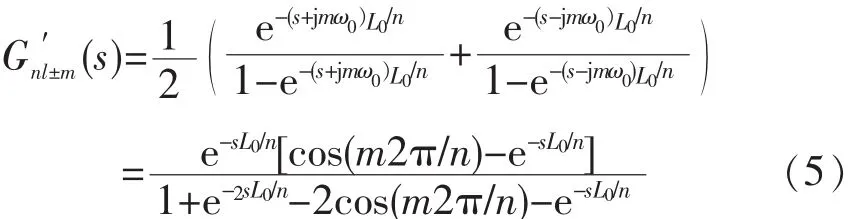
式（5）表示的内模，其极点仍然处于nl±m倍频处，同样可以实现对nl±m次谐波的无静差补偿。根据实际系统的需要，可为n和m设置不同的数值，即可得到相应的特定谐波补偿重复控制器。值得注意的是，这里的n和m需满足一定的约束条件，即n＞m≥0，n和m均为整数。例如，将n和m的数值分别设置为1和0，就可得到传统的重复控制器内模；将n和m分别设置为4和1，就将得到奇次谐波补偿重复控制器内模；而将n和m分别设置为6和1，此时将得到6l±1次谐波补偿重复控制器内模。可见，nl±m次谐波补偿重复控制器内模为所有重复控制器提供了一个通用的形式，而传统的重复控制器内模可看作是nl±m次谐波补偿重复控制器内模的一个特例，因此本文将(s)定义为 nl±m 次谐波补偿重复控制器内模。nl±m次谐波补偿重复控制内模的频域等效结构如图2所示。

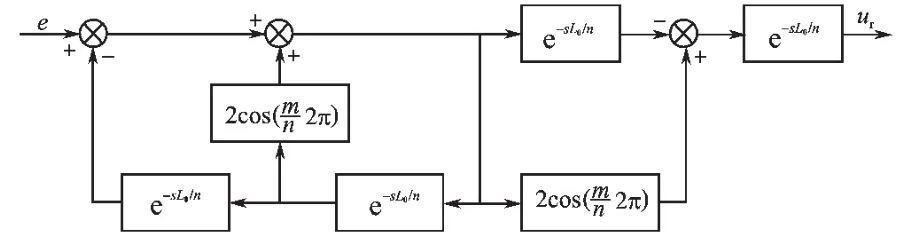
图2 谐波补偿重复控制内模的频域等效结构Fig.2 The internal model of HCRC based on S-domain

由图2可见，从nl±m次谐波补偿重复控制器内模的输入到输出的最大时间延迟为2L0/n，只要n＞2，其时间延迟将比传统的重复控制器内模更小。因此，nl±m次谐波补偿重复控制的动态响应速度要比传统的重复控制更快，将显著提高对谐波扰动的补偿速度，这是它相对于传统重复控制器内模的一大优点。

随着高性能的数字信号处理器的出现，重复控制大都采用数字化控制的方式来实现。与传统的重复控制一样，nl±m次谐波补偿重复控制器内模也采用数字方式。图3给出了nl±m次谐波补偿重复控制内模的离散等效结构。

图3 谐波补偿重复控制内模的离散等效结构Fig.3 The internal model of HCRC based on Z-domain

其离散传递函数为

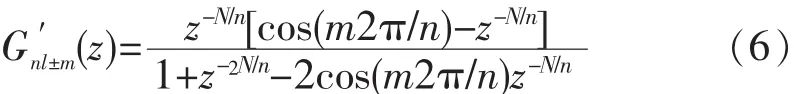
式中：N 为每周期的采样次数，N=fs/f0，fs，f0分别为采样频率和基波频率。

由式（6）可见，nl±m次谐波补偿重复控制器内模所需要的内存数目为2N/n，只要n＞2，将节约很大的内存空间，这是它相对于传统重复控制器内模的另一大优点。

与传统重复控制器类似，式（6）所示的nl±m次谐波补偿重复控制器内模是一种理想形式，它给系统引入的极点均位于单位圆上，因此极易出现失稳的情况。为此，可采用与传统重复控制器相同的方法，为分母上的各周期延迟环节串联一个Q加以改进，将极点限制在单位圆内，以增强系统的稳定性。改进后的nl±m次谐波补偿重复控制内模等效结构图如图4所示。

图4 改进的谐波补偿重复控制内模离散等效结构Fig.4 The improved internal model of HCRC based on Z-Domain

改进后nl±m次谐波补偿重复控制器内模的离散传递函数为

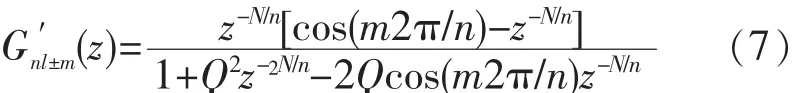
其中，Q可取小于1的常数或低通滤波函数。

改进后的nl±m次谐波补偿重复控制器内模在nl±m倍频处的增益将变为有限值。由式（7）可得：

以n=4，m=1时的奇次谐波补偿重复控制为例，当基波频率f0=50 Hz、采样频率fs=10 kHz时，其内模分别在Q=0.8和Q=0.95时的增益如图5所示。从图5中可以看出，奇次谐波重复控制内模在(4l±1)ω0处的增益分别为 5 dB 和 22 dB。

图5 4l±1次谐波补偿重复控制内模增益Fig.5 The internal model gain of HCRC for 4l±1 harmonic

可见，随着Q的减小，nl±m次谐波补偿重复控制器内模增益也逐渐降低，对谐波的补偿效果变差，跟踪误差变大。与常规重复控制器一样，这也是为增强稳定性而牺牲零静差特性的表现。

2.2 谐波补偿重复控制系统

在上述改进内模的基础上添加稳定化补偿器 Gc（z）和相位补偿环节 Gf（z）即可构成 nl±m 次谐波补偿重复控制器。将该重复控制器嵌入闭环控制系统的前向通道上便构成了nl±m次谐波补偿重复控制系统，如图6所示。其中，r（z）为周期参考输入信号，e（z）为跟踪误差，ur（z）为重复控制器输出的控制信号，d（z）为扰动信号，u（z）为系统输出信号，Gc（z）为稳定化补偿器，Gf（z）为相位环节，GCHRC（z）为 nl±m 次谐波补偿重复控制器，Gp（z）为被控对象。

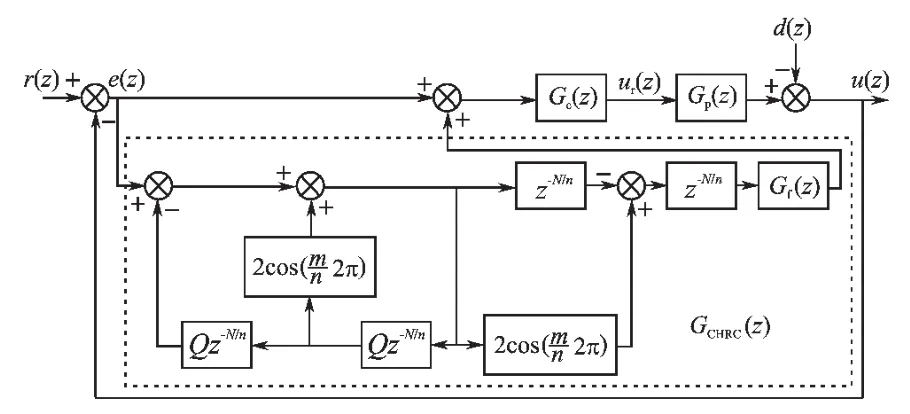
图6 嵌入式谐波补偿重复控制系统Fig.6 Diagram of plug-in HCRC system

由图6可得nl±m次谐波补偿重复控制系统的实际输出为

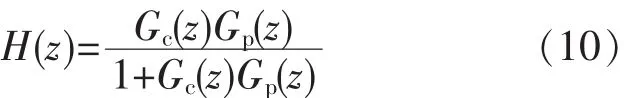
由式（9）和式（10）可得 nl±m 次谐波补偿重复控制系统的稳定性条件： 1）Q是稳定的；2）H(z)是稳定的有理函数，即 Gc（z）和 Gp（z）没有零极点对消；3）

为了获得最佳的零相移补偿效果，Gf（z）通常选作 H（z）的逆传函［10－11］。 但是，在实际应用中，由于对象建模的诸多不确定因素和负载的变化，因而无法获得H（z）的精确传递函数。为此，可将H（z）的实际逆传函表示如下［11］：

式中：Gfn（z）为 H（z）的理想逆传函，Gfn（z）=1/H（z）；△（z）为描述系统不精确性的稳定变量，且 △（z）有界，|△（ejω）|≤ε，ε 为大于零的常数。

将式（8）和式（11）带入式（9）可得 nl±m 次谐波补偿重复控制系统的实际输出为

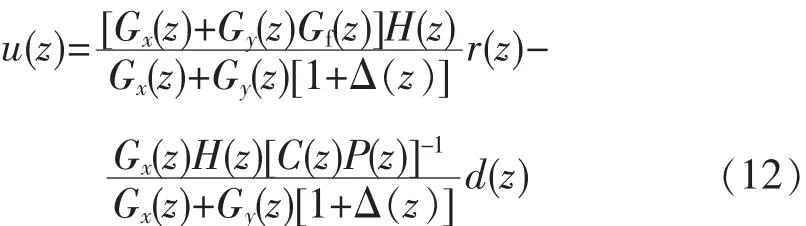
其中

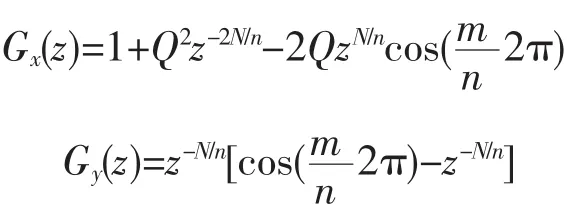
当Q=1时，式（12）的第1项在nl±m倍频处等于r(z)，第 2项等于 0，因此，nl±m 次谐波补偿重复控制可以实现无差补偿nl±m次谐波的控制目标。

3 仿真实验

为了验证谐波补偿重复控制的正确性和有效性，将其应用到单相逆变器的波形控制中，并在Matlab/Simulink仿真平台下进行一系列仿真实验。由于整流负载给单相逆变器带来的主要是奇次谐波，因此在nl±m次谐波补偿重复控制器中令n=4，m=1，4l±1次谐波补偿重复控制能够对所有奇次谐波实现高精度补偿。实验中用到的逆变器参数为：直流输入电压Udc=380 V，额定输出电压U0=220 V，基波频率f0=50 Hz，采样频率fs=10 kHz，滤波电感L=0.7 mH，滤波电感等效电阻r=0.1 Ω，滤波电容C=36 μF，突加阻性负载4.4 Ω，整流负载输出电阻24.2 Ω，整流负载输出电感2 mH，整流负载输出电容470 μF。

单相逆变器的离散传递函数为［3，12］

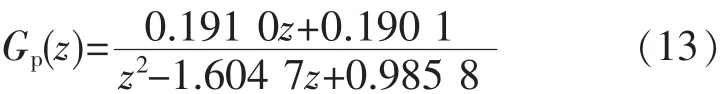
由于控制对象存在高谐振峰，给控制器的设计带来极大不便。为了简化控制器的设计，采用文献［13］中的输出电压微分反馈控制方法。其中，反馈系数k=6.1361。由此设计相位补偿环节Gf(z)=z6。

本文采用的稳定化补偿器为

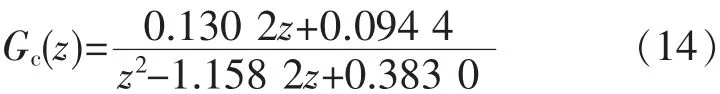
图7给出了仅采用式（14）所示的稳定化补偿器Gc(z)时逆变器的稳态输出电压、电流和相应的谐波分析。由图7a可以明显看出，输出电压有严重的平顶现象，波形畸变严重；通过谐波分析发现，引起输出电压畸变的谐波分量主要集中在4l±1次频率处，如图7b所示。

图7 Gc(z)作用下带整流负载时的输出波形及谐波分析Fig.7 The output waveforms and harmonic analysis with stabilization compensator

图8所示为逆变器在传统重复控制作用下带整流负载时的稳态输出电压、电流及谐波分析。由图8a可见，引入重复控制以后，逆变器带整流性负载时的输出电压波形得到了明显的改善，其波形的正弦性较好，平顶现象得到了消除；由图8b可见，重复控制器对于原有的奇次谐波的抑制效果非常明显，总谐波畸变率被降至0.91%。

图8 CRC作用下带整流负载时的输出波形及频谱分析Fig.8 The output waveforms and harmonic analysis with CRC

图9为逆变器在4l±1次谐波补偿重复控制作用下带整流性负载时的稳态输出波形及输出电压谐波分析。从图9a可以看出，逆变器在奇次谐波补偿重复控制下仍然有着良好的稳态输出，说明该控制方案对于整流性负载给逆变器带来的奇次谐波扰动具有较好的补偿效果；从图9b显示的输出电压谐波分布可以看出，与图8b相比，在4l±1次谐波补偿重复控制下，输出电压波形中 4，6，8，10，12 次谐波成分有少量的增加，因而总谐波畸变率也有所上升，但是只有1.30%，仍然较低。因此，奇次谐波补偿重复控制同样保证了逆变器的稳态输出质量。

图9 HCRC作用下带整流负载时的输出波形及频谱分析Fig.9 The output waveforms and harmonic analysis with HCRC

图10示出了逆变器分别在传统重复控制和4l±1次谐波补偿重复控制作用下突加阻性负载时输出波形的动态恢复过程。从图10a可以看出，在传统的重复控制作用下，输出波形大约需要4～5个基波周期才能恢复稳定状态；从图10b可以看出，在4l±1次谐波补偿重复控制作用下，输出波形大约需要2～3个基波周期即可恢复稳定状态。由此可见，4l±1次谐波补偿重复控制的动态响应速度比传统重复控制要快，其误差收敛所需时间更短。

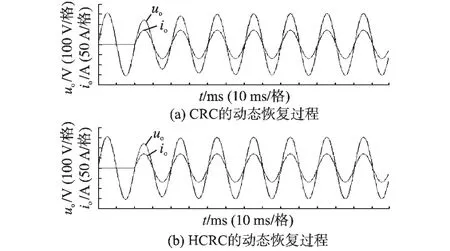
图10 CRC和HCRC的动态恢复过程Fig.10 The dynamic response of CRC and HCRC

4 结论

相比于传统的重复控制，本文提出的谐波补偿重复控制具有占用内存单元少、动态响应速度快、误差收敛时间短的优点。

仿真结果表明，尽管4l±1次谐波补偿重复控制在降低输出电压THD上比传统重复控制稍显逊色，但是其误差收敛速度却快了近2倍，而数字化控制系统占用的内存空间也减少了一半。因此，谐波补偿重复控制在基于周期的控制系统中是一种高性价比的控制方案。

［1］Francis B，Wonham W.The Internal Model Principle for Linear MultivariableRegulators［J］.AppliedMathematicsOptimization，1975， 2（2）：170-194.

［2］Paolo Mattavelli，Fernando Pubhabel Marafao.Repetitive-based Control for Selective Harmonic Compensation in Active Power Filters［J］.IEEE Transactions on Industrial Electronics， 2004，51（5）：1018-1024.

［3］Zhang Kai，Kang Yong，Xiong Jian，et al.Direct Repetitive Con⁃trol of SPWM Inverter for UPS Purpose［J］.IEEE Transactions on Power Electronics， 2003，18（3）：784-792.

［4］Freema n C， Tan Y.Iterative Learning Control and Repetitive Control［J］.International Journal of Control， 2011， 84 （7／9）：1193-1195.

［5］Chen Wentao，Lin Yechun.Repetitive Control Design for Optimal Performance［J］.Asian Journal of Control， 2011， 13（6）：1051-1055.

［6］Costa-Castello R，Grino R.A Repetitive Controller for Discretetime Passive System［J］.Automatica， 2006， 42（9）： 1605-1610.

［7］Zhou Keliang，Kay-Soon，Wang Danwei，et al.Zero-phase Oddharmonic Repetitive Controller for a Single-phase PWM Inverter［J］.IEEE Transactions on Power Electronics， 2006， 21（1）：193-201.

［8］Gerardo Es Cobar， Perla G Hernandez-Briones， PanFilo R Martinez，etal.ARepetitive-basedControllerforthe Compensation of 6l±1 Harmonic Components ［J］.IEEE Transactions on Industrial Electronics， 2008， 55（8）： 3150-3158.

［9］Etxeberria-Otadui I，Lopez-de-Heredia A， Gaztan～aga H，et al.A Single Synchronous Frame Hybrid （SSFH）Multifrequency Controller for Power Active Filters ［J］.IEEE Transactions on Industrial Electronics， 2006， 53（5）： 1640-1648.

［10］G rin～ó R， Costa-Castelló R.Digital Repetitive Plug-in Controller for Odd-harmonic Periodic References and Disturbances［J］.Automatica，2005，41（1）：153-157.

［11］Zhou Keliang，Wang Danwei，Zhang Bin.Plug-in Dual-modestructure Repetitive Controller for CVCF PWM Inverters ［J］.IEEE Transactions on Industrial Electronics， 2009， 56（3）：784-791.

［12］Rymarski， Zbigniew.Design Method of Single-phase Inverters for UPS Systems［J］.InternationalJournalofElectronics，2009，96（5）：521-535.

［13］Lei Q，Peng F Z， Yang S.Multiloop Control Method for Highperformance Microgrid Inverter Through Load Voltage and Current Decoupling with Only Output Voltage Feedback ［J］.IEEETransactions on Power Electronics，2011，26（3）：953-960.