基于ANSYS的EBZ200型掘进机回转机构的有限元分析
2013-06-25申丽兵崔卫秀
申丽兵,崔卫秀
(阳泉煤业集团和顺新大地煤业有限公司职工学校,山西 和顺 032700)
0 引 言
悬臂式掘进机在煤矿隧道掘进中的逐步推广和大量使用,提高了工作效率和经济效益,已成为主要产煤国家不可缺少的设备。悬臂式掘进机中的回转机构,一方面承受着工作机构所有的切割阻力和阻力矩,一方面完成着工作机构的水平进给运动(回转耳架及摆动油缸组成)。它的可靠性和稳定性直接关系到整机的使用周期,其尺寸大小也直接影响到整机的高度和宽度等总体参数。传统设计中,回转机构的设计计算通常采用解析法,其对简化计算、初始设计有一定的理论意义,但是由于摆动油缸受到油液冲击载荷的影响,以及截割矿岩时的载荷是变化的,回转机构受的力矩并不是定值。EBZ200型悬臂式掘进机有截割功率大、重心低、结构紧凑、调动灵活等特点。回转机构是其重要部件,它连接机架、支撑截割臂,实现截割头的钻进掏槽、扫落煤岩、截割臂的升降、回转等运动,并承受来自截割头的复杂多变的冲击载荷,因此它的性能将直接关系到掘进机的稳定性及工作效率[1]。
本文利用CAD建模软件Unigraphics,对悬臂式掘进机回转机构对实际结构尺寸建立了三维实体模型;然后利用有限元分析软件ANSYS Workbench对回转机构中的关键零件进行了应力-应变分析,得到了回转耳架在实际工况下的应力和变形分布,为进一步的结构优化奠定了基础。回转机构的有限元分析过程如下。
1 材料属性的添加及单元的划分
有限元初始模型先要添加材料属性及划分网格。回转耳架添加材料属性,见图1。
ANSYS软件对网格的划分有两种:1)自由划分网格(FreeMeshing)对于单元形状无限制,内部节点位置较随意,在其体上可自动生成四面体网格。2)映射网格划分(MappedMeshing)生成的单元形状较规则,必须包含六面体、五面体、四面体单元,在相对的面和边上所定义的单元划分数必须相等,对于复杂边界模拟能力较自由划分网格差。如果要采用循环对称法计算,则采用六面体单元,必须用映射分网。因为回转耳架模型不规则,故选用自由网格划分法。

图1 材料属性对话框
有限元法是用有限个单元将连续体离散化,采用数值计算方法分别计算每个单元,属近似计算方法。如果划分网格较密集,或者划分单元形式正确,则计算结果与理论结果较相近。如果网格加密,可能获得更加精确的结果;但因网格过密,又会造成计算量过大、计算时间过长、结果精度并未提高很多,需要综合考虑各方面的因素。假如网格精度适当,较小的网格精度也能得到精确结果[2]。
ANYSYS提供了多种网格划分格式,常用的有四面体实体单元、三角形实体单元,以及六面体实体单元。这些划分算法中又分为线形和抛物线形,抛物线形的接点多于线形的接点,因此计算精度高,但占用计算机的资源多,计算时间较长。因为回转耳架是用三维实体建模,采用抛物线形四面体实体单元划分、局部加密,以便精确算出这些部位的应力[3]。本文利用AN⁃SYS Workbench自动划分网格,得到初始网格结果,并在各铰接点处细化网格,最终结果见图2。从图2看出,模型共有61 144个节点,33 594个四面体单元。

图2 网格划分结果
2 约束与载荷的添加
考虑到回转耳架与回转轴承采用的是螺栓联接,对回转耳架的回转中心添加全约束,对各个铰接点按照动力学仿真结果中的平均值,分别按照轴向力、径向力、竖直方向力添加载荷。当模型、网格、约束、加载均已完成后,采用稀疏矩阵法(Sparse Solver)对其求解。分析所得结果[4],见图3。从图看出,回转耳架的最大应力接近于不同部件的焊接处和有角的部位,这与回转耳架实际损坏部位符合,故在后续加工中,应增加焊口强度。

图3 载荷添加
3 有限元的结果分析
经过前期准备,得到模型等效应力分布见图4,变形趋势见图5。结果显示,回转耳架最大等效应力67.204 MPa,最大变形1.030 2 mm。根据《机械设计手册》查得 ZG45的许用应力:[σ]=0.2σs=0.2×370=74 MPa,由于67.204 MPa<[σ],结构安全。但是,由于对模型所施加的载荷为掘进机运行平稳时的平均值,最大应力已经逼近许用应力,如果掘进机在工作时剧烈震荡,或者截割煤岩硬度较高(本模型截割负载15 t),很有可能达到或超过许用值,故在今后的结构和尺寸设计时,应该考虑避免这种状况的出现[5]。

图4 等效应力分布云图
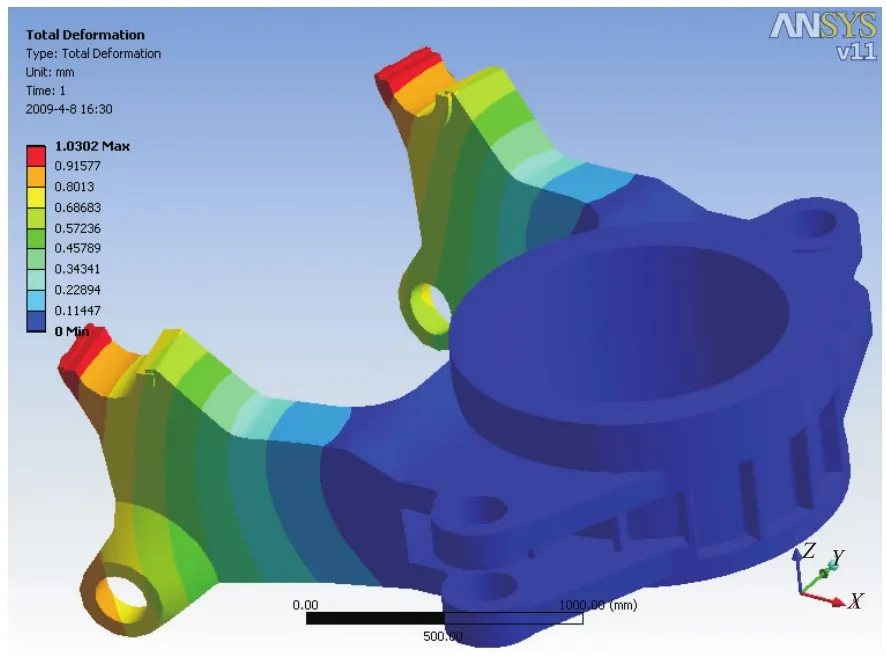
图5 受力变形云图
[1] 马跃.谈我国悬臂式掘进机的发展及趋势[J].煤,2005,15(2):29-32.
[2] 赵经文.结构有限元分析[M].北京:科学出版社,1986.
[3]黄燕.横轴式掘进机动态模型的建立及动力学行为的研究[D].阜新:辽宁工程技术大学,2002:12-16.
[4] 王成,邵敏.有限单元法基本原理和数值方法[M].北京:清华出版社,1997.
[5] 高德平.机械工程中的有限元法基础[M].西安:西北工业大学出版社,1993.
