调度策略在并行机调度仿真的应用

王 崐，郑树琴

（1.山西省煤炭规划设计院，山西 太原 030045；2.太原理工大学机械工程学院，山西 太原 030024）

0 引 言

调度是在有限生产资源约束中优化效益目标函数的决策过程。多机调度旨在为一系列工作的加工处理过程建立适当的调度次序，以保所有工作在合适的时间内完成；在此过程中需要解决的问题包括：机器的分配、工作处理次序、调度合理性等。多机调度问题分为针对并行机和串行机，均被证明为NP-hard问题[1]。并行机调度可按系统配置分为三种：等同机、同类机、变速机的调度。实际调度需要考虑系统随机性和动态性的影响[2]，例如：加工时间的不确定性和订单到达率随时间的动态性。大型系统的多目标调度时常出现，需要深入研究；因此文章建立仿真模型模拟动态随机环境中的等同机调度，进而研究不同策略在此系统中的作用，以求达到同时最大化吞吐率和最小化延迟工件量的双重目的。

多目标调度问题应用广泛，但其理论研究有待完善。Andres等[3]提出了多目标遗传算法解决流水车间调度问题，目标函数包括最小化调度时长和拖期，模型约束包括基于工序排序的调整时间和顺序的约束。Lee和Asllani[4]针对工序的调整时间的最小化拖期工件量和调度时长的单机调度问题，建立了混合整数规划模型及相关遗传算法。Jungwattanaki等[5]采用遗传算法和模拟退火算法，解决工序的调整时间的最小化加权调度时长和拖期工件量的流水车间调度问题。Picard和Queyranne[6]将单机调度问题建模成时间相关的旅行者问题（Traveling Salesman Problem）并运用分支定界法求解，以达到最小化拖期和加权拖期的目的。Allahverdi等[7]描述并解释了基于准备时间的多准则调度问题的复杂度。因此，最大化生产率和最小化延迟工件量的多目标并行机调度问题需要更重视。Kiran陈述了仿真方法对于随机动态调度问题的适用性。随机动态调度环境中，并非所有工作在同一时间进入生产系统，而且订单数量、加工时间、准备时间等变量都有随机性，因此利用仿真将调度策略用于不同的工作车间调度（比如Gupta等[8]，Tavakkolo-Moghad⁃dam等[9]和Ying[10]）。据上综述，多目标随机动态等同机调度问题很有实用价值，将用仿真方法分析随机动态环境中的调度问题。

1 研究方法

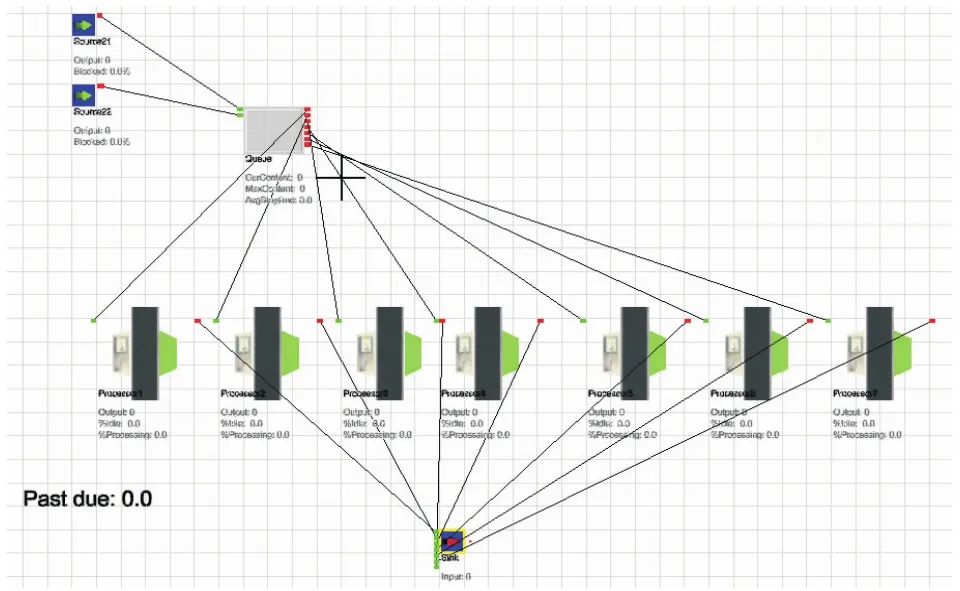
图1 仿真模型的配置和布局

文中制造系统的并行机调度模型是用Flexsim仿真软件，它是一款能帮助可视化流程优化生产和最小化运作费用的基于真实对象的仿真软件，可用来建立并分析随机系统离散事件仿真模型，可供仿真3D动画，并有强大数据收集和结果分析功能。仿真模型的布局和参数，基于某大型制造企业的组装车间，具有7条等同功能的生产线，包含多个装配步骤、加工时间较长，因此准备时间和加工时间中的不确定性和随机性较大；而且订单到达速率按时间而不同、产生了动态性，增加了调度求解的难度。Flexsim仿真模型的建立，基于组装车间实际布局的研究分析；模型参数及输入数据的统计分布，来自于车间实际数据的采集和前期分析，以保仿真模型具有很强的理论和实践价值。模型的配置和布局见图1，由于车间白班和夜班的订单到达率及加工速率都不同，因此采用不同的统计分布输入量。为了尽可能模拟车间实际情况，订单到达时间采取经验分布。订单的相关信息（比如订单数量、到达时间、交货期、迟到时间等）在订单生成的同时随机分配给每张订单；每张订单可被7条生产线中的任何一条加工、并且预期加工时间与生产线的选择无关，即生产实际中加工时间的随机性（方差）在调度策略中被忽略。

每张订单的实际加工时间：

订单实际加工时间=准备时间+

（工件标准加工时间+调整因子）×订单数量.（1）

式中：加工时间的随机性由调整因子表示，代表了实际加工时间与标准时间的偏差，来自不同生产线的配置（机器设备配置、工人熟练程度等）；调整因子的数值大小来自于一个Johnson Bounded分布的随机变量，而此统计分布的参数拟合源于该车间的实际生产数据分析。该模型的仿真时间设置为24 000 min，即20个工作日。模型预热时间为2 400 min，即2个工作日。每个模型重复10次，以对仿真结果进行统计分析。模型参数的设置见表1。实际数据统计期间，33个工作日的实际产量为1 261。根据表1参数设置，当重复10次仿真模型、并且每次运行42 000 min（包含2 400 min的预热时间）时，运用先入先出（FIFO）调度策略（车间现行实际调度策略）的仿真输出结果的产量平均值为1 232，90%置信区间为[1 178,1 287]，即仿真结果的置信区间包含了实际产量（1 261）。此结果验证了本文仿真模型的正确性。

表1 Fl e x s i m仿真模型参数设置

2 结果分析

本文依据仿真模型和参数设置，采用不同调度策略所得仿真结果见表2，调度策略包括：先入先出（FIFO）、最小化加工时间优先（SPT）、最早订单完成时间优先（EDD）。其中FIFO是车间实际使用的调度策略，也是很多企业最常用的调度策略。表2列出基于单一目标（最大化生产率或最小化拖期工件量）和多目标时最优调度策略的仿真结果。多目标函数定义按式（吞吐率）：

α×拖期工件量；其中：0﹤α﹤1. （2）式中：多目标函数的含义是：最大化调整吞吐率，即在总生产率中减去拖期工件带来的罚值，此罚值与拖期工件量成正比，罚值的权重α介于0和1之间，取决于企业中拖期工件的管理成本。本次试验α选定值0.5。

表2考虑单一目标函数进行对比策略时，SPT策略对于分别最大化生产率和最小化拖期工件量均可达到最优。EDD策略相较现行策略FIFO在控制拖期工件量方面有一定优势，但是在结果中的总产量并不因策略的改变而增加，反而会因为过度考虑优化拖期订单而以牺牲吞吐量为代价。

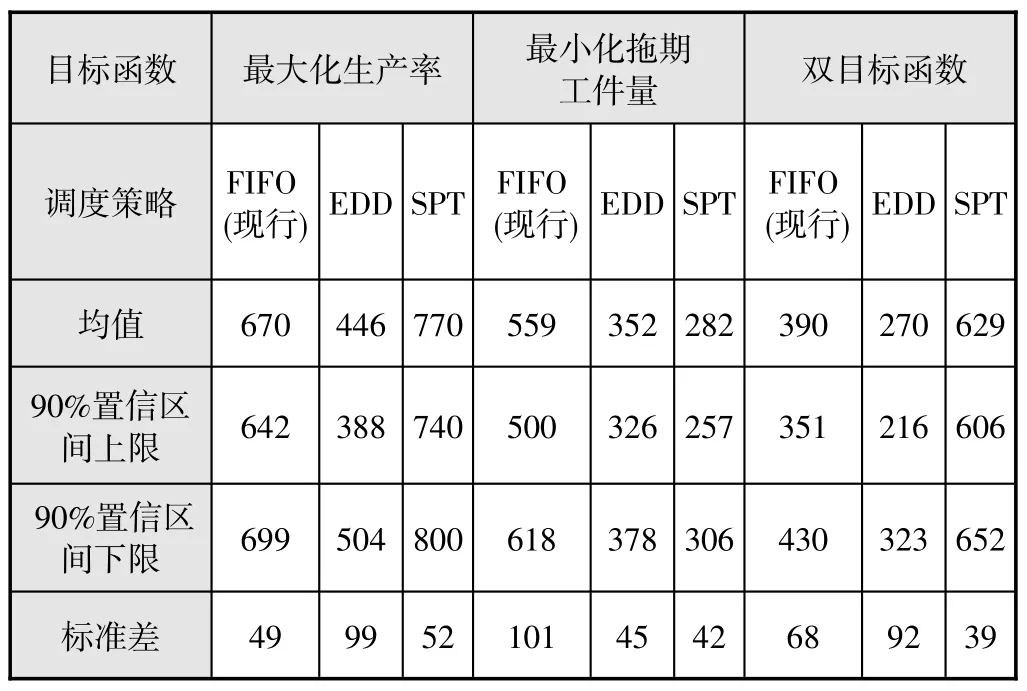
表2 Fl e x s i m仿真实验结果

当按式（2）的多目标函数时，SPT策略仍有很大优越性是不仅试验期间目标函数结果的均值优势于策略FIFO和EDD，而且表中结果的标准差也明显降低。总之，应用SPT策略可显著提高系统产出的均值，同时降低输出结果的不确定性（即标准差），从而提高系统的可靠性。

由于SPT策略对提高系统产量和可靠性的表现显著，表3将SPT策略对比现行FIFO策略的优越性进行了总结。绝对提高量是运用各评价指标时SPT结果和FIFO结果均值的差，相对提高量则定义为式（3）：

式中：代入的数值为表2中仿真结果的均值。表3结果表明，如果企业采用SPT策略在其等同机车间内，生产系统的效率将大幅提高；仅考虑吞吐率为目标时，SPT策略带来的增幅为14.9%；拖期工件数量单一目标的减少为49.6%；如果考虑多准则多目标评价时，SPT策略的使用可以带来61.3%的显著提高。

表3 S PT策略相较于现行FI FO策略的生产提高量

3 结束语

本文针对动态随机环境，运用调度策略建立了并行机调度问题的仿真模型；该等同并行机调度问题以最大化吞吐率和最小化延迟工作数量为多目标函数。此仿真模型用于一个7台等同并行机的装配车间，模型参数和实验数据来自某大型制造企业。仿真结果与实际数据结果的比较证明了仿真模型的正确性。仿真结果分析进而表明：最小化加工时间优先（SPT）的调度策略相较现行的先入先出（FIFO）策略，在生产输出量和可靠性上都有显著提高。因此，大型动态随机环境的生产系统中，适当改变现行调度策略，加入新的调度策略或调度算法，可大幅提高系统的效率和可靠性。

[1] Cheng,T.C.E，Sin,C.C.S.A state-of-the-art review of paral⁃lel-machine scheduling research[J].European Journal of Op⁃erational Research，1990（47）：271-292.

[2] Banks,J.Handbook of simulation:principles,methodology,ad⁃vances,applications,and practice[M].Wiley,New York.1998.

[3] Andres,C.,Tomax,J.V.,Garcia-Sabater,J.P.and Miralles,C.,A multi-objective genetic algorithm to solve the schedul⁃ing problem in flowshops with sequence dependents setup times[J].Proceedings of the International Conference on In⁃dustrial Engineering and System Management,Marrakech,Morocco,May 2005（16-19）：630-635.

[4] Lee,S.M.and Aslani,A.A.Job scheduling with dual criteria and sequence-dependent setups[J].Mathematical versus ge⁃netic programming.Omega，2004（32）:145-153.

[5] Jungwattanaki,J.,Reodecha,M.,Chaovalitwongse,P.and Werner,F.An evaluation of sequencing heuristics for flesible flowshop scheduling problems with unrelated parallel ma⁃chines and dual criteria[J].Otto-von-Guericke-Universitat Magdeburg,2005,28（5）：1-23.

[6] Picard,J.C.and Queyranne M.The time-dependent traveling salesman problem and its application to the tardiness problem in one machine scheduling[J].Operational research,1978（26）：86-110.

[7] Allahverdi,A.,Gupta,J.N.D.and Aldowaisan,T.,A review of scheduling research involving setup considerations.Omega[M].Int.J.Mgmt Sci.,1999（27）：219-239.

[8] Gupta,A.K.,A.I.Sivakumar.Simulation based multiobjective schedule optimization in semiconductor manufacturing[M].In Proceeding of the 2002 Winter Simulation Conference,ed.E.Yucesan,C.-H.Chen,J.L.Snowdon,and J.M.Charnes,IEEE,Piscataway,New Jersey:2002:1862-1870.

[9] Tavakkoli-Moghaddam,R.and M.Daneshmand-Mehr.A computer simulation model for job shop scheduling problems minimizing makesapn[J].Computers＆amp;Industrial Engineering 2005（48），2002：811-823.

[10] Ying,C.C.,1996,Specification of a job shop scheduling sim⁃ulation model and some properties of its internal transition function[J].Computers ind.Engng,1996（31）：201-204.