基于UG的渐开线直齿圆柱齿轮参数化精确造型设计
2013-06-25李小明
祝 林,李小明
(四川职业技术学院,四川 遂宁 629000)
0 引 言
在工程机械中用作传动的渐开线直齿圆柱齿轮应用相当广泛,对直齿圆柱齿轮进行精确造型设计是工程机械进行承载分析、性能分析和动力学分析的难点。
直齿圆柱齿轮的齿廓曲线比较复杂,包括齿根圆弧、齿根过渡曲线、渐开线和齿顶圆弧。尤其是齿根部分的过渡曲线,齿轮的加工方式不同,所形成的过渡曲线也不一样。为了得到精确的齿廓曲线,必须通过数学模型来描述齿廓的各段曲线,并结合UG表达式强大的参数化功能实现其精确造型设计。
1 U G的参数化设计理念
UG是一款集CAD/CAM/CAE于一体的高端软件,功能覆盖了从概念设计到产品生产的整个过程,广泛应用于汽车、航空、航天、模具设计、医疗器材等各个领域。其强大的参数化设计功能,使得复杂实体造型成为可能。所谓参数化设计就是对零件上各个特征施加各种约束,各个特征的几何形状与尺寸大小用变量参数的方式来表示,如果定义某个特征的变量参数发生了改变,则零件的这个特征的几何形状或尺寸的大小将随参数的改变而改变。通过把参数、关系和参照元素等零部件设计意图融入到图形模型里,利用多组参数驱动零部件的特征尺寸和位置尺寸以完成其三维建模;通过对参数的不同赋值实现对三维模型的重建或修改。UG进行参数化设计采用由算术或条件语句构成的表达式,通过UG的表达式建立齿廓曲线方程和与齿轮几何尺寸相关的计算公式,生成齿廓曲线,并通过特征操作实现齿轮的完全参数化设计,精确建立齿轮的三维模型,从而提高齿轮的设计效率。
2 齿轮齿廓曲线的表达式的建立
2.1 基本参数表达式的建立
先在表达式对话框中输入齿轮和齿条形刀具的基本参数表达式[1],便于后面的表达式引用,具体为:
t=0//UG内部变量,变化范围0~1;
m=3//齿轮模数,建立不同模型时可以更改;
z=20//齿数,建立不同模型时可以更改;
c∗=0.25//顶隙系数;
r=m.z/2//齿轮的分度圆半径;
α=20°//渐开线在分度圆上的压力角;
invα=tanα-radα //渐开线在分度圆上对应的极角;
sa=m∗ (pi()/2-2h∗a∗ tan α )//齿条的齿顶厚;
sb=rb∗(pi()∗m/(2∗r)+2∗invα )//基圆齿厚;
pb=pi()∗m∗ cos(α )//基圆齿距;
rb=r∗cos(α)//基圆半径;
2.2 齿根圆弧表达式的建立
齿轮的齿根部分为一小段圆弧,根据齿根半径和角度范围可确定齿根圆弧直角坐标公式如下:

建立表达式为:
tf=deg(b*t/r)//齿根圆弧的角度范围;
rf=m*(z-2*h∗a-2*c∗)/2//齿根圆半径;
xf=rf*cos(tf)//齿根圆弧的x坐标;
yf=rf*sin(tf)//齿根圆弧的y坐标;
zf=0//齿根圆弧的z坐标;
2.3 过渡曲线表达式的建立
1)当渐开线齿轮范成加工时,刀具切入基圆所留下的轨迹,相当于刀具与齿轮之间的无间隙啮合运动。过渡曲线与齿轮加工方式有关,但其原理基本相同。标准齿条刀具顶部比普通齿条多出一段 c∗m,用于被加工齿轮的齿根部分切出齿顶间隙[2]。
现以图1所示齿条形刀具参数为例进行分析,刀具齿廓的顶部有两个圆角,cp是圆角的圆心,刀具各参数间具有以下关系:


式中:刀齿圆角半径rp,a为点 cp至中线的距离;b为点cp至齿形中心线的距离。
在用齿条形刀具加工齿轮时,节线ω绕节径为r的定圆做纯滚动,如图2所示,与节线固连的点E(刀齿圆角圆心)的运动轨迹 s1为延伸渐开线,s2为其等距线,齿轮的过渡曲线为 s2的一部分。根据几何关系,可得过渡曲线的直角坐标公式如下:

式中:ϕ为过渡曲线的摆角,α1为参变角。在过渡曲线的形成过程中 ϕ从0变化到最大值,ϕ的最大值公式和 α1与 ϕ的关系式为:

式中:αq为过渡曲线与渐开线相切点对应的压力角。 ϕ=0时,为避免α1的分母为零,xg,yg的表达式采用UG的if…else…的语法结构。过渡曲线的起始点(ϕ=0)应与齿根圆的终点相切,所以如图2所示的过渡曲线图形应逆时针旋转到 tf的最大值。
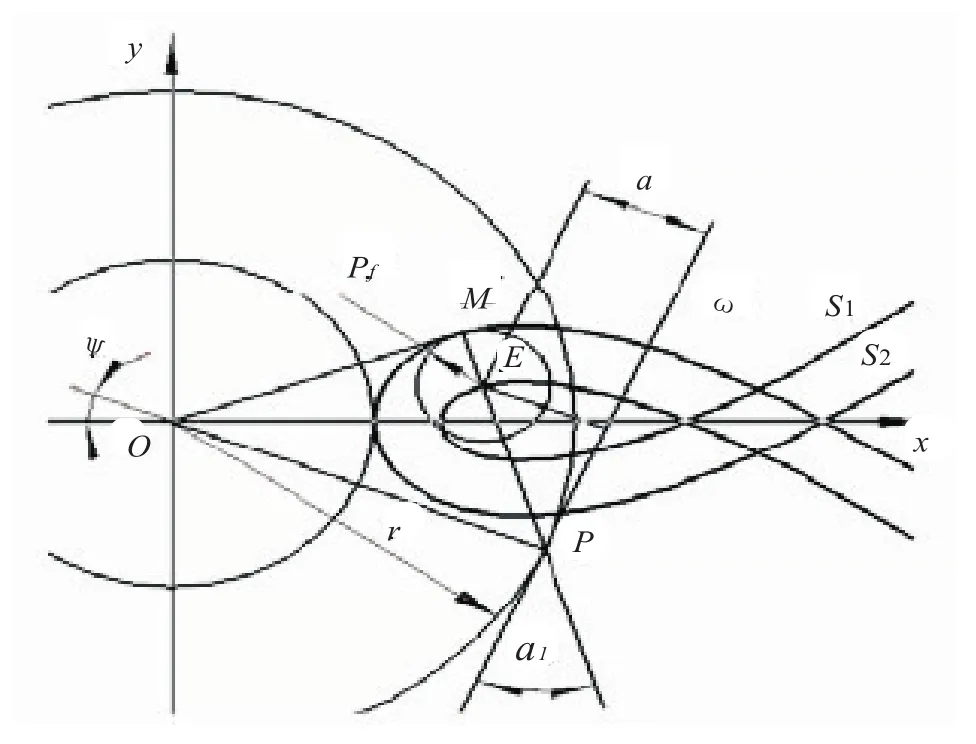
图2 过渡曲线形成示意图
2)根据以上分析,输入表达式为:
maxtf=deg(b/r)//tf的最大值图3渐开线形成示意图;
rq=sqrt(rb^2+(r*sin α -h∗a*m/sin α )^2)//过渡曲线与渐开线相切点对应的极径;
αq=arccos(rb/rq)//过渡曲线与渐开线相切点对应的压力角;
l=(rb*tanα-rb*tanαq)*cosα-sa/2+b//摆角对应的节圆弧长;
ϕ=deg(l/r)*t//过渡曲线的摆角
xg=if(t>0)(r*cos(maxtf-ϕ)-(a/sin((arctan(a/(r*rad ϕ))))+rp)*sin((arctan(a/(r*radϕ)))+(maxtf-ϕ)))else((r-a-rp)*cos(maxtf))//过渡曲线的x坐标;
yg=if(t>0)(r*sin(maxtf-ϕ)+(a/sin((arctan(a/(r*rad ϕ))))+rp)*cos((arctan(a/(r*radϕ)))+(maxtf-ϕ)))else((r-a-rp)*sin(maxtf))//过渡曲线的y坐标;
zg=0//过渡曲线的z坐标;
2.4 渐开线表达式的建立[3]
1)渐开线形成示意图,如图3所示,其直角坐标公式如下[3]:
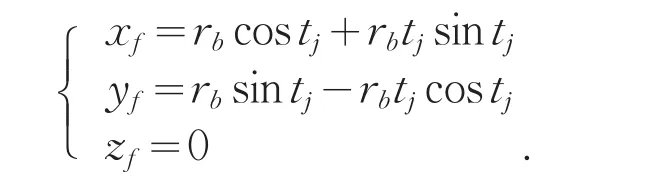
式中:tf=θj+ αj,θj为渐开线的极角,αj为渐开线的压力角。渐开线的起始点应与过渡曲线的终点相切,所以,图3所示的图形应逆时针旋转θb,经计算θb=(pb-sb)/2rb。渐开线的起始点是刀具的切出点,不一定在基圆上。

图3 渐开线形成示意图
2)根据以上分析,输入表达式为:
ra=(m*z+2*h∗a*m)/2//齿顶圆半径;
αj=arccos(rb/ra)//齿顶圆与渐开线交点处对应的压力角;
tj=deg(tan(αq+(αj-αq)*t))//tj的变化范围;
θb=deg((pb-sb)/(2*rb))//图形逆时针旋转角度;
xj=rb*cos(θb+tj)+rb*rad(tj)*sin(θb+tj)//渐开线x的坐标;
yj=rb*sin(θb+tj)-rb*rad(tj)*cos(θb+tj)//y坐标;
zj=0//z坐标;
2.5 齿顶圆弧表达式的建立
齿顶部分同样为一小段圆弧,其直角坐标公式如下:
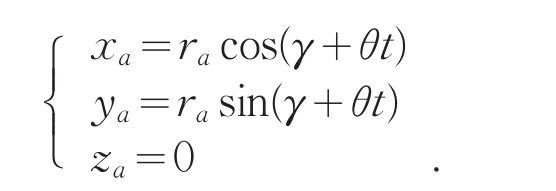
式中:ra为端面齿顶圆半径,γ为端面齿顶圆展角,θ为端面齿顶圆齿厚对应圆心角。表达式为:
γ=deg(tanαj-radαj)//αj处端面齿顶圆展角;
θ=deg(pi()/z)//端面齿顶圆齿厚对应圆心角;
xa=ra*cos(θb+invαj+(θ -(θb+invαj))*t)//齿顶圆弧的x坐标;
ya=ra*sin(θb+inv αj+(θ-(θb+invαj))*t)//齿顶圆弧的y坐标;
za=0//齿顶圆弧的z坐标;
3 参数化设计
3.1 参数化设计步骤
渐开线直齿圆柱齿轮参数化设计的关键是齿轮相关参数的建立,在UG中的设计过程如下[4]:
1)建立相互关联的表达式;
2)使用基本曲线功能中的规律曲线选项,通过方程式,并利用已经建立的表达式绘制出齿根圆弧、过渡曲线、渐开线曲线、齿顶圆弧,从而形成首尾相接的单个齿槽线串;
3)进入草图,以齿根圆弧的圆心画出齿顶圆,一定要用表达式来定义齿顶圆的直径;
4)利用相关的特征操作(拉伸、沿引导线扫描、沿圆周阵列)完成渐开线齿轮的三维建模。初始化齿轮,如图4所示。
3.2 表达式的生成
对直齿圆柱齿轮而言,其端面是渐开线,符合齿廓啮合基本定律,即可改变齿数z、模数m、压力角α等常用参数,可以得到不同的直齿圆柱齿轮的三维模型。齿轮参数化设计方法大体分两种:1)对现有软件进行二次开发,需要编程;2)利用UG软件已有的功能实现参数化设计,尤其UG具有强大的表达式功能。利用2)方法更具通用性,建立表达式可以用以下两种方式:(1)选择Tools>Expressions,直接输入表达式。(2)建立一个文件名称用英文字母或数字表示的纯文本文档,并输入相关的表达式,保存并关闭后更改文件扩展名为.exp;然后在UG中选Tools>Expres⁃sions>Import,输入建立.exp文件。
3.3 参数化实现
直齿轮的参数化实现要求齿轮能够实现在其设计要求发生改变时,它的结构尺寸也相应地改变以满足新的设计需要。为此,只需要将上述所建立的齿轮实体模型的相关特征参数进行更改,就可以生成各种相关参数的齿轮三维模型[5]。特征参数的修改可以利用以下方式:
1)将生成特征实体的参数生成数据文件,利用系统自带的UG/Open GRIP语言进行编程,实现对齿轮参数的修改。
2)利用UG系统所具有电子表格功能编辑、定义和修改相关表达式及参数,通过更新完成齿轮的自动建模,从而实现齿轮的可参数化控制。
3)最直接的方式是通过编辑表达式中的特征参数来实现齿轮模型的重新自动建模。选取需要更改的参数表达式,并重新对表达式直接修改来实现完全参数驱动。基本参数更改后的齿轮模型,如图5所示。

图4 初始化齿轮模型

图5 参数更改的齿轮模
4 结 论
本文所提的齿轮建模方法是以齿轮的轮廓曲线公式为依据,通过建立表达式控制曲线形状,并且通过表达式实现了参数化,所建立的模型与实际加工得到的齿轮形状相一致,实现齿轮的参数化设计和自动特征建模,提高渐开线圆柱直齿轮的设计效率和质量,为齿轮的力学分析、运动分析等做了符合实际的准备工作。本方法在UG8.0平台上实践通过。
[1] 张策.机械原理与机械设计[M].第2版.北京:机械工业出版社,2010.
[2] 吴继泽,王统.齿根过渡曲线与齿根应力[M].北京:国防工业版社,1989.
[3] 朱景梓,张展,秦立高.渐开线外啮合圆柱齿轮传动[M].北京:国防工业出版社,1990.
[4] 袁锋.使用UG软件的机电产品三维数字化设计教程[M].北京:高等教育出版社,2011.
[5] 孙江宏.基于UG的直齿圆柱齿轮参数化实体设计通用方法[J].机械科学与技术,2002(11):25-27.
