电液位置伺服控制系统传递函数模型研究

徐国强

（华晋焦煤有限责任公司，山西 太原 030001）

0 引 言

电液控制系统影响因素复杂,不能用精确模型来描述其所有特性，所以,在控制系统的分析和设计中,往往采用简化模型。因此,在所有基于模型的液压控制系统当中都几乎不可避免地存在未建模动态。推导液压动力元件系统方程时作如下假设：零开口四边滑阀的四个节流窗口匹配和对称；供油压力恒定；对阀的流量方程进行线性化；忽略管道中的压力损失和管道动态；油温和体积弹性模量为常数；不考虑库伦摩擦等。由于上述因素的存在，建立精确的数学模型是很困难的，只能建立一个近似的数学模型。在建模时，要作合理的近似处理，要忽略对象中的不确定因素，例如参数误差，未建模动态、测量噪声及不确定的外干扰等。

本文从电液位置伺服系统的基本原理出发，推导出电液位置伺服系统的微分方程与传递函数，为电液位置伺服系统的设计提供了依据。

1 电液伺服阀的非线性特性及线性化分析

1.1 通过对非线性微分方程线性化可以获得线性模型

设有如下形式的非线性表述：

式中：f(⋅)是围绕平衡点 xv0的解析函数，即：f(xv0)=0。如果 x(t0)=xv0，那么对于所有 t≥t0，x(t)=xv0+σx。δx表示相对xv0的小偏差量。考虑系统在x(t)=xv0+δx的性质：

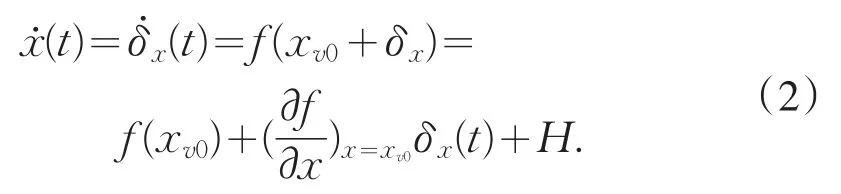
式（2）中：H表示高阶项，包括 (δx)2/2!，(δx)2/3!，…及f对x在xv0点估计值的高阶偏差量。当 ||δx→0时，高阶项的影响忽略，动态方程可用下式近似表示为：

伺服系统中四通零开口滑阀得到最广泛应用，故本文均以四通零开口滑阀为研究对象。在液压伺服系统中[1]，控制滑阀的负载流量QL是负载压力 pl及阀芯位移xv的函数，即QL=f(xv,pl)该函数是非线性的。具有匹配和对称节流窗口的理想零开口四边滑阀的稳态特性方程为：

则可用小位移线性化方法将式QL=f(xv,pl)线性化。设在某工作点(xv0,pl0)的负载流量是QL0,即：

QL0=f(xv0,pl0)，xv=xv0+Δxv，pl=pl0+Δpl则： QL=f(xv,pl)=f(xv0+Δxv,pl0+Δpl).

将式按台劳级数展开，假定工作点为零点：

则输出流量变化为：

为分析方便起见，认为位置伺服系统是在零位条件下工作的，用变量本身表示它们从初始条件下的变化量。且定义流量增益及流量-压力放大系数分别为

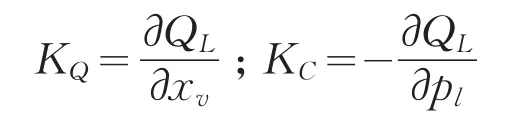
则输出流量为：

式中：QL为负载流量，m3s；KQ为滑阀的流量增益；KC为滑阀的流量-压力放大系数；xv为滑阀阀芯相对中立位置的位移，m；pl为负载压差，N m2；ps为系统供油压力，N m2；Cd为控制窗口处的流量系数；ρ为油液密度，Kg/m3；W为滑阀的面积梯度（开口周边总长），m.

1.2 传递函数的简化

电液伺服阀是液压控制系统的核心元件，其压力-流量特性是非线性的。伺服阀通常以电流Δi为输入参量，以空载流量Q0=KQxv作输出流量。在大多数电液伺服系统中，伺服阀的动态响应往往高于动力元件的动态响应[2]。为了简化系统传递函数，一般用二阶振荡环节来表示，此时伺服阀的传递函数可表示为：

式中：ωsv为伺服阀固有频率，伺服阀的频宽通常以幅值比为-3 dB时所对应的频率作为幅频宽，以相位滞后90°时对应的频率作为相频宽，可根据控制的需要选取；ζsv为伺服阀的阻尼比；Ksv为伺服阀的流量增益。

可以根据二阶环节的相频特性公式：

由频率特性曲线求出每一相角ϕ所对应的ζsv值，然后取平均值。

一般情况下，伺服阀二阶环节的固有频率高于动力元件的固有频率，伺服阀的传递函数还可用一阶惯性环节表示，当伺服阀的固有频率远大于动力元件的固有频率，伺服阀可看成比例环节。一阶惯性环节可由下面公式估计：

式中：ωsv为伺服阀转折频率，一般取频率特性曲线上相位滞后45°时对应的频率。

2 传递函数模型建立

阀控液压缸的动态特性取决于阀和液压缸的特性，并和负载有关，描述动力元件的微分方程是非线性的。假定：阀与液压缸的连接管道对称且短而粗，管中压力损失和管道动态可以忽略；液压缸每个工作腔内各处压力相等[3]，油温和体积弹性模量为常数；液压缸内、外泄露均为层流流动。

根据流量的连续性，可写出液压缸工作腔的流量方程为:

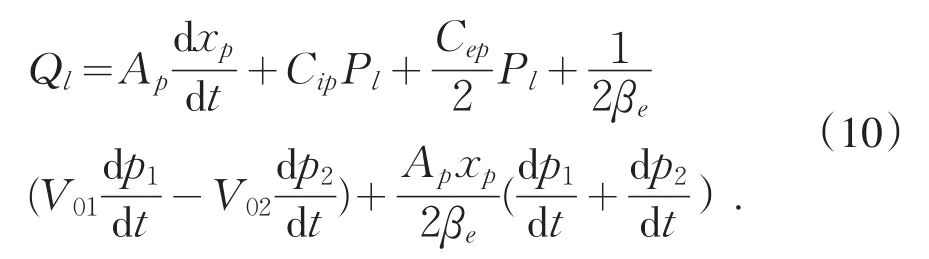
式中:Ap为液压缸活塞面积，m2；Cip为液压缸内泄漏系数，m5/N⋅s；Cep为液压缸外泄漏系数，m5/N⋅s；βe为有效体积弹性模量，N m2；xp为液压缸活塞位移，m；V01为进油腔的初始容积，m3；V02为回油腔的初始容积，m3；p1为进油腔的压力，N m2；p2为回油腔的压力，N m2。

液压缸总压缩容积为Vt，V0是活塞在中间位置时每一个工作腔的容积。由于Apxp＆lt;＆lt;V0，则上式可简化为：

Ctp为液压缸总泄漏系数为推动液压缸活塞运动所需的流量，CtpPl为总泄漏流量，为总压缩流量。

若忽略库仑摩擦等非线性负载，则可以得到液压缸的负载力平衡方程为：

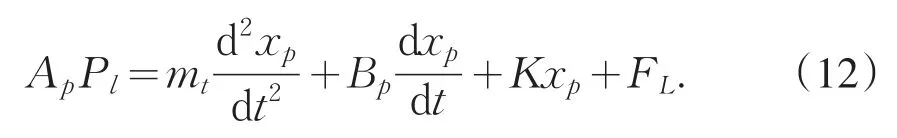
式中：mt为活塞及负载折算到活塞上的总质量，kg；Bp为活塞及负载的粘性阻尼系数，N⋅s/m；K为负载弹簧刚度，N m；FL为作用在活塞上的任意外负载力，N。

对阀控缸的三个基本方程进行拉氏变换得到：

将上述三式消去中间变量QL与 pl，并将伺服阀可以近似看成比例环节，则有传递函数为：

式中：ωh为液压固有频率，为液压阻尼比，为系统开环增益，Kv为控制器增益，Ksv为伺服阀增益，KQ为流量增益。

3 结束语

详细阐述了电液位置伺服理论的基本概念和基本问题，建立了电液位置伺服系统的各个组件的数学模型，进而建立位置了电液伺服系统的理论模型；然后推导电液位置伺服系统的液压缸和伺服阀及其他环节的的参数，分别确定了各个组件的传递函数，最终确定了系统的传递函数。

[1] 王春行.液压伺服控制系统[M]．北京：机械工业出版社，1982．

[2] 王占林.近代电气液压伺服控制[M]．北京：北京航空航天大学出版社，2005．

[3] 江玲玲,张俊俊.基于AMESim与Matlab/Simulink联合仿真技术的接口与应用研究[J]．机床与液压，2008(1)：148-149.