一种新的低/零碰撞区跳频序列集构造方法*

2013-06-24薛国红裴少婷李明阳

电讯技术 2013年12期

关键词：跳频构造方法交织

邬蒙,薛国红,裴少婷,李明阳

(1.空军工程大学航空航天工程学院,西安710038;2.空军装备部,北京100843; 3.空军工程大学综合电子信息系统与电子对抗技术研究中心,西安710051)

一种新的低/零碰撞区跳频序列集构造方法*

邬蒙1,**,薛国红2,裴少婷1,李明阳3

(1.空军工程大学航空航天工程学院,西安710038;2.空军装备部,北京100843; 3.空军工程大学综合电子信息系统与电子对抗技术研究中心,西安710051)

低/零碰撞区跳频序列能够应用于准同步跳频通信系统中以缓解多址干扰的影响。提出了一种新的基于交织方法的低/零碰撞区跳频序列集构造方法。针对序列集的不同参数设计合理的移位序列,通过交织变换构造具有最优或次优性的低/零碰撞区跳频序列集。对不同参数进行了数值仿真,得到和所提方法一致的结论,且该方法构造的序列集具有更低的周期碰撞次数,实用性更强。新的低/零碰撞区跳频序列集可以应用于准同步跳频通信系统中,从而获得更优的性能。

准同步跳频通信系统;码分多址;低/零碰撞区;交织变换;移位序列;最优或次优

1 引言

跳频通信系统具有抗干扰、抗多址的能力,已经在军用和民用通信领域得到广泛应用[1]。跳频序列的性能对跳频系统影响很大,设计具有良好性能的跳频序列一直是跳频通信研究的重要内容[2]。基于有限域理论,文献[3]研究了利用迹函数和d-型函数构造最优跳频序列的方法,该方法没有考虑序列集的构造,应用范围较窄。目前低/零碰撞区(Low Hit Zone/No Hit Zone,LHZ/NHZ)跳频序列集的构造主要包括交织方法[4-5]和基于代数理论[6]的构造方法。文献[5]利用最优跳频序列基于迭代交织方法构造新的跳频序列集,但该方法对原序列有较大限制,缺乏灵活性。文献[7-9]构造了最优或近似最优的LHZ跳频序列,但该方法同样只能构造跳频序列。文献[10]对具有最优部分Hamming相关函数的跳频序列进行了研究,但部分Hamming相关函数不能完全表征跳频序列的碰撞性能。文献[11]构造了具有三NHZ的跳频序列集,多NHZ序列集能够充分利用跳频频隙但是需要相应的较为复杂的通信协议。文献[12]研究了具有较低平均汉明相关函数的跳频序列集,并证明任何具有一致分布的跳频序列都具有平均最优性,但是低平均相关性并不能保证低碰撞区内获得更好的效果。文献[13]利用笛卡尔积和交织方法构造了最优和准最优LHZ跳频序列集,且该方法获得的序列集数量较多,但是文中没有给出基于交织的具有一般性的构造方法。文献[4,14]基于交织法获得较大容量的LHZ跳频序列集,但是序列集的Hamming相关函数在序列周期内碰撞点较多。

本文提出一种基于交织变换的LHZ/NHZ跳频序列集构造方法。首先根据交织变换后新序列集Hamming相关函数的性质分析了新的Hamming相关值在某个区域内保持较低值时移位序列必须满足的条件,然后该方法针对序列集的不同参数设计了两种不同的移位序列。文中证明当采用这两种移位序列时,构造的LHZ/NHZ跳频序列集的参数具有最优性或次优性,且不要求最优性时该方法能够获得更灵活参数的LHZ/NHZ跳频序列集。最后通过3个仿真实例证明该方法的有效性,且本文方法相对于已有方法在非低/零碰撞区能够获得更低的碰撞次数,性能更优。

2 基本定义

设频隙数为q的频隙集F={f0,f1,…,fq-1},对于任意fi,fj∈F,令

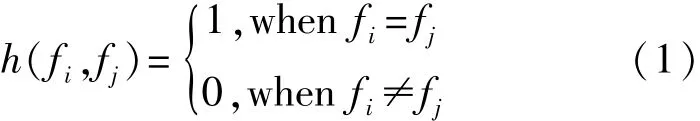
定义1 在频隙集F上存在两个长度为L的跳频序列x={x0,x1,…,xL-1},y={y0,y1,…,yL-1},相对时延为t的Hamming相关函数定义为

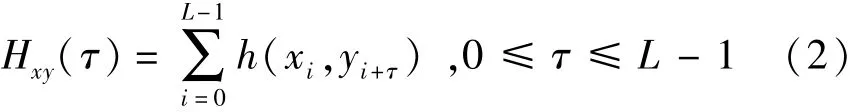
其中,i+t按模L-1计算。特别地,当x=y时称其为Hamming自相关函数,当x≠y时称其为x和y的Hamming互相关函数。

定义2 频隙集F上一个长度为L的跳频序列x={x0,x1,…,xL-1},其Hamming自相关函数满足

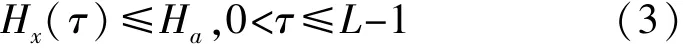
则称序列x为q频隙上长度为L、最大自相关函数为Ha的跳频序列,表示为FHS(L,q,Ha)。

定义3 设频隙集F上一M维跳频序列集C= (c0,c1,…,cM-1),其中ci=(ai0,ai1,…,aiL-1)。设i,j∈[0,1,…,M-1],序列集C中任意两序列在一定时延范围内的Hamming相关函数Hcicj(τ)≤Hm,这个范围的最小值定义为低碰撞区,表示为

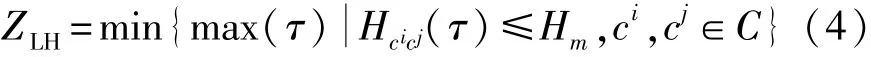
序列集C称为低碰撞区跳频序列集,表示为LHZ(q,L,M,ZLH,Hm)。当Hm=0时,低碰撞区又称为零碰撞区,表示为ZNH,相应的序列集C又称为零碰撞区跳频序列集,表示为NHZ(q,L,M,ZNH)。

3 低/零碰撞区跳频序列集构造方法

设跳频序列a=(a0,a1,…,aL-1)为FHS(L,q, Ha),e=(e0,e1,…,eN-1)为长为N的移位序列。根据a和e构造一个矩阵U:

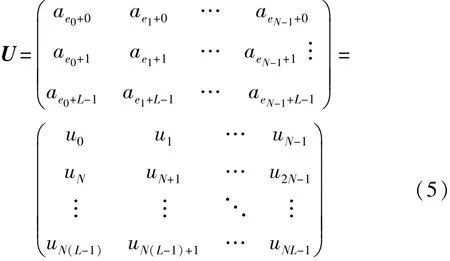
定义交织序列u=(u0,u1,…,uNL-1),满足u= I(Lea))=I(Le0(a),Le1(a),…,LeN-1(a)),其中Li(x)表示对序列x的i位循环左移,I(X)表示对矩阵X进行交织。同理根据a和另一移位序列f= (f0,f1,…,fN-1)构造另一个交织序列v=(v0,v1,…, vNL-1)=I(Lf0(a),Lf1(a),…,LfN-1(a))。设τ=Nτ1+ τ2,序列u和序列v的Hamming相关函数可以用序列a的Hamming自相关函数表示[4],满足式(6)。

设

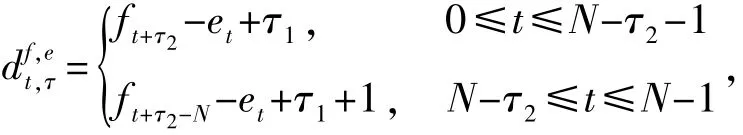
根据式(6)易知当移位序列集满足条件1时基于交织方法能够构造低相关区为ZLH,低相关值为NHa的LHZ跳频序列集。

条件1 假设存在0＜ZLH≤L,当e≜f且0＜τ≤ZLH时或e≠f且0≤τ≤ZLH时,满足≠0。

设跳频序列a=(a0,a1,…,aL-1)为FHS(L,q, Ha),移位序列集e={eii∈[0,1,…,M-1]},其中为长为N的移位序列,当满足定理1、定理2时交织序列集S=为LHZ/NHZ跳频序列集。

证明当gcd(N,L)=1时,易知当0≤t≤N-τ2-1时;当N-τ2≤t≤N-1时综合可得

证毕。

证明当L|N时,易知当0≤t≤N-τ2-1时(i-k)N+τ2+τ1;因为,所以当N-τ2≤t≤N-1时(i-k)N+τ2+τ1+1。且当0＜τ≤N-2时,可知τ1=0,τ2=τ。

当ei≜ek且0＜τ≤N-2时,=,可知当移位序列ei≠ek,且延迟0＜τ≤N-2时,0＜dei,ekt,τ≤(M-1)N+N-2+1＜MN=L。根据条件1可知序列集S为LHZ (LN,q,M,N-2,NHa),特别的当原序列为NHZ序列时,序列集S为NHZ(qN,q,M,N-2)。

证毕。

当L|N时,根据以上证明过程可以得到更一般的结论,设移位序列=(i(ZLH+2)+j)mod q,则序列集S为LHZ(LN,q,M,ZLH,NHm)。其中,0＜ZLH≤N-2。

文献[15]给出了LHZ和NHZ跳频序列集的理论界,满足式(8)和式(9)。

当gcd(L,N)=1时,序列集S的参数满足

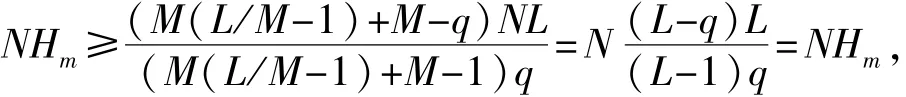
达到下界,为最优低碰撞区跳频序列集。当L|N时,序列集S的参数满足

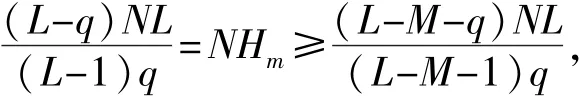
可见序列集的低碰撞区距离最优仅相差1,为次优LHZ跳频序列集。

当gcd(L,N)=1时,根据定理1构造的零碰撞区序列集为NHZ(qN,q,M,q/M-1),此时式(9)左右两边取等号,也即序列集参数达到理论界,为最优NHZ序列集。当L|N时,将构造的序列集的参数代入式(9)得到」,所以该方法构造的序列集不具有最优性,但ZNH距离最优仅相差1,所以此时序列集为次优NHZ跳频序列集。当利用定理2构造更一般的情况时,序列集不具有最优或次优性,但是构造的序列集参数更灵活。

4 数值仿真

仿真q|N的情况,选取NHZ序列a=(0,1,2, 3,4,5,6,7,8,9,10,11,12,13,14,15),其余参数如表1所示。

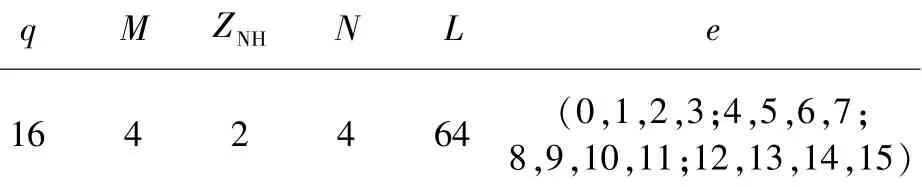
表1 q|N时的仿真参数Table 1 Simulation parameters when q|N

根据定理2构造序列集S=(si|i∈[0,1,2, 3]),其中:

其Hamming相关函数为

其部分相关函数如图1所示。

图1 本文构造的零碰撞区序列集相关函数Fig.1 Correlation function of the NHZ sequence set constructed in this paper

由图1可知,零碰撞区为2=N-2,和定理2结论一致,此时可以构造次优低/零碰撞区跳频序列集。

仿真gcd(q,N)=1的情况,选取LHZ序列a= (1,1,0,1,6,2,4,5,6,6,0,6,1,5,3,2),其余仿真参数如表2所示。

表2 gcd(q,N)=1时的仿真参数Table 1 Simulation parameters when gcd(q,N)=1

根据定理1构造序列集S=(si|i∈[0,1,2, 3]),其中:

其Hamming相关函数为

其中,x(y)表示连续y个x。其部分相关函数如图2所示。

图2 本文构造的低碰撞区序列集相关函数Fig.1 Correlation function of the LHZ sequence set constructed in this paper

由图2可知,序列集的零碰撞区为3=L/M-1,和定理1结论一致,此时可以构造最优NHZ跳频序列集。同时由图2可以直观地看出,本文方法构造的NHZ序列集具有均匀分布的零碰撞区,在QSCDMA跳频通信系统中可以利用合理的通信协议[11]对这些零碰撞区加以利用。

选取a=(0,1,2,3,4,5,6,7,8,9,10,11,12,13, 14,15),其余参数同表2。根据定理1构造序列集S={si|i=[0,1,2,3]},其中:

序列集的汉明相关函数为

参数不变,利用文献[14]方法构造NHZ跳频序列集,两种方法构造的序列集的部分相关函数如图3所示。

图3 该方法和文献[14]方法构造的序列集的部分相关函数Fig.1 Comparison of part correlation function of the sequence set constructed in this paper and reference[14]

由图3可以看出,两种方法构造的序列集的零碰撞区都为3=L/M-1,即两者都可以构造最优NHZ跳频序列集。然而一周期内文献[14]方法碰撞9次而本文方法周期碰撞次数为5次,本文方法构造的序列集周期碰撞次数更少。

5 结束语

本文提出了一种基于交织变换的低/零碰撞区跳频序列集构造方法,该方法针对原序列长度与移位序列长度互素和原序列长度是移位序列长度整数倍两种情况分别给出不同的移位序列。当选择的频隙长度和移位序列长度互素时该方法可构造最优低/零碰撞区跳频序列集,当频隙长度是移位序列长度的整数倍时,可以构造次优低/零碰撞区跳频序列集。且在不要求最优性时,该方法可以根据低/零碰撞区的长度构造具有灵活参数的调频序列集。该方法构造的序列集具有较为规律的低/碰撞区分布,相对于已有方法具有更少的周期碰撞次数,因而可以降低跳频通信协议复杂度,具有更高的实用性。已有的研究都是基于无符号交织,有符号交织有望获得新的更优的跳频序列集。

[1] Zeng Q,Peng D Y,Wang X N.Performance of a Novel NFSK/FHMA system employing no-hit zone sequence set over rayleigh fading channel[J].IEICE Transactions on Communications,2011,E94-B(2):526-532.

[2] Zeng Q,Li H,Peng D Y.Frequency-Hopping Based Communication Network With Multi-Level QoSs in Smart Grid:Code Design and Performance Analysis[J].IEEE Transactions on Smart Grid,2012,3(4):1841-1852.

[3] 刘方,彭代渊,范平志,等.一类具有最优汉明自相关特性的跳频序列[J].电子学报,2013,41(1):13-17. LIU Fang,PENG Dai-yuan,FAN Ping-zhi,et al.A new class of frequency-hopping sequences with optimal Hamming autocorrelation[J].Acta Electronica Sinica,2013, 41(1):13-17.(in Chinese)

[4] Niu X H,Peng D Y,Zhou Z C.New classes of optimal low hit zone frequency hopping sequences with new parameters by interleaving techinique[J].IEICE Transactions on Fundametals of Electroincs,Communications and Computer Science,2012,E95-A(11):1835-1842.

[5] Zeng X Y,Cai H,Tang X H,et al.A class of optimal frequency hopping sequences with new parameters[J]. IEEE Transactions on Information Theory,2012,58(7): 4899-4907.

[6] Chung J H,Yang K.K-fold cyclotomy and its application to frequency-hopping sequences[J].IEEE Transactions on Information Theory,2011,57(4):2306-2317.

[7] Ma W P,Sun S H.New designs of frequency hopping sequences with low hit zone[J].Designs,Codes and Crytography,2011,60(2):145-153.

[8] Chung J H,Han Y K,Yangk Y.No-hit zone frequencyhopping sequence sets with optimal Hamming autocorrelation[J].IEICE Transactions on Fundamental of Electronics,Communications and Computer,2010,E93-A(11): 2239-2244.

[9] Chung J H,Yang K.Optimal frequency-hopping sequences with new parameters[J].IEEE Transactions on Information Theory,2010,56(4):1685-1693.

[10] Zhou Z C,Tang X H,Niu X H,et al.New classes of frequency-hopping sequences with optimal partial correlation[J].IEEE Transactions on Information Theory, 2012,58(1):453-458.

[11] Jiang X Y,Zhang C,Lu J H.Time-frequency hopping sequences with three no hit zones[J].Wireless Network,2009,15(1):455-461.

[12] Chung J H Y K.New frequency-hopping sequence sets with optimal average and good maximum Hamming correlations[J].IET Communications,2012,6(13):2048-2053.

[13] Chung J H,Yang K.New classes of optimal low-hitzone frequency-hopping sequence sets by Cartesian product[J].IEEE Transactions on Information Theory, 2013,59(1):726-732.

[14] Niu X H,Peng D Y,Zhou Z C.New classes of optimal frequency hopping sequences with low hit zone with new parameters[C]//ProceedingsofFifthInternational Workshop on Signal Design and its Applications in Communications.Guilin:IEEE,2011:111-114.

[15] Fan P Z,Peng D Y,Suehiro N.Theoretical bound onno hit zone of frequency hopping sequences[C]//Proceedings of Fifth International Workshop on Signal Design and its Applications in Communications.Guilin: IEEE,2011:115-117.

WU Meng was born in Xi′an,Shaanxi Province,in 1978.He received the M.S.degree from Air Force Engineering University in 2005.He is now a lecturer.His research concerns signal and information processing.

Email:wu316wu@21cn.com

薛国红(1983—),男,山西万荣人,2009年于空军工程大学获硕士学位,现为工程师,主要研究方向为装备管理;

XUE Guo-hong was born in Wanrong,Shanxi Province,in 1983.He received the M.S.degree from Air Force Engineering University in 2009.He is now an engineer.His research concerns equipment management.

裴少婷(1986—),女,山西长治人,2013年于空军工程大学获硕士学位,现为讲师,主要研究方向为计算机科学;

PEI Shao-ting was born in Changzhi,Shanxi Province,in 1986.She received the M.S.degree from Air Force Engineering University in 2013.She is now a lecturer.Her research concerns computer science.

李明阳(1985—),男,河北保定人,2010年于空军工程大学获硕士学位,现为博士研究生,主要研究方向为扩频通信。

LI Ming-yang was born in Baoding,Hebei Province,in 1985.He received the M.S.degree from Air Force Engineering University in 2010.He is currently working toward the Ph.D. degree.His research concerns spread spectrum communication.

A Novel Construction Method of Low/No-Hit Zone Frequency
Hopping Sequence Set Based on Interleaving Technique

WU Meng1,XUE Guo-hong2,PEI Shao-ting1,LI Ming-yang3

(1.Aeronautics and Astronautics Engineering College,Air Force Engineering University,Xi′an 710038,China; 2.Air Force Equipment Ministry,Beijing 100843,China;3.Synthetic Electronic Information System and Electronic Countermeasure Technology Research Department,Air Force Engineering University,Xi′an 710051,China)

Low/no-hit zone(LHZ/NHZ)frequency hopping(FH)sequence set can be used in quasi-synchronous code division multiple access(QS-CDMA)FH communication system to eliminate multiple access interference.In this paper,a novel construction method of LHZ/NHZ FH sequence set based on interleaving technique is derived.Optimal or sub-optimal LHZ/NHZ FH sets are constructed through interleaving transformation when shift sequences are rationally designed for variable parameters of the sequence sets.Numerical simulations for different parameters are consistent to the construction method,besides,the sequence set constructed by it has less periodical collisions and higher practicality.The novel LHZ/NHZ sequence sets can be employed in QS-CDMA FH communication systems to achieve better performance.

quasi-synchronous FH communication system;CDMA;low/no-hit zone(LHZ/NHZ);interleaving transformation;shift sequence;optimal or sub-optimal

The National Natural Science Foundation of China(No.61174194)

date:2013-04-09;Revised date:2013-11-19

国家自然科学基金资助项目(61174194)

**通讯作者:wu316wu@21cn.com Corresponding author:wu316wu@21cn.com

TN911.22

:1001-893X(2013)12-1586-06