基于粒子群优化算法的寻源导热反问题研究
2013-06-23李博汉
张 涛, 卢 玫, 陶 亮, 李博汉
(上海理工大学能源与动力工程学院,上海 200093)
基于粒子群优化算法的寻源导热反问题研究
张 涛, 卢 玫, 陶 亮, 李博汉
(上海理工大学能源与动力工程学院,上海 200093)
给出了描述导热问题的数学模型,根据最小二乘法原理建立导热反问题的目标函数,并采用从鸟群捕食行为演化而来的粒子群优化算法对含有热源项的导热反问题进行热源位置的反演求解,同时对粒子群优化算法中惯性系数的取值范围进行了讨论.结果表明:采用粒子群算法反演热源的位置可以取得较好的结果,使用随迭代次数变化的惯性系数可以加快算法的收敛速度.
热传导;反问题;热源;粒子群优化算法
寻源导热反问题是指利用已知研究对象边界上或内部若干测点的温度,反演求解热源位置或热源强度.在生物医学、航空航天、化工制药、热工测量、无损探伤、电子散热等领域都会涉及到此类反问题,如探寻电脑芯片中大量热产生的热源问题、微波炉的传热过程、化学反应过程如何确定反应产热的热源问题等[1].反问题一般具有不适定性,较小的测量误差就可能导致问题多解或者无解,因此导热反问题成为许多学者的研究重点.导热反问题的研究主要有热物性参数的识别[2]、边界形状的识别[3]、边界条件的识别[4]以及对各种反演算法的研究等.关于热源项的反演研究相对比较少.Huang等[5]利用共轭梯度法反演热源强度大小,Silva等[6]用同样方法研究了两个热源的强度反演问题.早期求解导热反问题的算法主要有正则化法、共轭梯度法、高斯牛顿法等.Huang[7]采用共轭梯度法识别二维一阶非定常导热问题的不规则几何形状,指出了共轭梯度法抗噪性能较好,但收敛速度较慢;杨海天等[8]采用高斯牛顿法对非线性导热反问题进行了求解.近年来随着计算机技术和仿生学的发展,一些学者将遗传算法、神经网络法、蚁群算法等引入导热反问题领域,取得了很好的结果,丰富了导热反问题的求解方法.粒子群优化算法(PSO)是由美国的Kenney和Eberhart[9]在1995年提出的,该算法是以粒子对群体中最优粒子的追随进行解空间的搜索.PSO的优点在于程序流程简单易实现、算法参数少易调整、收敛速度快、且有很多措施可以避免陷入局部最优.因此PSO从出现后,很快应用到函数优化、模糊控制等领域.
1 含内热源的二维稳态导热问题数学模型

式中,λ为导热系数,W/(m·K);T为温度,K;Φ为点热源强度,W,其对应的热源位置为(xΦ,yΦ);Г为求解物体的边界,Г=Г1+Г2+Г3为第一类边界条件温度分布,K;q为第二类边界条件的热流密度,(W/m2);h为第三类边界条件的表面对流换热系数,W/(m2·K);Tw,Tf分别为壁面温度和外界流体的温度,K.
2 反演模型及粒子群优化算法
2.1 反演模型
对于反演热源位置的导热反问题,其热源位置的确定必须附加物体表面或者内部测点的测量信息来确定.其求解可以归结为优化问题

式中,N为温度测点数目;T0(x,y)为边界测点的实测温度;Tc(x,y)为反演的热源位置代入方程式(1)、边界条件式(2)求得的对应测点的计算值.目标函数J随反演过程中搜寻的热源位置(xi,yj)而变化,当(xi,yj)趋于真实热源位置(xΦ,yΦ)时,式(3)所示目标函数就趋于最小值,此时热源位置(xi,yj)即为反演所求结果.
2.2 粒子群优化算法
PSO来源于对鸟群搜寻食物的行为研究.鸟群在一个区域内随机搜索食物源时,所有鸟都不知道食物源在哪里,但是它们知道当前离食物源最近的鸟在哪里,所以找到食物最好的策略就是搜寻目前离食物源最近鸟的周围区域.PSO即是从这种模型中得到启示并用于解决优化问题.在PSO中,搜寻食物的鸟被称为“粒子”.粒子飞行到一个位置后都有一个描述该位置距离食物源远近的适应值,并且会根据最优粒子的位置调整飞行到下一位置的速度矢量,以此追随当前的最优粒子在解的空间中搜索.如在一个D维区域内,由m个粒子构成一个群体.设zi=(zi1,zi2,…,ziD)为第i个粒子(i=1,2,…,m)飞行到某一位置的空间坐标,根据事先设定的目标函数计算zi当前的适应值,以衡量粒子所在位置的优劣;vi=(vi1,vi2,…,vid,…,viD)为粒子i的下一次的飞行速度,即粒子下一次的飞行距离和方向;每个粒子迄今为止找到的最优位置为pbi=(pi1,pi2,…,pid,…,piD);整个群体迄今为止找到的最优解位置为gb=(g1,g2,…,gd,…,gD).
对于所要研究的寻源导热反问题,热源位置等同于鸟群捕食的食物源;导热区域为搜索热源的空间范围;式(3)所示目标函数值的大小表示鸟离食物源的距离.某个粒子当前已飞过的所有位置中,对应目标函数最小的那个位置为该粒子的个体极值,即pbi;整个粒子群所找到的对应目标函数最小的位置为全局极值,即gb.粒子通过更新方程改变每次搜寻的速度,进行下一次迭代(即飞行).
PSO的粒子速度更新方程为

式中,k为当前的迭代代数;c1,c2为学习因子;r1,r2为[0,1]范围内的随机数.迭代终止条件设为最大迭代次数或者搜索到满足精度要求的最优解.所示PSO速度更新方程中,等号右边由三项组成:第一项表示粒子当前的速度,第二项是根据粒子本身的个体极值对速度的调整,第三项是根据粒子群的全局极值对速度的调整.
在基本PSO的基础上,通过添加惯性系数ω来调整粒子当前速度对下一次飞行速度的影响程度.粒子速度更新方程为

其中,ω的取值可以为常数,亦可根据迭代次数的增加而减小,即计算式为

式中,ωmax,ωmin为最大和最小惯性系数;k,kmax为当前迭代次数和最大迭代次数.
2.3 寻源反演过程
图1所示,为所编制的采用PSO算法反演热源位置的导热反问题流程框图.

图1 PSO算法求解导热反问题流程图Fig.1 Flow chart of solving IHCP by PSO
具体实现步骤如下:
Step1 初始化粒子群,在搜索空间内随机给定粒子的初始位置(xi,yi)和初始速度vi;
Step2 根据粒子的位置代入导热正问题,求出测点位置的计算温度值,代入目标函数求其适应值;
Step3 根据各粒子的适应值,更新粒子的个体极值pbi、和全局极值gb;
Step4 根据式(5)-(7)更新各粒子的速度和位置;
Step5 判断g是否满足设定的要求,满足则计算结束;不满足进行下一步;
Step6 判断迭代次数是否达到设定的最大值,若是,则迭代结束,否则,转到step2.
3 计算结果及分析
采用上述方法,对含有内热源二维稳态导热反问题进行了反演计算.反问题物理模型为一个截面形状为正方形的二维导热物体,边长为0.1 m,截面上有一个强度为Φ的点热源,热源位置未知,如图2所示.
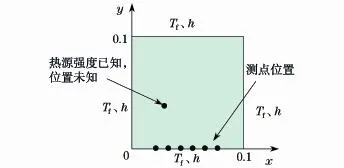
图2 二维带点热源导热反问题示意图Fig.2 Sketch map of 2-D IHCP with point heat source
热源位置反演模型的数学描述为式(1),边界条件为

其中,外界流体温度tf=24℃,对流换热系数h= 13 W/(m2·K),导热系数λ=1.5 W/(m·K).边界上选取6个测点温度,并根据导热正问题模型计算求得.计算中取点热源强度Φ=72 W,热源位置为(0.039 5,0.029 5).表1给出了对应测点的温度值.

计算中PSO算法参数设置为粒子规模m= 20,速度v=(v1,v2)中v1、v2∈[-0.03,0.03],zmin=0,zmax=0.1,取c1=1.5、c2=2.5[10],设置最大迭代次数为20次.首先取ω为定值进行计算,ω取值分别为0.0,0.1,0.2,…,1.0;然后再按式(7)取ω进行对比计算.为了避免搜索结果的偶然性,每个工况计算10次,然后对计算结果取其平均值.采用数值模拟方法进行计算,计算结果如表2所示.

表2 计算结果Tab.2 Results of calculation
从表2所列数据可以看出,在0~1范围内,不论惯性系数ω取何值,粒子群算法最终几乎都能找到热源位置,但对搜索速度有影响.当ω=0时,式(6)第一项为零,则速度自身无记忆性,粒子飞行速度仅由自身当前位置、个体最优位置和群体最好位置决定,计算结果表明,其平均迭代次数基本达到最大;当ω过大时,粒子原有的速度起较大的作用,也就不断向新的区域探索,这时粒子需要更多的迭代才能搜寻到热源位置.
从表2数据可以看出,ω取为定值,其取值范围在0.3~0.7时搜索速度比较快.表2最后一行数据为ω按式(7)计算结果,式(7)中,取ωmax=0.9,ωmin=0.3,ωmax选择大于0.7,目的是为了使粒子在搜索前期偏向于全局搜索.计算结果表明,取随迭代次数变化的ω可以加快粒子群算法的收敛速度.
反演过程中,每个粒子飞行到一个位置,就要进行一次导热正问题的计算,以计算目标函数.图3所示为反演过程中目标函数随正问题计算次数tm变化曲线.可以看出,导热计算区域网格划分为100× 100时,正问题计算次数不足200次就能找到导热区域中的热源位置.图4所示为初始时刻粒子群在求解区域内的位置分布,图5所示分别为第二次、第四次、第六次和第八次迭代时刻粒子群的位置分布.可以看出,粒子群中的每个粒子每次迭代后根据式(6)调整飞行速度的方向和大小,从而使粒子群从初始的随机分布逐渐趋于集中,最终逼近热源位置,目标函数达到最小.

图3 目标函数随正问题计算次数的变化Fig.3 Objective function variation with time

图4 初始粒子群的分布Fig.4 Distribution of particles at the beginning

图5 迭代过程中粒子的分布Fig.5 Distribution of particles during the process of iterations
4 结 论
采用粒子群优化算法,建立了适合于寻源导热反问题的求解方法,并对粒子群算法中惯性系数ω的取值范围进行讨论.ω设为定值时,其取值范围在0.3~0.7能取得较好的求解结果;ω采用式(7)计算时,设ωmax=0.9、ωmin=0.3,可以在满足全局最优的同时,加快收敛的速度.数值计算结果表明,在参数设置合适时,利用粒子群优化算法反演导热区域的热源位置具有较高的精度和较好的稳定性.
[1] Yang CY.The determination of two moving heat sources in two-dimensional inverse heat problem[J].Applied Mathematical Modelling,2005,30(3):278-292.
[2] Beck J V,Blackwell B,Haji-Sheikh A.Comparison of inverse heat conduction methods using experimental data[J].International Journal of Heat Mass Transfer,1996,39(17):3649-3657.
[3] Huang C H,Chao B H.An inverse geometry problem in identifying irregular boundary configurations[J]. International Journal of Heat and Mass Transfer, 1997,40:2045-2053.
[4] Refahi Abou khachfe,Yvon Jarny.Determination of heat sources and heat transfer coefficient for twodimensional heat floe-numerical and experimental study[J].International Journal of Heat and Mass Transfer,2001,4:1309-1322.
[5] Huang C H,Ozisik M N.Inverse problem of determining the unknown strength of an internal plate heat source[J].Franklin Inst,1992,329:751-764.
[6] Silva Neto A J,Ozisik M N.Inverse problem of simultaneously estimating the time-varying strengths of two plane heat sources[J].Appl Phys,1993,73(5):2132-2137.
[7] Huang C H.Transient inverse two-dimensional geometry problem in estimating time-dependent irregular boundary configurations[J].International Journal of Heat and Mass Transfer,1998,41(12):1707 -1718.
[8] 杨海天,薛齐文.两级敏度分析求解非线性稳态多宗量热传导问题[J].工程热物理学报,2003,24(3):463 -465.
[9] Kennedy J,Eberhart R.Particle Swarm Optimization[C]//Proceedings of IEEE International Conference on Neural Networks.Perth:IEEE,1995.
[10] 范培蕾,张晓今,杨涛.克服早熟收敛现象的粒子群优化算法[J].计算机应用,2009,29(6):122-124.
(编辑:金 虹)
Seeking Heat Source in Inverse Heat Conduction Problem by Using Particle Swarm Optimization
ZHANGTao, LUMei, TAOLiang, LIBo-han
(School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
A numerical model was built for the solution of heat conduction problems.In solving inverse problems,a least-square based objective function was minimized by PSO.A new robust solving method to determine the heat source in IHCP.was developed.With a number of numerical examples,the evaluation of inertia coefficient in PSO was studied.The results show that the proposed method is an accurate and efficient method to determine the location of heat source in IHCP.
heat conduction;inverse problem;heat source;particle awarm optimization(PSO)
TK 124
A
1007-6735(2013)04-0377-05
2012-12-17
国家自然科学基金资助项目(51176126)
张 涛(1987-),男,硕士研究生.研究方向:导热反问题.E-mail:zhangtaobeyond@126.com
卢 玫(1958-),女,教授.研究方向:强化传热和能量有效利用.E-mail:rose_luu@usst.edu.cn
