经济动态系统的一种几何描述框架
——Lagrange体系模型
2013-06-23周石鹏
周石鹏
(上海理工大学管理学院,上海 200093)
经济动态系统的一种几何描述框架
——Lagrange体系模型
周石鹏
(上海理工大学管理学院,上海 200093)
为方便地将物理学中的对称性分析方法应用到经济动态系统的研究中,从而揭示经济系统所内蕴的特性及其运行规律,给出了一种以Lagrange体系模型形式将主流经济学中的大多数经济动态模型纳入到统一的描述框架中,建立了所谓的经济Vakonomic模型.这种描述框架的特点是:经济动态系统被赋予了一种几何结构,其中应用了微分流形和辛结构的数学方法,同时揭示了经济动态系统与物理系统之间具有某种相似性.
经济动态系统;变分法;微分流形;Vakonomic模型
经济系统的动态行为是当今经济学研究的重要对象.第一个采用分析力学的描述方式来研究经济动态过程中的守恒量是著名的经济学家Samuelson,他在1970年发现了von Neumann型经济增长模型的守恒量并且给出了经济解释[1].之后由Sato推广了该方法,他采用Lie群的方法来寻求更普遍的经济系统之中的对称性与相应的守恒量[2],其研究范围基本上也局限于经济增长方面.本文的目的是要推广这种研究方法,赋予大多数经济动态系统以一种统一的几何描述框架,指出以带约束的变分问题为基础的较普遍的一类Vakonomic模型能自然地应用于描述动态经济系统.同时,也为关于经济系统对称性与守恒量及其规范场建模系列研究的后续文章提供了一个基本的描述框架,这样一种研究视角能使人们更深入地认识经济动态系统的基本规律.
1 动态经济系统的Lagrange体系与Vakonomic模型
1.1 基本术语与记号
一个经济动态系统是由一组随时间t变化的变量{q1(t),q2(t),…,qn(t)}及其时间变化率(导数)来刻画,记q(t)=(q1(t),q2(t),…,qn(t))T∈Rn,则该经济系统的状态就是(q(t),q·(t)).抽象地看,经济系统所处的状态是客观发生的,它们并不因人们所采用的计量单位或统计口径的不同而不同,因此经济系统的所有可能状态的集合应该是一个流形Q的切丛TQ,这里q(t)∈Q,Q被称为经济流形.从局部上看,流形Q上的每点的邻域与欧氏空间Rm同胚(m≤n),即每点的邻域将由一个局部欧氏坐标系(简称局部坐标)来描述,这坐标系可以对应于人们目前所采用的计量单位或统计口径,也可以是另外定义的计量体系或统计口径,当然不同计量体系之间存在连续的变换映射.这样的做法使得对经济系统的刻画摆脱了具体的度量单位和计量方法的束缚,即使得其与坐标系无关,亦即这种方式是对经济系统的内蕴性描述.本文通常要求Q是一个可微流形,也就是说,对于它的任意两个相交的邻域,两个局部坐标之间的变换映射是连续可微的.如果所有的变换都具有k次连续可微性,则称其为k次可微流形.本文约定下面所考察的经济流形均具有问题所需要阶次的可微性.
因为经济系统是由具有寻优行为的主体所组成,由此主流经济学假设经济系统的运行将由某个目标函数的最优化所决定,所以这些系统的动态过程的描述都是归结为一个变分模型或者最优控制模型.这样的经济模型类似于物理学中的Lagrange形式的动力学体系,本文不妨就称它为经济Lagrange体系模型.这种经济Lagrange体系模型可以涵盖很广泛的经济模型,如动态定价模型、生产计划模型、消费函数模型、经济增长模型、资源利用模型等.当前主流的宏观经济理论也是在这种框架下展开的.
1.2 经济Lagrange体系模型
1.2.1 基本模型
假设所考察的经济动态系统的经济空间是流形Q,于是状态空间是切丛,其投影映射记为π:TQ→Q.采用它们的自然局部坐标系,将TQ的元素写成(q,q·),于是π(q,q·)=q.令该经济系统的Lagrange函数为L:TQ→R.那么类似于力学中最小作用量的Hamilton原理,该经济系统在时间[0,T]中的动态路径将由如下泛函的极值所确定,即

其中符号ext表示求极值(极大或者极小).这里泛函的值就是经济系统的目标取值,而经济系统的最优目标值就是该泛函的极值,由此泛函的极值确定了该经济的最优动态路径.
1.2.2 动态方程
假设流形Q上一条连接两个端点q0和qT的可微路径γ:[0,T]→Q是最优路径,考虑连接这两个固定端点的一簇可微曲线cs:[0,T]×(-ε,ε)→Q,它们满足c0(·)=γ(·)和cs(0)=q0,cs(T)=qT,∀s∈(-ε,ε),其中ε是一个充分小的正数.将这些曲线写成是对函数的运算符,而

注意上面给出的是最一般的情形,对端点没有施加任何约束,而对于固定端点的约束条件下有υ=0,故函数W在端点处为零.所以在局部坐标表示下,最优路径γ必然满足Euler-Lagrange方程

这就是决定最优路径的动态方程.
由此可见,Lagrange函数决定了最优路径.但反过来,决定相同路径的Lagrange函数并不是唯一的.事实上,对于任意一个可微函数G:R×Q→R,记它的垂直提升为为投影映射πQ:TQ→Q的拉回映射),即在Q上的每点的切空间上Gv的取值是常量,则容易验证有

因此,两个Lagrange函数L和L′若只相差任意一个时间导数的函数,即, 则它们俩有相同的Euler-Lagrange方程,这函数G被称为该系统的关联函数.
1.3 带约束的经济Vakonomic模型
1.3.1 带约束的经济Lagrange体系模型
前面所讨论的变分问题并不包含约束方程,但是极大多数经济问题都是带约束的.通常,约束条件是由一组定义在TQ上的相互独立的约束方程式所给出,假设它们确定了TQ中的一个子流形M,这个经济的系统的动态路径将由如下带约束的泛函极值来决定:
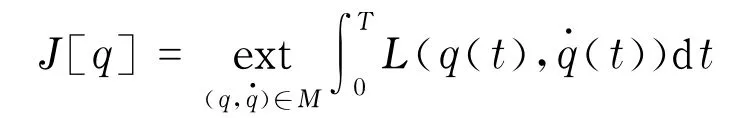
下面将非完整约束力学的Vakonomic处理方式应用于这种带约束的变分模型,并称它为经济的Vakonomic模型.
1.3.2 经济的Vakonomic模型
设在一个n维经济流形Q的切丛TQ上定义一个可微的Lagrange函数L:TQ→R.假设经济系统受到m(m<n)个独立的方程组的约束:

其中函数Φa:TQ→R是可微的且满足
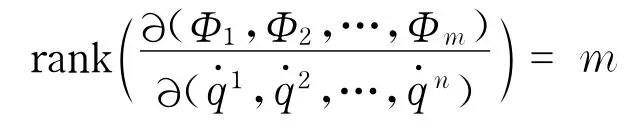
这些约束确定了TQ中的一个(2n-m)维子流形M⊂TQ.于是由隐函数定理可知,这些约束方程可以被显式地写成

其中1≤i≤n,m+1≤k≤n.那么,TQ的子流形M的局部坐标为(qi).
记连接上给定两点q0和qT的二次可微曲线的集合为


定义1(经济的Vakonomic模型) 给定经济流形Q上由一组约束方程所确定的子流形M⊂TQ和一个泛函,则称该泛函约束在流形M上的极值问题为经济的Vakonomic模型(L,M).

Vakonomic模型是应用Lagrange乘数方法处理带约束的变分问题,对此可得出如下结果:
定理1 曲线c是Vakonomic模型(L,M)的解,当且仅当存在m个可微函数(Lagrange乘数)λa:[0,T]→R,0≤a≤m的满足下列方程
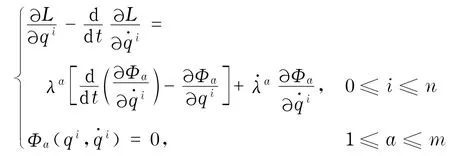
上式和后面均采用Einstein的求和约定.令P≜Q ×Rm,定义增广Lagrange函数=L+:TP→R.于是上面的方程成为对于增广Lagrange函数的Euler-Lagrange方程
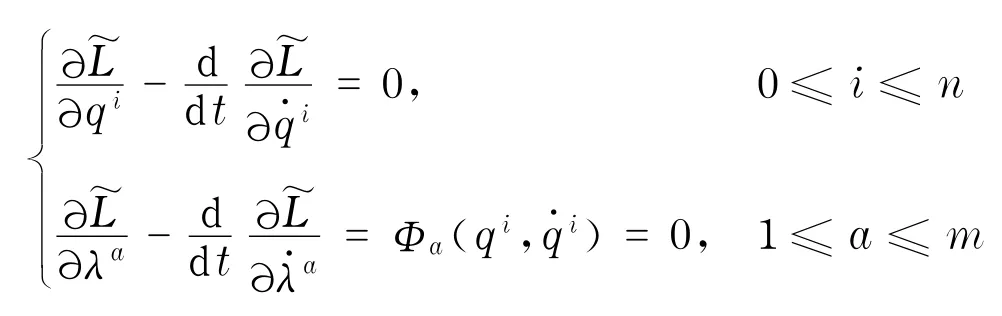
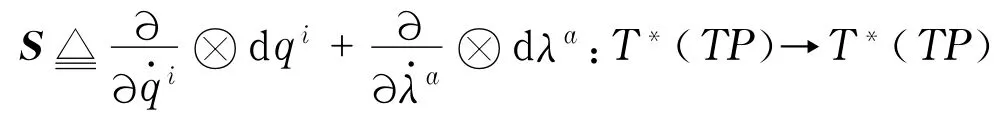
其次,再定义T*(TP)上的张量场:)其中符号⊗表示张量积,由此可得微分1-形式θ= S).
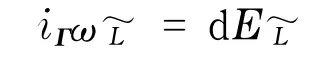
其中iΓ表示内积运算符号,那么上面方程就确定了这个Vakonomic系统的解.但是一般来说,在予辛结构中2-形式并没有像辛流形那样是非退化的,所以该方程并不能在TP上全局地给出解Γ.那么必须对这个予辛结构应用Gotay-Nester算法来产生如下一个子流形序列(详情参见文献[4]):
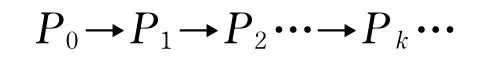
其中令P0=TP,Pk是P0的子流形.这个算法的步骤是:

下面给出两个具体的示例描述.
2 两则示例
现在来考察经济中两个较常见的具体实例.
例1(Taylor模型) 这模型是考察通货膨胀与失业的最优交替变化路径问题.设经济在充分就业下的产出水平为Yf,实际通货膨胀率为π.定义社会损失函数为
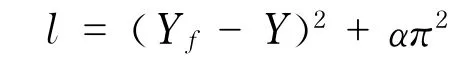
其中α>0是对通胀的权重系数.根据通货膨胀的Phelps关系

其中x表示预期通货膨胀率,假设它由自适应过程决定,即

例2(可枯竭资源的经济增长模型) 这个模型描述经济中可枯竭资源的最优资源配置问题.设K代表可枯竭资源的存量,C代表消费,社会福利由如下效用函数描述为
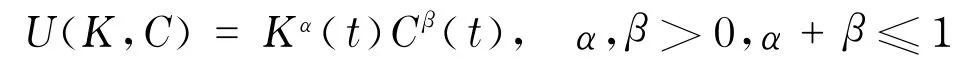

这问题的Lagrange函数为L=Kα(t)Cβ(t),而约束方程为Φ=K·+C=0.令λ为Lagrange乘数,则增广Lagrange函数为=KαCβ+λ(+C).
3 结论
通过上述对经济Lagrange体系模型的研究,可以看到许多经济中的动态系统也与力学一样可以由变分模型来描述,这使得人们可以应用几何力学的方法来更好地研究这些经济动态系统.本文已将动态经济系统统一地纳入到Vakonomic模型形式,并以微分几何的语言来刻画经济动态系统.这样的描述方式不但赋予了经济系统一种几何结构,而且能够让人们看到经济系统与物理系统都拥有某些共同的系统属性.作者将在后续的文章中展示:这样的研究可以方便地将物理学中的对称性分析方法应用到经济动态系统之中,从而使人们更深入地认识经济系统的运行规律.
致谢:作者在此谨向车宏安教授表示由衷的感谢,本项研究受到他的诸多指教与帮助.
[1] Samuelson P A.Law of conservation of the capitaloutput ratio[J].Proceedings of the National Academy of Sciences,Applied Mathematical Science,1970,67(3):1477-1479.
[2] Sato R,Ramachandran R V.Conservation laws and symmetry:applications to economics and finance[M]. Boston:Kluwer Academic Publisher,1990.
[3] Arnold V I.Mathematical methods of classical mechanics[M].2nd ed.New York:Springer-Verlag,1989.
[4] Gotay M J,Nester J M.Presymplectic Lagrangian systems I:the constraint algorithm and the equivalence theorem[J].Ann Inst H PoincaréSect A,1979,30(2):129-142.
(编辑:丁红艺)
A Kind of Geometric Framewor k of Economic Dynamic Systems——Lagrangian Models
ZHOUShi-peng
(Business School,Shanghai University for Science and Technology,Shanghai 200093,China)
The aim of the research is the achievement of conveniently applying the method of physic symmetric analysis in economic dynamic systems in order to uncover characteristics and evolving laws implied in economic dynamic systems.A unified framework which can be well adapted to describe a majority of dynamic economic models in mainstream economics by using the form of a kind of Lagrangian model was presented,and a so-called economic Vakonomic model was built.The feature of this framework is:the dynamic economic systems are endowed with a geometric structure by means of the mathematical method of differential manifold and symplectic structure,meanwhile some analogue between the economic dynamic systems and physic systems was established.
dynamic economic system;variational method;differential manifold;Vakonomic model
N 94;F 019.2
A
1007-6735(2013)04-0321-04
2013-06-10
上海市一流学科(系统科学)建设资助项目(XTKX2012)
周石鹏(1961-),男,副教授.研究方向:数量经济、经济物理和复杂系统.Email:shipengzhou@yeah.net
