基于改进AdaBoost算法的飞机特征图像识别

张 杰，冯巧宁

（中国飞行试验研究院 陕西 西安 710089）

飞行器特征点的计算机智能识别和检测技术是航空试飞领域的关键技术之一。由于飞行器在大气中的飞行速度相对较快，为了保证设备跟踪的准确性，采取基于图像和视频的快速识别算法就显得非常的重要。特征点的识别在早期的研究中主要针对固定模板等具有较强约束条件并且没有形变的特征点图像。图像中特征点的位置较为容易获得，所以并没有得到足够的重视。随着试验飞行的发展，图像采集系统的复杂化，对飞行器特征点的识别算法提出了更高的要求。

图像中特征区域识别算法经过了3个主要的发展阶段：几何特征法、颜色阈值法和理论统计法。将统计概率的方法引入图像识别领域其实是将图像检测的问题转化为模式识别的“是与否”问题。首先，利用统计分析的方法来区分特征点与非特征点样本各自的特征，其次构建相关特征的分类器，最后使用分类器完成对图像的检测。经常使用的方法有：子空间法、神经网络法、支持向量机法[1]、隐马尔可夫模型法和Boosting法。

1 AdaBoost算法

集成学习算法不同于许多单模型机器学习算法，它一般产生多个预测模型，每个模型分别对样本结果进行独立预测，单个模型预测结果之间通过加权组合等方式表决出该方法最终的预测结果。

1.1 弱学习与强学习

如果集成学习算法生成的单模型分类器之间的误差成弱相关性，那么算法的最终分类准确性要强于参与集成的单模型分类器。当单模型分类器的分类误差成相关性，则会造成参与集成的不同单模型分类器对同一样本产生同样误判的情况。集成学习算法可以分为同构集成学习和异构集成学习。由于异构算法的准确度因为学习机理不同而难以采用统一的标准来衡量，所以使用不同的学习算法会增加集成学习的复杂度，因此目前普遍研究的是同构集成学习。

集成机器学习中的弱分类器的设计是最主要的内容。与一般机器学习算法不同，集成机器学习中不需要考虑弱分类器的线性不可分问题。弱学习算法在大多数情况下比强学习算法更加容易获得。如果两者之间能够通过某种方法转换，那么生成算法的时候，仅需要找到一个略强于随机猜测的弱学习算法，便能快速将它升级为强学习算法。

1.2 AdaBoost算法

Boosting算法是图像检测领域早期最为流行的集成机器学习方法之一。最初的Boosting算法需要预知弱学习算法正确率的下限，而这在实际使用的过程中无法实现[2]。Adaboost算法对常用的Boosting算法进行了改进和提升，在算法迭代时，根据每一轮的计算数据对初始样本权重重新调整，降低正确分类的样本权重，平衡给错误分类的样本。算法在每一轮迭代中集中主要精力应对难以检测的样本，生成新的权重关系。每次迭代所产生的弱学习算法根据加权组合的方式组合成最终所需的强学习算法。AdaBoost算法生成过程如下所示[3]：

1）首先确定训练集：S＝{（x1，y1），…（xm，ym）}，其中xi∈X，为训练样本集；yi∈Y，为分类标志，并且Y∈{－1，+1}。

2）其次，初始化权值：D1（i）＝1/k，i＝1，2，…，k。

3）对于T轮循环，有t＝1，2，…，T：

a）对有权重分布的训练集学习，生成最初的预测函数hi：x→{－1，+1}；

b）计算预测函数ht的错误概率：εt＝Pr（i，Di），当εt＝0或者εt≥0.5时结束算法，且令T＝t－1；

c）令∂t＝0.5×ln[（1－εt）/εt]；

d）更新样本的权重D：

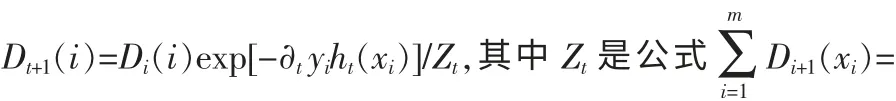
4）T轮训练结束后，获得的结果预测函数是：H（x）＝sign

公式中的∂t是经过第t轮训练后生成的弱分类器hi（x）的性能评价因子，它的值由hi（x）作用于样本集所产生的分类错误的样本权重之和εt来决定。所以，∂t是εt的减函数，当εt越小时∂t越大，说明该分类器hi（x）的重要性越高。

在训练算法的过程中，当弱分类对样本的识别误差εt≥0.5时，说明该分类器弱于随机分类，无法使用，并且算法中止。这种情况下，在样本跌代过程中，容易识别的样本权重变大，难以识别的样本权重减少，算法的更新机制失去效果。当εt＝0时，训练集的所有样本都能够被正确的区分，所有样本权重为零。

强分类器H（x）对训练样本集识别的错误率称为训练误判率，记为ε，则有：

由公式（3）可以发现，训练误判率ε与训练轮数T成指数相反关系，即T越大时ε呈指数减小。在特殊情况下，假设所有的hi（x）误判率都相等，则上式可等价为：

在集成学习算法中，强分类器的有效性与弱分类器的数量和误判率密切相关。只要有足够的资源训练出足够多的弱分类器，就可以有效的降低强分类器的误判率。就一般两分类问题而言，只需要弱学习算法的准确性略高于随机猜测，就能够使Adaboost算法最终收敛。

2 AdaBoost算法与特征点识别

2.1 Harr-like特征

图像的特征一般是指图像的纹理和形状特性，它无法直接从原始像素中获得，而是需要对具有相关性的像素进行编码和归纳。Viola等[4]在此基础上作了扩展，使用3种类型4种形式的矩形特征，分别称之为2－矩形特征、3－矩形特征、4－矩形特征，2－矩形特征又分为AB两种，如图1所示。

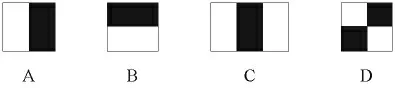
图1 Viola特征库Fig.1 Viola characteristic bank

矩形特征的数目越多，所对应的弱分类器数目也越多，AdaBoost算法挑选最优弱分类器的选择范围也就越大。增加的弱分类器中，AdaBoost算法将选择优于原弱分类器的进行添加。强分类器的性能和结构伴随更多弱分类器加入而得到有效，最终提高了算法的检测速度。

根据图像的特性，增加了的6种特征原型[5]。

图2 增加的特征原型Fig.2 Increased characteristic prototype

下文中分别使用E1和E2来区分增加3个特征原型（E、F、G）与增加6个特征原型（E、F、G、H、I、J）之后的实验过程。这两个实验过程除了特征原型数量不同外，其他条件相同：它们使用相同样本集，并且训练层数都为24层，对应设置了一样的各层强分类器的检出率（0.998）和误判率（0.6）。详细实验数据及分析如下：

表1 E1的特征比例和平均概率（%）Tab.1 Characteristic proportion and average probability of E1

在2个实验中，特征原型C、D、E相对其他特征原型表现更为突出。如果以平均概率进行评判，则扩展后的6类特征E、F、G、H、I、J显示出了良好的有效性。

表2 E2的特征比例和平均概率（%）Tab.2 Characteristic proportion and average probability of E2

2.2 特征图片样本集

特征点标志在物方空间中的旋转有3种：水平旋转（俯仰）、垂直旋转（摇摆）以及法向旋转（倾斜），如图3所示。

图3 特征点旋转模式Fig.3 Rotate mode of characteristic point

文中将特征点图像在物方空间的旋转角度分为5个类别：左侧、左半侧、正面、右半侧和右侧。对应角度范围如下：[-90°，-50°]、[-50°，-20°]、[-20°，+20°]、[+20°，+50°]、[+50°，+90°]。同时，每个类别兼顾±15°的法向旋转和±20°的水平旋转。训练中使用的样本比例如表3所示。

表3 特征点样本姿态统计Tab.3 Statistics of the sample taken from characteristic point attitude

实验结果表明，几个检测器对侧面图像和摇摆图像都具有较强的识别能力。结论如下：1）特征图像样本中旋转图像的比例越大，强分类器的训练难度也就越大，两者成正比关系；2）训练集中一定比例的旋转样本能增加检测器对旋转特征图像的检测能力。

2.3 非特征图像样本集

假设非特征图像样本集容量为N，训练一个L层的检测器，并且该检测器的每层强分类器的误判率都等于f。每一层非特征图像样本能够被算法被识别的概率为1-f，在训练时每一层需要淘汰N×（1-f）个非特征点样本。当进行第i层强分类器训练时，补充的非特征图像样本需要通过前i-1层的考核，只有被所有i-1层强分类器误判的非特征图像样本才能选用至第i层的非特征点样本集中。所以第i层训练时需要输入的候选错误样本数量为：

由公式（5）可见，算法训练的层数越多，需要准备的错误样本数量成指数增长。如果设定f=0.6，N=5 000，训练第20层强分类器需要的样本数量将达到0.33亿。如此海量的样本只能通过电脑穷举来完成。

是一种选取非特征点样本的有效方法：在训练过程中准备大量的不含有特征图像的样本集，使用前i-1层强分类器对该图片样本集进行搜索识别，将误判为特征图像的样本加入到非特征点样本集中。该种方法称为“bootstrap”法。搜索的可以采取遍历穷举的策略，在大小为W×H的图片上穷举出所有w×h大小的子图像，可得到（W-w）×（H-h）个候选样本。对于一个训练系统，至少要满足最后一层强分类器的训练，因此所需要的非特征点的数目最少为：

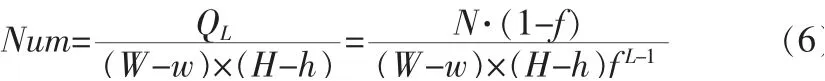
式中，N为非特征点样本集大小，f为强分类器误判率，L为级联分类器层数。

训练开始几层强分类器时有可能出现大量相似的非特征点样本的情况，本文使用如下策略进行避免：初始时以相对较大的搜索步长遍历，获得非特征点样本，用于前几层强分类器的训练；同时随着层数的增加，逐步减小搜索步长，生成更多不同的非特征点样本。

3 检测及实验结果

图4是特征图像检测系统框架，其中“检测子窗口”是指分别使用各层强分类器对子窗口进行特征图像的识别检测。通常需要进行检测识别的图像分辨率要大于样本图像分辨率（24×24），需要对图像本身进行比例的缩放，形成一个金字塔状待检图像序列。采用的插值采样的方法对待检图像进行尺度变化，按照一定的步长逐级缩小。同时，识别算法还需要对同一幅图像的不同部位进行检测。假设检测窗口每次平移k个像素，那么k的大小选择将会直接影响程序的识别精度和速度。当k的数值取得较大时，提高了检测速度，降低了检测的精度；相反，如果k值取的较小，虽然会提高检测的精度，但却大大降低了检测速度。

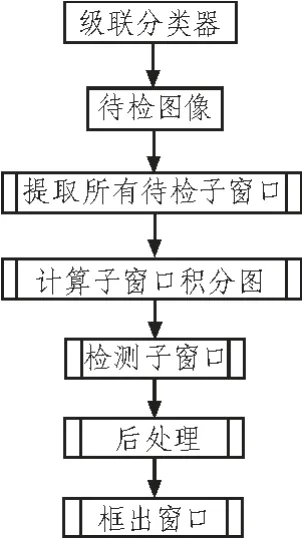
图4 检测系统框架Fig.4 Framework of detecting system

实验表明，待测图像缩放比例为1.2时，平移步长k=4，可以兼顾算法对速度和进度的双重要求，识别结果较为满意。训练和识别程序运行平台环境如下：Intel Xeon X3210四核2.13 GHz CPU、1G DDR400内存。实验结果如表4所示。

表4 实验结果Tab.4 Test results

4 结束语

飞行器特征图像识别是计算机视觉和图像处理学科在航空试飞领域的一个热点研究方向，广泛的应用于试飞实验过程中的智能安全监控、图像实时判读解析等方面。本文实验性采用AdaBoost算法，并保存分类结果以改进训练过程，提高了训练速度，综合考虑工程应用中效率与精度的需求，解决了飞行试验过程中的目标提取与跟踪问题。在此基础上，发现弱学习算法对强分类器的结构、性能有着很大影响，高效的训练算法可以加快系统的收敛速度。同时以消耗训练时间为代价，扩展矩形特征的类型数量可以有效的提高算法对特征图像的识别能力。

[1]Vapnik.The nature of statistical learning theory[M].New York：Spinger-Verlag，1995.

[2]涂承胜.Boosting理论基础[J].计算机科学，2004，31（10）：11－15.TU Cheng-sheng.The theory base of boosting[J].Computer Science，2004，31（10）：11－15.

[3]于玲.集成学习：Boosting算法综述[J].模式识别与人工智能，2004，17（1）：52－60.YU Ling.Assemble learning：a survey of boosting algrorithms[J].Pattern Recognition And Artificial Intelligence，2004，17（1）：52－60.

[4]张宏林.Visual C++数字图像模式识别技术及工程实践[M].北京：人民邮电出版社，2003.

[5]Viola P，Jones M.Robust real-time object detection.cambridge research laboratory，Technical report series[R].CRL，2001.

[6]Lienhart R，Maydt J.An extended set of Harr-like features for rapid object detection[C]//IEEE ICIP，2002：900－903.