基于多目标规划的矿车调度优化模型

冯阳阳

（西安外事学院工学院 陕西 西安 710077）

钢铁工业是国家工业的基础之一，铁矿是钢铁工业的主要原料基地。许多现代化铁矿是采用露天开采形式，其生产主要是由各种大型采矿设备间的配合来完成的。随着露天矿产量规模的不断扩大及设备大型化、机械化、自动化程度的不断提高，采运成本占矿山生产成本的比例也越来越高，优化车队运行、准确执行生产计划，以提高矿山产量，节约费用，取得较高经济效益显得尤为重要。可以说，在采运过程中运输组织方案的优劣，会直接影响到钢铁工业的经济效益。也就是说，提高这些大型采矿和运输设备的利用率是增加露天矿经济效益的首要任务。因此，如何通过合理的调度组织来提高这些露天卡车的工作效率就成为提高露天矿业经济利润的重中之重。通常来说，交通对于经济的作用主要是良好的交通状况带来了机动化程度的增长从而节约了运输时间、降低了运费、降低了产品的成本、促进了物资的流通、带动了地区间的交流等。

露天矿是在基建和生产过程中逐渐形成的。基建时期的任务是建立供电供水系统及建立运输干线，修建选矿厂、排土场及机修厂等主要构筑物和设施，以及完成投产时所必需的采准和剥离工程量。在生产过程中，为了完成计划的年矿石生产任务，必须按时完成一定的开拓、采准、剥离的工程量。露天矿在开采过程中，必须将境界内的矿、岩划分成一定厚度的水平分层，以便由上向下逐层进行开采，这些阶梯块的工作面叫做台阶。每个台阶大多使用独立的穿孔和采掘设备。由于露天开采在采出矿石的同时，必须剥离一定数量的岩石。而且，剥离岩石量的多少直接影响采出矿石的成本和单位投资额，并且随着矿山开采深度变化往往剥离岩石的数量也是变化的。而这些矿石与岩石的搬卸运输就成了露天矿场经济利益中最为重要的一环。本文将利用优化模型中整数优化的思想[1]针对这一问题展开详细讨论。

1 矿车运输组织模型的模型分析

矿车运输组织本质上属于货运车辆运行调度问题，而此问题正式货运企业运输生产管理活动中一个非常重要的组成部分。车辆运行调度工作是以车辆的运行为中心，不但是高质量完成预定的货运任务的保证，而且通过车辆运行作业计划的实施也将企业内部各生产环节（特别是车队、车间装卸部门等）连接成一个有机的整体[2]。交通运输组织是通过交通规划的手段有计划的引导交通的一系列运动，即规划者如何提示各种目标。事实上，运输组织可以理解为有限的道路空间上综合运用交通规划、交通限制和管理等手段，科学有效的地分时、分路、分车种、分流向使用道路，使交通状况始终处于有序、高效运行状态。其用意在于分解车流矛盾。一般好的交通组织主要考虑在时间上削峰填谷，避免空间上过于稀疏或者过于拥挤，体现出矛盾分散、时空均分的原则。一般对于道路通行时空资源的分配优化，重点是要解决通行能力、路权分配问题以及路网负荷均分问题。

货车运行调度工作主要内容包括：检查货运生产前的作业准备情况；检查车辆运行作业计划的执行情况；根据车辆的技术状况和所处状态，科学合理的调配车辆，提高车辆运用水平；根据主要物资的流量、流向及其变化规律，加强回程货源的组织工作，提高车辆运行水平；根据营运区域内的道路和交通情况，及时调整车辆的运行线路；合理调配劳动力，加强劳动组织工作；运用现代信息技术，对车辆和货物进行跟踪和实时控制。

对于矿车运输调度优化问题来说一般主要考虑两方面的因素。首先，它要求单位路程总运量最大；其次，要求动用的载货车量数最少。可见矿车运输调度计划编制这类问题的难点在于，如果矿车数量过少，那么矿产的运输效率将大幅度降低；相反，如果矿车数量太多，又会出现矿车现在浪费投资的现象。不难看出，矿车运输调度优化问题实际上可以看作是一个多目标优化问题[3-5]。从数学的角度来说，由于多目标规划其各个子目标之间往往是相互矛盾的（例如：我们既想矿车数量少，又想总运量最大），因此通常来说多目标问题的最大的特点就是不易获取其全局最优解。除此之外，矿产车辆的运输调度过程中往往还存在着，待优化变量规模大（即，矿产车辆的数量大、种类多）不易高效求解的问题。在现实中为了解决这类问题，人们往往采取贪心准则的优化策略，这样做的好处是，贪心准则的算法复杂度低，便于在实际中实现。但是贪心算法只能获得局部最优解而非全局最优解，这就会对实际生产中矿车运输调度的效率带来严重的影响。为了从本质上解决目前矿车运输调度存在的问题，本文提出了一种基于多目标规划思想的矿车运输调度优化模型。

在建立模型前，我们首先需要做几个模型基本的假设：1）假设卡车在铲点和卸点不存在等待排队现象；2）各个装卸点均达到规定产量；3）不考虑卡车存在偶然的交通事故。在这3条假设的基础上，我们将在下一节中介绍本文所提出的数学模型。

2 矿车运输调度优化模型的建立

在上一节中我们提到，矿车的运输组织及运行调度主要考虑2个因素，即单位路程总运量和运输作业中动用的载货车辆数。也就是说，该优化问题至少存在两个优化目标，且两个决策要求各有其合理性；同时在做最终决策时，无需强调绝对意义上的最优性，因而我们需构造一种更适用于实际决策过程的优化模型。此外，我们优化模型参与的参量主要包括矿车数量，矿产量以及单位单位路程上的矿石运输量。

下面首先针对第一个优化目标——单位路程总运量最大，建立数学模型，见式（1）。

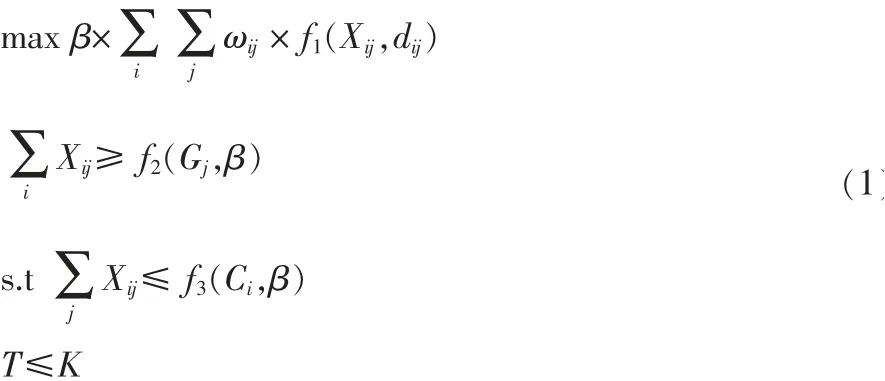
其中，f1（Xij，dij）=Xij/dij；f2（Gj，β）=Gj/β；f3（C，β）=Ci/β；β是卡车的运载量；Xij是第i个铲点到第j个卸点的运载次数；dij是第i个铲点到第j个卸点的距离；ωij是加权系数；Gj是第j个卸点的产量；Ci是第i个铲点的产量；T为动用卡车的数量；K卡车数量的上限。

这里有必要对上述模型做简要的说明。首先式（1）所给出的优化模型中，其代价函数所描述的是要求所有卡车的总的运输量最小，也就单位路程总运量最大。因为在需要运送矿石的总量不变的情况下，距离越近则意味着总运量就越小。换句话说，本优化目标的含义是要求所有载货车辆以最短的路径进行货物运输工作。此外，对于模型中约束条件简要解释，第一个约束条件是要求第个卸点的总产量必须大于或等于此卸点产量的约束；第2个约束条件是要求第个铲点运送的矿石量小于该铲点的产量；最后一个约束条件是要求卡车的数量不能超过所能采用的卡车数量极限。由此可以看出，优化模型所给出的3个约束条件能够使得本优化模型更加符合实际生产情况和相应要求。

针对目标二——动用的载货车辆数最少，建立的数学模型如下。

在模型（2）中所有的约束条件与模型（1）一致，即，是要保证在让载货车辆数最少的同时还能同时使得车辆数满足基本的货物运输要求。从数学角度上说，就是使得优化得出的车辆数不会出现“奇异值”（例如：负值），因为很显然如果没有合理的约束条件式（2）所示的优化模型的全局最优解应该为负无穷。上一节中我们提到，根据现有的运筹学技术条件，联立求解式（1）与式（2）所示的多目标优化模型并不容易，一般来说解决多目标规划一种常规思想就是将多目标转化成为单目标，这个思想下最常见的做法就是将多个目标进行线性组合，使得组合后的目标极大或者极小。本文采用一种较为新颖的基于“极大极小”的优化思想的转化策略将这个双目标问题转化成为一个单目标问题后再进行求解[6]，转化后模型如下所示。点法，梯度下降法和空间投影法等一些优化领域里的成熟的算法进行求解[7]。值得一提的是，由于式（3）所示的模型其求解简单，所以式（3）所示的优化模型还可以根据实际需要在约束条件中继续增加更多实际中所需要的约束条件，例如：运输时间，运输费用的限制等等。因此，我们说本文模型另一个优势是具有良好的推广性。

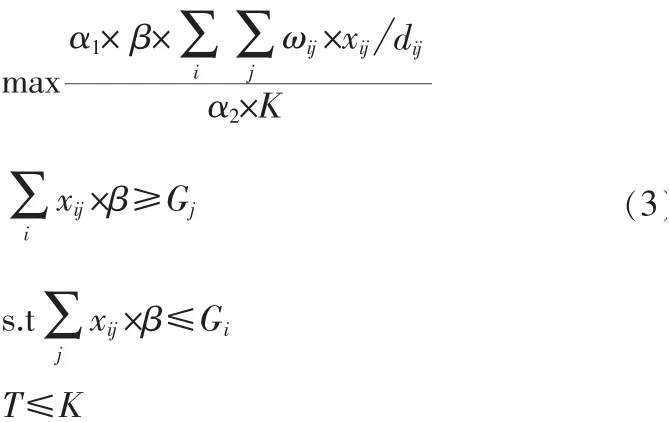
3 模型结果分析

从式（3）不难看出，此时通过合理转化，我们已经将原有的多目标优化问题简化成为了一个单目标优化问题，使得式（3）最小的条件此时显然是使得式（1）与式（2）一起最小的必要条件。虽然，式（3）所示的优化模型是一个非线性规划模型，但是由于分子和分母都是线性函数，因此可以方便的使用内

为了验证上一节给出的矿车运输调度优化模型的可行性，在本节中我们将采用某矿场的实际数据进行算法模拟。这里将分别采用本文提出的方法和传统的贪心算法进行比较，采用对比分析法验证本算法的优越性。

某矿场的实际生产数据如表1所示。

表1 矿场数据分布Tab.1 Mine data distribution

通过将表1所示的矿场分布数据带入上一节给出的矿车运输调度优化模型，计算得出的单位运量24.89万吨，而同时执行该计划所需矿车仅为25量。相应的，传统贪心算法得到的单位运量仅为21.543万吨，所需矿车为29量。从实验结果对比很容易看出，本文提出的基于多目标优化的方法相较于传统的优化方法有明显的优势。

4 结 论

交通组织是指通过交通规划的手段有计划的引导交通的一系列运动，使得机动化程度的增长从而节约了运输时间、降低了运费、降低了产品的成本、促进了物资的流通。矿车交通组织的合理优化是提高矿区生产效率的核心问题，是能够提高矿区经济效益的有效途径。本文利用运筹学中多目标优化的思想提出了一种矿车运输调度优化模型，并且通过极大极小的方法将双目标问题转化为一个单目标问题，简化了求解过程。通过对比分析可以看出，本文所设计的算法远远优于传统的贪心算法，因此适于应用到实际的矿车生产调度工作中，体现其重要的实践指导意义。

[1]《运筹学》教材编写组.运筹学[M].北京：清华大学出版社，2005.

[2]戴彤焱，孙学琴.运输组织学[M].北京：机械工业出版社，2011.

[3]吴祈宗.运筹学与最优化方法[M].北京：机械工业出版社，2008.

[4]胡斌，王国平，李国强.采用多目标改进差分进化算法的环境经济发电调度[J].陕西电力，2013（1）：24－27.HU Bin，WANG Guo-ping，LI Guo-qiang.Probe into environmental economic dispatching adopting multiobjective improved differential evolution algorithm[J].Shaanxi Electric Power，2013（1）：24－27.

[5]宁姗.基于蚁群聚类的多目标环形分类的方法研究[J].工业仪表与自动化装置，2012（5）：70－73.NING Shan.Research on annular sort of multi-objects based on ant colony clustering[J].Industrial Instrumentation&Automation，2012（5）：70－73.

[6]姜启源，谢金星，叶俊.数学模型[M].北京：高等教育出版社，2010.

[7]陈宝林.最优化理论与方法[M].北京：清华大学出版社，2005.

[8]Giordano，F.R.等著.叶其孝等译.数学建模[M].3版.北京：机械工业出版社，2005.