基于小波与LS-SVM集成的模拟电路故障检测

彭四海

（中国空空导弹研究院 河南 洛阳 471009）

模拟电路故障诊断是电路理论热点问题。由于电路的元件参数容差大，且存在反馈回路，模拟电路故障呈现多样性、离散性和非线性等特点。近年来，随着智能信息处理技术发展，研究者们相继提出了基于神经网络[1]、小波分析[2]、支持向量机[3-4]和基于模糊理论[5]等模拟电路故障诊断方法，并取得了比较好的识别效果。

文献[6]表明，电子电路诊断测试中80%的故障来自于模拟阶段。现有的模拟电路诊断测试方法很大程度上依赖于模拟数据，而模拟数据的准确性受到元件容差、故障机理的复杂性、非线性问题和由于操作和环境引起的元件参数的偏差等影响。因此，当元件在其容差范围内变换时，检测并隔离故障是一个具有挑战的问题。 近年来，各种模拟电路故障诊断技术被提出[3-4，7]。这些技术主要基于所选电路的某些节点的偏微分诊断方程或在模拟的数据集上进行。这些方法局限于评估过程的非线性且不能访问电路的内部节点的状态。

支持向量机（Support Vector Machines，SVM）是一种通过结构风险最小化来在学习能力与泛化能力之间取得折中的机器学习方法，尤其适用于小样本的分类学习问题。小波分析是一种时频分析方法，适合分析非平稳信号，小波分析在多分辨分析基础上构造的一种更精细的分析方法，更能反映出数据的主要特征。近年来，这两种方法都被成功地应用于故障预测，但应用于模拟电路的研究较少。基于SVM的模拟电路故障预测主要集中于分类器的集成研究上[3-4]，但这些方法易出现数据不平衡和正则化因子的选择问题。针对已有方法的不足，文中利用小波分析解决模拟电路特征提取的不平衡问题，然后利用最小均方支持向量机（Least Squares SVM，LS-SVM）解决少样本的优势，对模拟电路中的故障进行分类，建立相应的分类模型。

1 故障预测框架

图1 模拟电路故障检测检测框架意图Fig.1 Illustration of analog circuit fault diagnosis framework

该故障检测框架主要由扫描信号生成器、频谱估计估计器、特征提取单元与机遇LS-SVM的多分类器构成。对大部分电子电路来说，其行为特征都表现为对一些频率脉冲的响应。所以本文使用频率特征的响应作为故障检测的信号。为了获得频域特征，电路测试单元需要被扫描信号生成器的信号激活（扫描信号生成器的频率宽度比电路测试单位的要大）。然后对电路测试单元的脉冲响应功率谱密度进行估计并提取电路测试单元的频域特征信息。此处，文中使用的是基于Welch方法的非参数估计方法来估计功率谱密度。文中抽取了两类特征：1）常规的频率特征；2）基于小波变换后的频率特征作为故障检测的输入。

模拟电路故障检测的过程包含两个阶段：训练阶段和诊断阶段。实际应用中通常以最常发生的故障作为需要检测的故障。电路测试单元模拟这些需要检测的故障。故障被存储在一个字典中以便进行在线的故障预测时使用。在检测阶段，电路测试单元被输入的脉冲信号激活并获得相应的特性信息，这些特征信息与故障字典中的信息进行比较，以确认故障的种类。

2 特征选择与提取

文中利用小波变换将两种特征从电路测试单元响应的交换的信号功率谱密度中提取出来。一般地，处理模拟信号有4种类型的滤波器：低通滤波器、高通滤波器、带通滤波器和带阻滤波器。

2.1 常规频率特征

常规频率特征指可以在频域内标识电路行为的元件的特征。对于带通滤波器，可操作的特征定义为：1）中心频率（f0）；2）3 dB的带通上下界限值（fl和fu）；3）频率响应的最大值（H（f0））。类似，对于低通滤波器，中心频率和最大频率响应H（f0））也是特征向量的一部分。除此之外，在低通滤波器中，3 dB的截止频率（fcut）也用来作为特征向量的一部分。其他的特征也可以增加分类的准确性。因此，带通滤波器和低通滤波器的常规频率特征表示如下：

高通滤波器和阻通滤波器的常规特征选取也类似，只是截止频率和带通上下界限值不一样。

2.2 小波变换特征

为了提高故障分类的准确性，通过小波变换将额外的特性信息添加到了特征向量中。此处，频率响应P（f）通过多尺度小波变换被分解为近似与细节信号：

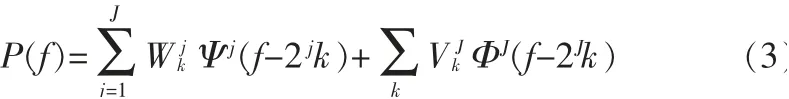
其中，Ψj（f）是小波函数，ΦJ（f）是尺度函数。近似细节信号通过近似于小波系数表示，这些系数可以通过低通和高通滤波器得到。文中使用Haar小波，信号的变换层次为1到5层。因此，不同层次上的小波信号分解的能量用来作为特征向量的一部分，表示为如下：

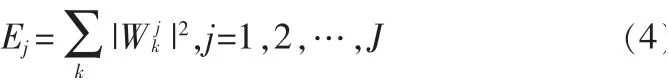
其中，Wj

“咦？”霍铁和小达忍不住叫了出来。小达仔细端详着小姑娘，然后哈哈大笑起来。她扭头扯了扯霍铁的胳膊：“哥哥，你忘了？几个月前的那次体操表演赛，我还采访过她呢！”

k是在第j个层次的小波分解的第k个小波系数，J为预先设定的分解层次。能量指示器容易实现，但没有利用到小波变换的所有信息。在下面的一个小波变换特征中，文中使用均值（μj）和标准方差（σj）作为小波分解每一个层次的特征：

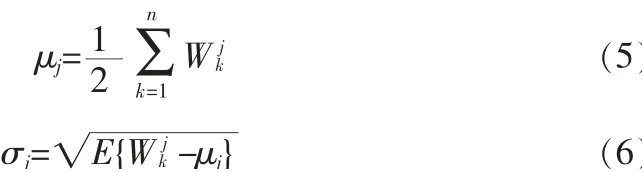
此处n表示预先设定的作为特征的系数的数目。

因此，带通滤波器最终的包含通过小波变换的特征向量形式如下：

或文中对不同的条件进行了测试，这些条件主要基于：1）频率特征类型；2）小波特征类型；3）规范化方法。其中，频率特征类型是指特征向量中的分量包含滤波电路的常规频率特征、小波特征或常规频率特征和小波特征的组合。当选择小波特征时，能量指示器、能量均值或能量标准方差用来表示特征向量。规范化方法用来进一步增强这些特征，使用规范化方法可以避免不同属性纬度较大取值偏差带来的分类准确性影响。表1为文中使用到的测试条件参数。

表1 测试参数Tab.1 Test parameter table

3.1 LS-SVM分类器

与传统的分类方法相比，支持向量机具有很好的推广（泛化）能力。SVM利用一个核函数（kernel）将输入数据映射到一个高维度的可以线性划分的特征空间。这个过程可以抽象为一个比较复杂的二次规划问题。LS-SVM可以减少这个二次规划问题的复杂度和计算量。

给 定 一 个 向 量 数 据 集 合{（x1，y1），…，（xn，yn）}，其 中xi∈RN，yi∈{+1，-1}，i=1，…，n。支持向量机的目的是构建一个具有形式wTf（xi）+b分类器，该分类器满足约束条件yi（wTf（xi）+b）≥1，其中f（xi）是一个将输入映射到高维度空间的非线性函数，w是一个M维的垂直于分类超平面的权值向量，b是一个阈值。为了容忍一定的错误分类，二次优化模型中引入了一个松弛变量ξi。支持向量机的分类器设计如下：

其中，0≤αi≤C，i=1，…，n。

3.2 多类别SVM分类器

多个故障分类问题一般通过结合多个两类LS-SVMs分类器来完成。一对一LS-SVM在多个类别的样本间提供了最好的分类性能。对C个类别的分类问题，一对一LS-SVM需要构建C（C-1）/2个分类器，这些分类器都需要按照两类分类器的算法进行训练。当训练完毕后，需要通过投票来进行进一步的测试。当所有的分类器都构建好后，需用下面的决策函数来进行投票：

其中，wij和bij分别为第i和j类的权值和阈值。最后通过下面的规则来对数据集进行判类：

其中，Γi（x）=∑Csgn（Γij（x））。如果公式（11）满足某个类i=1，j≠i别i，则x被划分为第i类，如果公式（11）对多个类别i都满足，则x是不可分的。

4 实验分析

文中故障检测实验分析使用的电路是模拟滤波电路。该电路是一个如图2所示25 kHz Sallen-Key带通滤波器，元件容差范围为10%。电路的频率响应在元件C1，C2，R2和R3的容差范围内变化时，电路的状态属于无故障状态（记为NF）。但当这4个元件中的任一一个超出其容差范围，但其他元件没有超出其容差范围时，则产生一个由表2里面描述类别的故障响应。这些故障响应和NF类别的响应一起构成一对一多类LS-SVM分类器的输入。

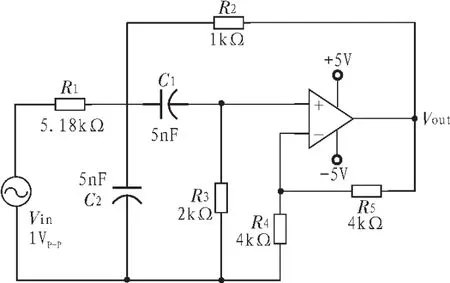
图2 实验使用的25 kHz的Sallen-Key带通滤波器Fig.2 Illustration of 25 kHz Sallen-Key band filter

如表2所示，实验中只考虑元件值超过最大/小值的10%或最大值超过标准值200%的取值。实验的设置如图3所示。在图3中，当获得响应信号后，通过Welch[8]方法对该信号的能量谱进行估计，然后从能量谱中抽取一些特征信息作为LS-SVM分类器的输入。本文使用的是1-1多类别的LSSVM分类器，选取RBF作为核函数，支持向量机集成中各参数初始值选取为：σ=1，C=5，μσ=3.5，μC=4，训练和优化了36个类别的二类分类器，其中训练的数据集为30个人为设置了故障信息的信号。SVM分类器在表1中列出的所有测试条件上都进行了验证。表3为LS-SVM分类器的测试精度和测试时间。

表2 Sallen-Key滤波器的故障类型Tab.2 Fault categories of Sallen-Key filter

图3 故障预测实验设置Fig.3 Fault diagnosis test settings

文中，测试准确度定义为测试样本中被正确分类样本的比例，测试时间定义为测试所有样本消耗的时间。从表3可以看出，在所有的测试条件中（C1~C13），测试条件C13在测试准确度和测试时间上都超过了其他测试条件。其原因是C13通过小波变换后的特征更有利于分类的判别。从表3还可以看出，当只考虑常规频率特征（C1）或小波特征（C4，C6）时，小波特征的分类精度和分类时间都比常规特征的少。但需要注意的是，当只考虑小波特征且使用了规范化后（C7），测试的精度会下降。

表3 实验结果Tab.3 Experimental results

进一步的对比（C4，C5）和（C6，C7）可以看到，从小波系数里面提取的统计特征的分类性能比基于能量谱的分类性能更好。

为对比和已有算法的性能，本文在带通滤波器上与主流的故障检测算法，如单一支持向量机（o-v-o SVM）、径向基神经网络（RBFNN）、BP神经网络（BFNN）和APSVM[14]进行了故障诊断仿真对比测试，测试结果如表4和表5所示。

表4 在Sallen-Key带通滤波器上的故障预测方法比较Tab.4 Fault diagnosis methods comparison over Sallen-Key band filter

测试结果表明文中的方法在带通滤波器电路上进行故障诊断的训练错误率和测试错误率比单一SVM和两种神经网络方法低很多，比APSVM的性能也要好，因此文中的方法具有较低的错误率和很好的推广能力。

5 结 论

文中提出基于最小二乘支持向量机的模拟电路故障预测方法。通过小波变换，提取了更为有利于故障分类的特征信息，在各种测试条件下测试了提出的故障分类方法。实验分析表明，基于小波变换和LS－SVM的故障预测方法与同类方法相比具有很高的精确度，同时也具有很好的推广能力，对模拟电路故障预测效果明显。

[1]Aminian F，Aminian M.Analog fault diagnosis of actual circuits using neural networks[J].IEEE Transaction on Instrumentation and Measurement，2002，51（3）：544－550.

[2]Long Bing，Huang Jianguo，Tian Shulin.Least squares support vector machine based analog circuit fault diagnosis using wavelet transform as preprocessor[C]//Proceedings of the International Conference on Communications，Circuits and systems，2008：1026－1029.

[3]马超，陈西宏，徐宇亮.基于支持向量机属性约简集成的模拟电路故障诊断[J].仪器仪表学报，2011，32（3）：660－666.MA Chao，CHEN Xi-hong，XU Yu-liang，et al.Analog circuit fault diagnosis based on attribute reduct ensemble of support vector machine[J].Chinese Journal of Scientific Instrument，2011，32（3）：660－666.

[4]唐静远.模拟电路故障诊断的特征提取及支持向量机集成方法研究[D].西安：电子科技大学，2010.

[5]Bilski P，Wojciechowski J.Rough-Sets-Based reduction for analog systems diagnostics[J]. IEEE Transaction on Instrumentation and Measurement，2011，60（3）：880－890.

[6]HESS A，FILA L.The joint strike fighter（JSF）PHM Concept：Potential impact on aging aircraft problems[C]//Proceedings of IEEE Aerospace Conference，Big Sky，Montana，USA，2002，6：3021－3026.

[7]Feng L，Woo P.Fault Detection for Linear Analog IC：The Method of Short-circuit Admittance Parameters[J].IEEE Transaction.on CAS－1，2002，49（1）：105－108.

[8]Welch P.The use of fast fourier transform for the estimation of power spectra：a method based on time averaging over short，modified periodograms[J].IEEE Transactions on Audio Electroacoust.，1967，15（2）：70－73.