耦合结构对音叉式陀螺振动特性的影响*

孙香政，王 刚，郭志想，陆志东

(中航工业西安飞行自动控制研究所，西安710065)

微机电系统MEMS(Micro-Electro Mechanical Systems)是20世纪80年代随着硅微机械加工技术的发展而逐渐成长起来的。MEMS的特征尺度在微米量级，集传感技术、致动技术和控制技术于一体。随着MEMS技术的发展，MEMS陀螺越来越多地应用于惯性导航技术中。与其他惯性导航器件相比，MEMS陀螺具有重量轻、体积小、成本低和便于大批量生产的优点，在军用和民用领域都有着广阔的发展前景。

传统MEMS振动陀螺采用单质量块敏感科氏力，从而反应角速率信号。外界振动与加速度信号会直接影响单质量块陀螺的输出，严重影响陀螺性能［1－2］。针对单质量块陀螺的缺点，目前广泛采用的方案是使用差分式结构的音叉式陀螺，通过差分输出信号降低振动与加速度信号的干扰［3－5］。音叉式陀螺结构设计的要点是获得同频、等幅、反向的振动模态［6－8］。受工艺与电路的限制，两个独立的单质量块陀螺难以实现上述要求，需要引入耦合结构。常见的耦合结构为弹性梁和杠杆，以及其衍生结构。使用弹性梁作为音叉式陀螺的耦合结构，具有结构简单、工艺实现难度低、线性度好等优点，但存在同向振动模态频率低于反向振动模态频率的问题。使用杠杆作为音叉式陀螺的耦合结构，能够使同向振动模态频率高于反向振动模态频率，提高振动性能，但其结构复杂、工艺控制难度大，线性度差。因此，目前大多数陀螺的耦合结构都采用弹性梁结构。

本文针对使用弹性梁作为耦合结构的音叉式陀螺结构，阐释其工作原理，建立振动模型。通过理论计算与有限元仿真，分析音叉式陀螺振动特性，并提出弹性梁耦合结构的设计准则。

1 工作原理

如图1所示，一种典型的音叉式陀螺包括对称的两个单质量块陀螺结构，以及中间的耦合结构。陀螺工作时，驱动电极施加电信号，通过电容变化产生驱动力，分别驱动左右两部分沿x轴同频、等幅、反向振动。当有z轴角速率信号输入时，产生科氏加速度，敏感质量块沿y轴同频、等幅、反向振动。通过对检测电容进行差分运算，可以解算角速率信号。

图1 音叉式陀螺结构示意图

对于单质量块陀螺，当任意轴向上有线加速度信号时，检测电容都会发生变化，即产生角速率信号输出值。而对于音叉式陀螺，线加速度信号引起两侧质量块产生同向位移，检测电容变化趋势一致，通过差分计算，输出角速率值不变。

实际情况中，由于工艺与电路的限制，左右两部分的质量、刚度系数、阻尼、驱动力幅值等不完全对称［9－10］。在驱动力激励下做简谐振动时，左右两部分可能出现振动特性不对称，引起差分结果的偏差。另外，如果左右两部分独立振动，二者谐振频率的差别和驱动力相位不对称会增加电路后处理的难度［5］。

2 理论计算

2.1 物理模型

如图2所示，将陀螺驱动模态简化为一个二自由度系统［11－13］，耦合结构为弹性梁，简化为一个刚度为k0的弹簧，研究其受简谐力作用的情况。根据音叉式陀螺的工作原理，施加在左右两侧的驱动力相位相差180°，沿x轴方向作用。

图2 音叉式陀螺驱动模态物理模型

设定坐标系如图2，系统动力学方程为

其中，x1和x2分别为驱动模态下两侧的位移，F1和F2分别为两侧驱动力的幅值，m1和m2分别为两侧敏感质量，D1和D2分别为两侧的阻尼，k1和k2分别为两侧的总刚度，k0为耦合弹簧的刚度。

设

其中，C1和C2分别为两侧驱动位移的幅值，代入式(1)，得

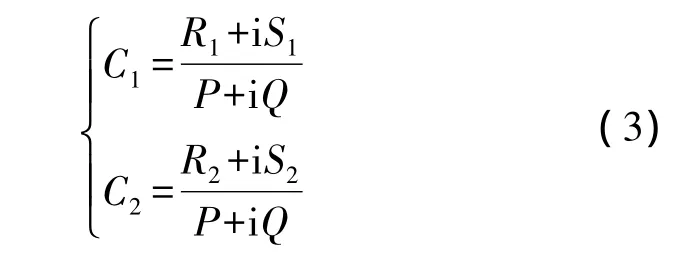
其中

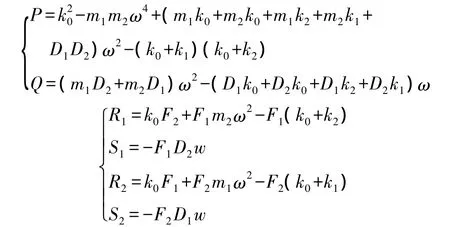
使用|C1|/|C2|表示振幅的不对称性。根据式(3)，得振幅不对称性为

系统自由振动时，式(1)变为

将式(2)代入，可得

求解ω，即系统的固有频率为k0的函数。

2.2 振幅不对称性与弹簧刚度关系

由于工艺和电路引起的陀螺不对称性可以简化为刚度不对称、驱动力幅值不对称和质量不对称3种情况，下面分别研究系统在3种情况下的运动特性。

2.2.1 刚度不对称

k1≠k2，m1=m2=m，D1=D2=D，F1=F2=F 时，式(4)变为

振幅不对称性由驱动力频率、陀螺两侧的频率、质量和阻尼决定。当驱动力频率ω为常数时，振幅不对称性与耦合弹簧刚度k0无关。实际陀螺工作时，应该将驱动力频率ω设置为与系统固有频率ωn相等，此时振幅不对称性为耦合弹簧刚度k0的函数，改变k0对振幅不对称性有影响。

2.2.2 驱动力幅值不对称

F1≠F2，k1=k2=k，m1=m2=m，D1=D2=D 时，

对于系统自由振动的情况，由式(6)可得

对于系统受迫振动的情况，根据式(3)与式(9)，

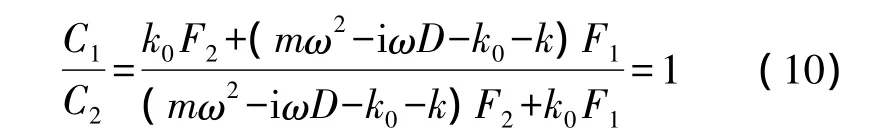
因此，系统在任意谐振频率下的振型都与主振型相同。在该情况下|C1|/|C2|≡1，与耦合弹簧刚度k0无关。

2.2.3 质量不对称

m1≠m2，k1=k2=k，D1=D2=D，F1=F2=F 时，式(4)变为

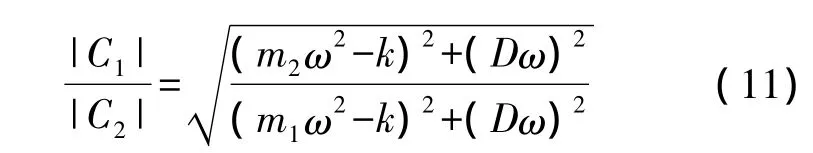
与刚度不对称的结果类似，振幅不对称性由驱动力频率、陀螺两侧的频率、质量和阻尼决定。当驱动力频率ω为常数时，振幅不对称性与耦合弹簧刚度k0无关。驱动力频率ω设置为与系统固有频率ωn相等时，振幅不对称性为耦合弹簧刚度k0的函数，改变k0对振幅不对称性有影响。

3 有限元仿真

3.1 有限元模型

MEMS陀螺设计过程中，可以通过有限元软件进行仿真分析，提高设计效率。动力学分析的目的是确定惯性和阻尼等起作用时结构的动力学行为。利用ANSYS软件对音叉式陀螺进行动力学分析，包括模态分析和谐响应分析两部分。模态分析能够获得结构的固有频率，谐响应分析能够获得结构在已知频率和幅值在正弦载荷作用下的稳态响应。

根据典型的陀螺结构，建立如图3所示的质量等效简化模型。

图3 音叉式陀螺结构简化模型

仿真参数采用单晶硅材料参数，其中密度ρ=2 329 kg/m3，弹性模量 E=130 GPa，泊松比 μ=0.28，阻尼比 ξ=1×10－5。

通过改变耦合梁的几何尺寸，调整其刚度。分别在刚度不对称、驱动力幅值不对称和质量不对称3种情况下进行动力学分析，驱动力频率分别设定为系统固有频率和非固有频率，研究耦合梁刚度变化对陀螺振动特性的影响。

3.2 仿真结果

3.2.1 刚度不对称

通过改变左右两侧弹性梁的几何尺寸，调整其刚度，使k1=0.9k2。驱动力频率与系统固有频率相同的情况下，|C1|/|C2|与耦合梁长度的关系如表1所示。

表1 刚度不对称、固有频率下耦合梁与振幅不对称性关系

仿真值与计算值一致。k0对系统固有频率有影响，进而影响工作在固有频率点的陀螺振幅不对称性。k0越大，振幅不对称性越小。

在非固有频率下激励，取驱动力频率为f=10 000 Hz，|C1|/|C2|与耦合梁长度的关系如表2所示。

表2 刚度不对称、非固有频率下耦合梁与振幅不对称性关系

仿真值与计算值一致。当驱动力频率为恒定时，k0对陀螺振幅不对称性无影响。

3.2.2 驱动力幅值不对称

设置驱动力幅值F1=0.9F2。驱动力频率与系统固有频率相同的情况下，|C1|/|C2|与耦合梁长度的关系如表3所示。

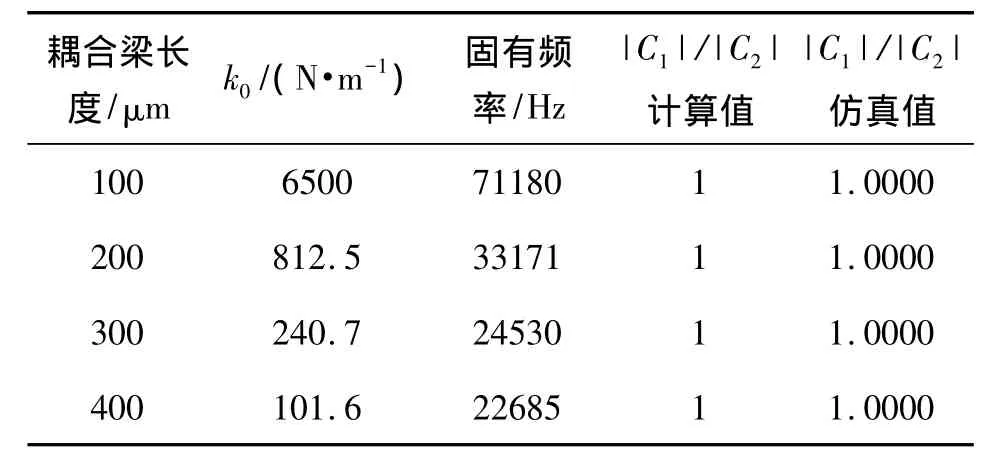
表3 驱动力不对称、固有频率下耦合梁与振幅不对称性关系

在非固有频率下激励，取驱动力频率为 f=10 000 Hz，|C1|/|C2|与耦合梁长度的关系如表4所示。

表4 驱动力不对称、非固有频率下耦合梁与振幅不对称性关系

仿真值与计算值一致。驱动力幅值不对称对陀螺振幅不对称性无影响。在该情况下，振幅不对称性恒为1。

3.2.3 质量不对称

通过改变左右两侧质量块的几何尺寸，调整其质量，使m1=0.9m2。驱动力频率与系统固有频率相同的情况下，|C1|/|C2|与耦合梁长度的关系如表5所示。

表5 质量不对称、固有频率下耦合梁与振幅不对称性关系

仿真值与计算值一致。k0对系统固有频率有影响，进而影响工作在固有频率点的陀螺振幅不对称性。k0越大，振幅不对称性越小。

在非固有频率下激励，取驱动力频率为 f=10 000 Hz，|C1|/|C2|与耦合梁长度的关系如表6所示。

表6 质量不对称、非固有频率下耦合梁与振幅不对称性关系

仿真值与计算值一致。当驱动力频率为恒定时，k0对陀螺振幅不对称性无影响。

4 结论

对于音叉式陀螺，当驱动力频率恒定时，在刚度不对称、驱动力幅值不对称和质量不对称3种情况下，耦合结构的刚度对陀螺振幅不对称性无影响。但是，耦合结构的刚度对音叉式陀螺的固有频率有影响，进而影响工作在固有频率点时陀螺的振型。通过提高耦合结构刚度，提高陀螺固有频率，能够有效降低振幅不对称性。设计陀螺时，需综合考虑对固有频率和对振幅不对称性的需求，调整左右两部分的刚度和质量以及耦合结构的刚度。

［1］ Singh T P，Sugano K，Tsuchiya T，et al.Analysis of Acceleration Sensitivity in Frequency Decoupled MEMS Tuning Fork Gyroscope［J］.Procedia Engineering，2011，25:51－54.

［2］ 陈伟平，郭玉刚，陈晓亮，等.双质量块微振动陀螺设计与仿真［J］.哈尔滨工业大学学报，2009，41(7):30－33.

［3］ Trusov A A，Schofield A R，Shkel A M.Vacuum Packaged Silicon MEMS Gyroscope with Q-Factor Above 0.5 Million［J］.IMAPS Device Packaging Conference 2010，March 2010:152－153.

［4］ Tatar E.Quadrature Error Compensation and Its Effects on the Performance of Fully Decoupled MEMS Gyroscopes［D］.M.S.Thesis，Middle East Technical University，September 2010.

［5］ Green J A，Sherman S J，Chang J F，et al.Single-Chip Surface Micromachined Integrated Gyroscope with 50°/h Allan Deviation［J］.IEEE J of Solid-State Circuits，2002，37(12):1860－1866.

［6］ Sharma，Zaman M F，Zucher M，et al.A 0.1 °/h Bias Drift Electronically Matched Tuning Fork Mircogyroscope［J］.IEEE MEMS 2008，Jan.2008:6－9.

［7］ Zaman M F，Sharma A，Ayazi F.High Performance Matched-Mode Tuning Fork Gyroscope［J］.Proc IEEE MEMS 2006，2006:66－69.

［8］ Sharma，Zaman M F，Amini B，et al.A High-Q In-Plane SOI Tuning Fork Device［J］.IEEE Sensors 2004，Oct.2004:467－470.

［9］ Trusov A A，Schofield A R，Shkel v.Micromachined Rate Gyroscope Architecture with Ultra-High Quality Factor and Improved Mode Ordering［J］.Sensors and Actuators A，2011，165:26－34.

［10］ Azgin K，Temiz Y，Akin T.An SOI-MEMS Tuning Fork Gyroscope with Linearly Coupled Drive Mechanism［J］.MEMS 2007，Jan 2007:607－610.

［11］ Thomson W T，Dahleh M D.Theory of Vibration with Applications［M］.Beijing:Tsinghua University Press，2005:49－147.

［12］迟晓珠，崔健，闫桂珍.MEMS陀螺振动特性试验技术［J］.传感技术学报，2008，21(4):559－562.

［13］刘恒，何晓平，苏伟，等.微机械音叉写真器动力学分析与仿真［J］.传感技术学报，2009，22(3):325－330.