面向无线传感结构健康监测的压缩感知方法研究*

季 赛 ，黄丽萍，孙亚杰

(1.南京信息工程大学/江苏省网络监控工程中心，南京210044;2.南京信息工程大学信息与控制学院，南京210044;3.南京航空航天大学/机械结构力学及控制国家重点实验室，南京210016)

随着无线传感器网络WSNs(Wireless Sensor Networks)在结构健康监测SHM(Structural Health Monitoring)领域的应用越来越深入，近些年来面向结构监测的无线传感器网络(WSN_SHM)的数据压缩技术吸引了越来越多的学者的关注。结构监测领域，需要布置大量的传感器节点，通过较高频率的采样率进行数据采集和实时监测，为了平衡网络的能量、降低数据存储和传输的带价，需要对原始数据进行压缩。2006年，Zhang和Li提出基于提升小波变化的数据压缩算法［1］，该方法是一种有损的数据压缩算法，可以实现很高的压缩效率。同年，Zhang和Li提出基于有外界输入的线性自回归模型的地震响应数据压缩方法［2］。2006年，美国南加州大学的Chintalapudi K K提出了线性预测编码［3］LPC(Linear Predictive Coding)的数据压缩方式，该方法是无损数据压缩，采用基于自回归移动平均(ARMA)模型的预测算法对结构健康监测的采集数据进行无损压缩。2007年，美国Lehigh大学土木与环境工程系的Zhang Y F在其结构健康监测应用中，采用线性回归法［4］消除节点所采集数据的时间相关性，实现了数据的压缩传输。

以上方法都属于传统的数据压缩算法，即先采集到完整的原始数据，然后在传感器节点对数据进行压缩处理。最近几年，一种新的数据压缩算法压缩感知CS(Compressive Sensor)被提出来用于直接采集压缩格式的数据。该方法最初是用于图像处理等方面，随着该理论的不断深入研究，目前该理论被应用于无线传感器网络［5－6］、声学［7－8］、水下监测［9］、遥感［10］等领域。而在结构健康监测领域，国外学者Morlier和Bettebghor［11］将压缩采样技术应用到了结构模态振型的重构中去，并对平板结构进行了分析，可以通过少量测点即可重构结构的振型。Cortial［12］等人提出了DDDAS(Dynamic Data Driven Applications System)方法将压缩感知应用到结构健康监测领域。此外，文献［13－14］都从不同的技术方法上验证了压缩感知理论在结构监测领域的可行性。国内对将压缩感知理论应用于结构健康监测领域的研究刚起步，哈尔滨工业大学鲍跃全等人［15］利用基于压缩感知的理论优势，研究了结构健康监测振动响应数据的Bayesian压缩感知方法。

目前，由于压缩感知理论巨大的应用价值，基于压缩感知的结构监测的数据压缩技术已经展现出美好的应用前景。本文将分析感知压缩的原理、提出基于压缩感知的结构健康监测方法CS_WSN_SHM(Compressed Sensing Structural Health Monitoring Based on Wireless Sensor Network)，给出了结构健康监测信号的稀疏化表示，研究了改进的信号重构算法，提出了CS_WSN_SHM的处理流程。通过实验分析，对比WSN_SHM方法，CS_WSN_SHM具有较高的数据压缩比，并保持良好的损伤检测精度，减少了网络传输的能耗。

1 压缩感知理论在CS_WSN_SHM上的表述

压缩感知的核心思想是将压缩与采样合并进行，首先采集信号的非自适应线性投影(测量值)，然后根据相应重构算法由测量值重构原始信号。其特点在于信号的投影测量数据量远远小于传统采样方法所获的数据量，突破了Naquist采样定理的瓶颈，且压缩采样与采样频率无关只和信号稀疏性有关，这使得高分辨率信号的采集成为可能。

压缩感知理论主要包括3个部分:一是信号的稀疏表示;二是测量矩阵的设计，要在降低维数的同时保证原始信号的信息损失最小;三是设计信号重构算法，在测量矩阵满足约束等距性条件下，利用观测值无失真的重构出原始信号。论文将在以上3个方面分析压缩感知理论在结构健康监测中的应用。

1.1 结构健康监测中采集信号的稀疏化

信号的稀疏性(Sparsity)广泛应用于数据压缩、通信以及图像处理领域。结构健康监测领域中，多传感器节点在10 Hz到几百Hz的采样频率下，通过10次～20次的平均采样，采集长度为几百序列点～几千序列点的信号。这些信号通常不是绝对稀疏的，但如在某些变换域(例如傅立叶域、小波域、曲波域等)下近似稀疏，即认为是可压缩信号。下面给出SHM的采样信号稀疏性的定义(以航空铝板振动信号为例)。

定义1 设N维SHM采样信号x(n)∈RN，存在K个非零元素，即‖x‖0≤K，则称该信号是K稀疏的;或信号x(n)本身并不稀疏，但存在一个正交稀疏域Ψ可实现x=Ψα且‖α‖0≤K，则可称信号x(n)是近似稀疏，或在变换域Ψ上是K稀疏的。

其中α为稀疏系数，Ψ可以选择傅里叶变换的正变换矩阵，小波变换的各个小波基等。由于小波变换的各个小波基具有较高的稀疏性，本文实验中采用其中的Haar小波基来实现信号的稀疏化。

Haar小波的定义为式(1);式(2)构成L2(R)的一个正交基;通过规范化处理，式(3)构成L2(R)的一个规范正交基。

图1是在Haar规范正交基下对原始采样信号实现的稀疏化的结果。图中可以看出Haar小波基不仅可实现无噪声采样信号的稀疏化，如图1(c)的稀疏度K=44;对含有噪声的结构健康监测的采样信号也同样具有良好的效果(稀疏度K=46)。

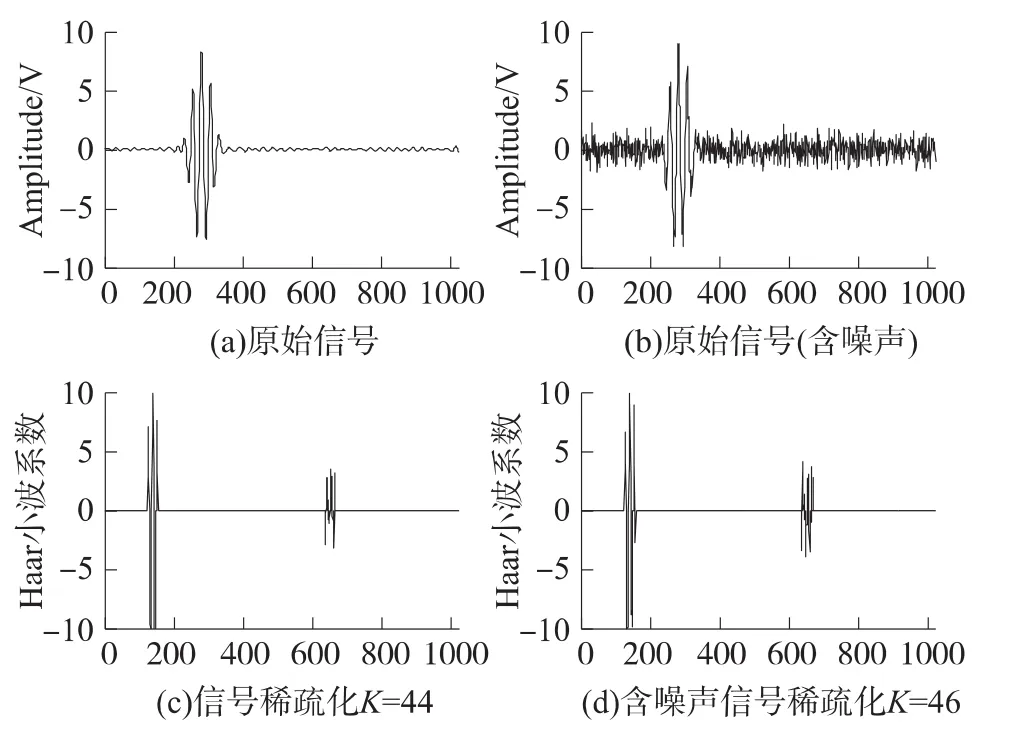
图1 SHM中采样信号的稀疏化

1.2 CS_WSN_SHM的测量矩阵

在无线传感的结构健康监测中采用压缩感知的本质是对变换域Ψ上是K稀疏的信号，用一个与变换基(N×N维)不相关的测量矩阵(M×N，M≪N)将原始高维序列(N×1)投影到一个低维空间(M维)上，获得M×1维的投影测量值，从而实现信号压缩;最后再从M×1维的投影测量向量重构原始信号并用于结构健康监测。下面给出SHM中压缩感知的测量矩阵和线性投影的定义:

定义2 设N维SHM采样信号x(n)∈RN，在正交稀疏域Ψ上是K稀疏的，即x=Ψα且‖α‖0≤K。设某一个测量矩阵Φ∈RM×N(M≪N)，信号x在该测量矩阵上的线性投影y∈RM定义为式(4)，其中Θ=ΦΨ为M×N的传感矩阵。

压缩感知的最终目的是重构原始信号x，但由于结构健康监测中的采样信号x自身不是稀疏的，从y重构原信号x的问题无法直接求解。这样就由原来的在测量矩阵Φ下，从y重构原信号x的问题;转换成在Θ矩阵下，从y重构稀疏系数α的问题。

根据Candes等人的研究，当M≥O(K·ln(N))且测量矩阵 Θ 满足 RIP约束等距性条件［16－17］时，稀疏系数α可通过测量值y求解l0范数的问题得到 α 的精确重构［18］。

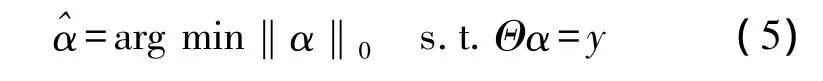
最终对^α在正交变换基Ψ重构可获得原始信号x的精确解^x，即:^x=Ψ^α。

在CS_WSN_SHM中构造测量矩阵时，主要思路就是寻找具有任意列向量构成的子集都具备近似正交性的测量矩阵，且这些子集越大越好，并且所选的测量矩阵Φ与正交基矩阵Ψ之间具有最大的不相关性［19］。

由于随机矩阵与任何稀疏基都具有很大的不相干性，如戴琼海教授在文献［20］中指出，当Φ是由随机数生成的随机矩阵或将某个正交矩阵进行随机行列互换形成的随机矩阵，与任意给定的矩阵的不相干程度非常大。文献［18］则证明了当Φ是高斯随机矩阵时，矩阵Θ=ΦΨ能以较大概率满足约束等距性条件。因此随机矩阵，尤其是高斯随机矩阵，是本文CS_WSN_SHM中构造测量矩阵考虑的重点。

1.3 CS_WSN_SHM的信号重构算法

稀疏信号的重构算法是压缩传感理论的核心，信号重构问题可以通过求解最小l0范数问题加以解决。已有的求解l0范数问题的方法都能在信号重构中实现。对于信号的重构算法，主要分成3大类，分别为贪婪算法、凸优化算法［21］和统计优化算法［22］。

贪婪算法中典型的是匹配追踪MP(Matching Pursuit)算法［23］，重建实现简单且速度快。正交匹配追踪 OMP(Orthogonal Matching Pursuit)算法［24］是对MP算法的改进，其目的是得到采样信号在测量矩阵上的最优投影，以保证残差最小，能精确重构出采样信号。

本文在研究OMP算法的基础上，根据结构健康监测的实际需求，提出一种改进的门限正交匹配追踪算法TOMP(Threshold Orthogonal Matching Pursuit)，如表1所示，其中s为从Rd中任意选取稀疏度为K的信号，Φ为N×d维高斯随机矩阵。

表1 改进的正交匹配追踪(TOMP)算法

与原有的OMP算法基础相比，如表1中的步骤6所示，改进的算法增加了一个重构误差门限值δ，该阈值根据实际结构健康损伤检测的需求确定，本文中δ取值0.05，表示5%的重构误差。在其他压缩感知的应用领域，TOMP算法同样适用，但要根据不同的应用需求设置δ参数值。上述算法中信号重构时，每次重构迭代都通过阈值δ来比较重构结果与原始结果，如果‖rt‖2＜δ则停止重构，并跳转到第8步骤。这样在重构迭代过程中，如果达到要求则可提前结束，而无需迭代满K次。改进的OMP算法，在保持重构精度的同时，有效的提高了算法的收敛速度，提高了重构效率。

2 压缩感知在CS_WSN_SHM上的应用

在传统无线的结构健康监测(WSN_SHM)的信号采集中，如图2所示，传感器节点经过高速采样获取N维的原始信号x(n)后，一种办法是将原始数据直接传输汇聚给基站进行协同判别结构状态;另外一种办法是将采集的原始数据压缩后传输给解码端，解压后再对结构的状态进行识别。其缺点在于，信号仍然需要按照Naquist速率进行采样，采集系统成本巨大，并造成资源的浪费;数据经过变换和量化后，需要对变换系数进行编码存储，在基站的解码端要实现解码、反量化和反变换，增加了整个系统的成本和复杂度。

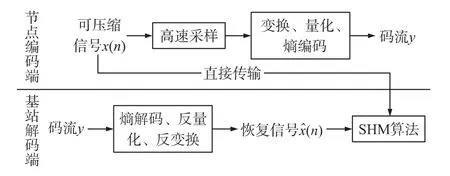
图2 WSN_SHM信号采集编码框架

基于压缩感知的结构监测数据采集中，如图3所示，该技术突破了传统的采样定律，它基于信号的稀疏先验，通过低速压缩采样的方式，以非自适应的随机投影获取少量的观测。其本质是采样和压缩的同时结合，减少了节点编码端的压缩过程，改为直接采集压缩数据，从而显著降低了采集系统的成本，最后在基站的通过求解合适的数值优化问题重构原始信号。从计算成本和能量消耗上来区分，传统的压缩技术是将计算成本和能量消耗平摊到节点编码端和基站的解码端;而压缩感知技术是将计算成本和能量消耗集中在具有高计算性能的基站解码端，节点的编码端几乎没有计算成本和能量消耗。

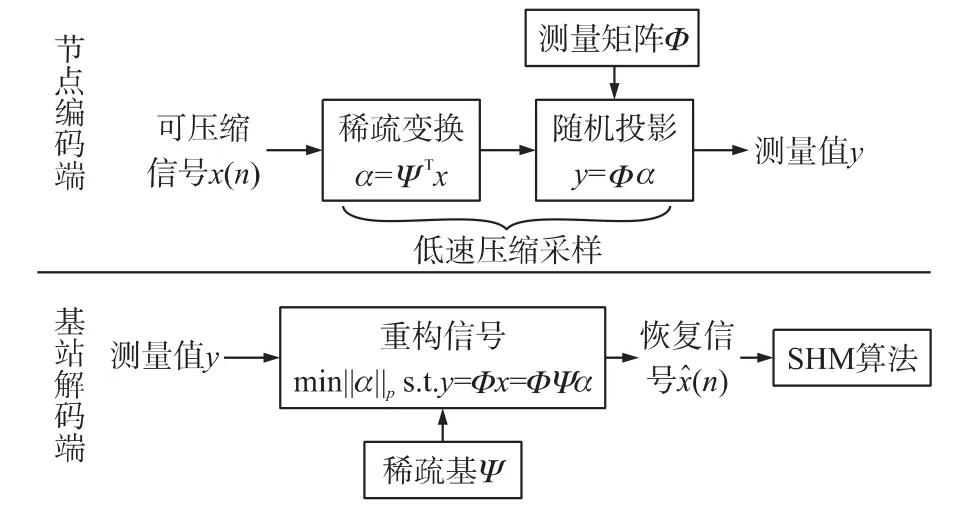
图3 CS_WSN_SHM的信号处理流程

图3中的编码端是指SHM中的每个传感器节点，N维的原始信号x(n)通过Ψ的稀疏变换后转换成N维的稀疏系数α(n)，经过M×N维的测量矩阵Φ随机投影后得到M(M≪N)维的测量值y(n)，通过从N维到M维的降维处理，实现了数据的压缩。在编码端，压缩感知的关键就是构造合适的、便于硬件实现的测量矩阵Φ。图中的解码端是指无线传感器网络中的Sink节点或者基站，基站在接收到测量值后，在稀疏基Ψ满足RIP的约束条件下，通过求解l0或l1范数的问题来精确重构原始信号，进而实现结构监测的SHM算法。

在本文中，将针对基于压缩感知的无线传感结构健康监测系统(图4)，采集稀疏测量值，实现信号的精确重构。并与传统的WSN_SHM的系统的采样信号对比，分析信号的压缩比和重构误差;并通过一种SHM检测算法实现结构损失识别，验证压缩感知的信号采集的有效性。

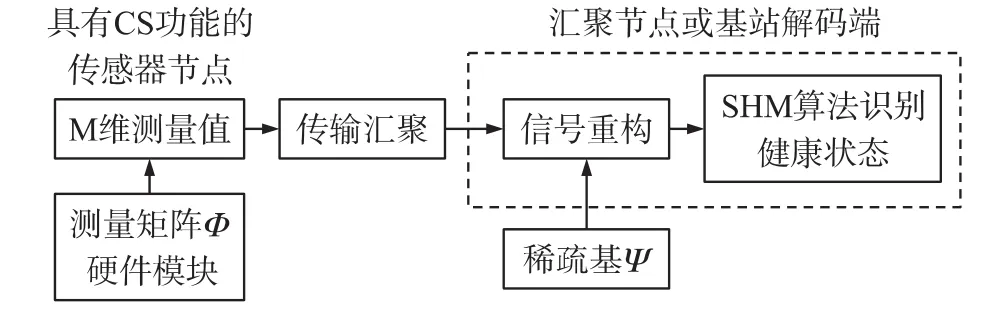
图4 CS_WSN_SHM的信号采集恢复框架

3 CS_WSN_SHM的实验验证

在本文实验中，设计了一个实验的SHM数据采集系统，分别布置普通传感节点(WSN_SHM)和具有压缩感知功能的传感器节点(CS_WSN_SHM)，实验系统由PXI数据采集系统、YE5850电荷放大器、KH7602宽带功率放大器以及粘贴了压电片的LF－21M防锈航空铝板组成。粘贴压电片的铝板结构示意图，如图5所示，LF－21M防锈铝板的基本尺寸为1 200×2 000×1.5(单位:mm)，8 个压电片的直径为Ф8 mm，厚度为0.2 mm，相邻两个压电片的中心间距为12 mm，8个压电片的标号从下而上依次为0～7号。图中标记Ф20 mm的圆为质量为10 kg的铁块加载位置，用于模拟结构部件的损伤位置。

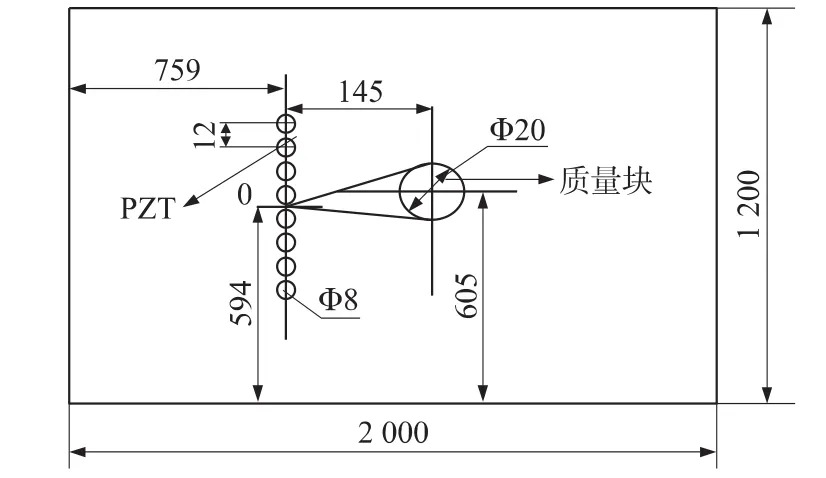
图5 实验试件的结构示意图

数据采集系统汇总，用于采集监测信号的数据采集系统PXI的最大采样频率为10 MHz，此次实验的采样频率为1 MHz，采集点数为1 024个。驱动器所激励的监测信号为窄带调制正弦信号，其中心频率为40 kHz，幅值为±10 V，波峰数为5。数据采集过程中，以轮循的方式进行数据采集，将阵列中的8个压电片分别作为驱动器，当其中一个作为驱动器时，其他的7个则作为传感器接收传感信号，每个接受传感器分别采集其0°～180°方向上的数据，共181次;这样可以采集7×8×181=10 136个传感信号，其中每个传感信号的采集点数为1 024个。

3.1 实验结果的评价标准

使用压缩感知的理论对SHM的信号进行数据压缩时，采用如下两种评价标准，分别为压缩比CR和重构误差ξ。

压缩比CR:是衡量数据压缩程度的指标之一，压缩比定义为原始信号数据量与压缩后信号数据量之比，如式(6)所示，No，Nco分别表示原始信号数据量和压缩后信号数据量。

重构误差ξ:反映对原始信号重构后的相似程度，是衡量数据解压缩后重构效果的重要指标，如式(7)所示，x分别表示重构之后的信号和原始信号。

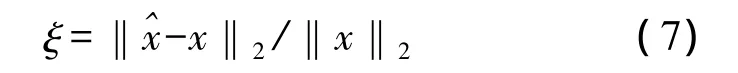
3.2 实验结果分析

实验中，分别对WSN_SHM和CS_WSN_SHM两种结构进行信号采集，采集的信号长度N=1 024。对压缩感知的采集系统进行信号重构，重构信号与原始信号的误差分析如图6所示。CS_WSN_SHM系统中，测量矩阵选取高斯随机矩阵，变换基为Haar小波正交变换基，重构算法采用改进的正交匹配追踪算法(TOMP)。

图6 CS_WSN_SHM信号重构误差分析

为了分析CS_WSN_SHM系统在信号采集过程中噪声干扰对重构信号的影响，实验过程中人为添加了随机噪声x=x+0.26×rand n(size(x))。图7显示了噪声干扰下的信号重构的误差分析。

图7 CS_WSN_SHM对噪声信号的重构误差分析

图6是对不含噪声的CS_WSN_SHM的重构信号的误差分析，图中可以看出，M×1维线性测量信号，观测次数M=231，从而从N维降至M维，压缩比为1 024/231=4.432 9;信号重构时，重构信号的相对误差ξ=0.083 0;重构信号与原始信号的绝对误差在［0.3262，0.3038］范围内，如图 6(f)所示，80%以上的采样点，绝对误差分布在±0.13之间。

从实验结果看，对于不含噪声的原始信号，压缩感知技术能实现较高的压缩比，并能以非常高的精确度实现信号的重构。

图7是对含噪声的CS_WSN_SHM的重构信号的误差分析，从结果来看，M×1维线性测量信号，观测次数M=259，压缩比为 CR=1024/259=3.9537;信号重构时，重构信号的相对误差ξ=0.4583;重构信号与原始信号的绝对误差在［－0.8802～0.9543］范围内，大部分采样点，绝对误差分布在±0.4之间。

从实验结果可以看出，重构相对误差ξ=0.4583比前者扩大了5.5倍，其原因在于CS_WSN_SHM对于含有噪声的采样信号，具有较好的抗干扰性。重构之后的结果更加接近于去噪声之后的原始信号。

3.3 基于CS_WSN_SHM的损伤识别验证

为了验证将压缩感知应用于无线传感结构健康监测领域的有效性，此处将采用我们已有的相控阵识别损伤［25］的研究成果，在CS_WSN_SHM环境下对实验中的铝板损伤进行损伤识别和定位。

利用压缩感知采集的0°～180°方向上的线性测量信号，通过信号重构后，把0°～180°范围内合成的信号，依据相控阵进行损伤识别的原理［25］，即按照其对应的角度和每个角度上信号相对应的幅值用灰度的形式画在同一个图上得到损伤图像，如图8所示，图中横，纵坐标代表位置，每点的灰度代表该点信号的幅度，灰度从暗到亮对应着能量从低到高，在损伤图像中损伤处显示高亮，图中用圆圈表示。其中，损伤中心点的位置为:(154.3 mm，91°)，与实际点(145.4 mm，94°)的误差为 8.4 mm，而且整个损伤均被检测出来。同样损伤检测方法在WSN_SHM环境下，误差为8.2 mm，可见基于CS_WSN_SHM的信号重构后的损伤检测是有效的。

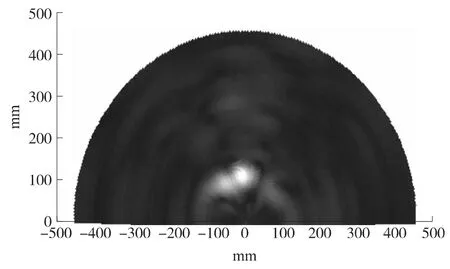
图8 CS_WSN_SHM中相控阵技术的损伤识图像

4 结论

结构健康监测是无线传感网的一个重要研究领域，压缩感知理论的应用能实现信号的压缩采样，节省网络传输的能量，提高系统的整体性能。本文在分析信号稀释化表示、测量矩阵选择等压缩感知理论的基础上，提出了基于压缩感知的无线传感结构健康监测方法CS_WSN_SHM，通过改进的信号重构算法，对航空结构材料的损伤进行识别定位。与已有的WSN_SHM相比，能实现数据压缩，减少网络的能耗。实验结果可以看出，CS_WSN_SHM方法不但能精确重构压缩采样信号，对噪声信号也具有较好的抗噪性，使得系统高效运行的同时也保证了材料结构损伤识别的精度。下一步拟研究其他结构健康监测的传感器信号(应变、位移和加速度等)的稀疏性及对应的正交基，并进一步优化重构算法以提高结构损伤识别能力。

［1］ Zhang Y，Li J.Wavelet-Based Vibration Sensor Data Compression Technique for Civil Infrastructure Condition Monitoring［J］.Journal of Computing in Civil Engineering.2006，20(6):390－399.

［2］ Zhang Y，Li J.Efficient Seismic Response Data Storage and Transmission Using ARX Model-Based Sensor Data Compression Algorithm［J］.Earthquake Engineering and Structural Dynamics.2006，35(6):781－788.

［3］ Chintalapudi K K.Design of Wireless Sensor Network Based Structural Health Monitoring Systems［D］.Los Angeles:Univ of Southern California，2006.

［4］ Zhang Y F，Li J.Linear Predietor-Based Lossless Compression of Vibration Sensor Data:Systems Approach［J］.ASCE Journal of Engineering Mechanies，2007，133(4):431－441.

［5］ 唐亮，周正，石磊.基于能量均衡的无线传感器网络压缩感知算法［J］.电子与信息学报，2011，33(8):1919－1923.

［6］ 蒋文贤.压缩感知的能量异构WSN分簇路由协议［J］.传感技术学报，2013，26(6):894－900.

［7］ 刘亚，刘功亮，康文静.压缩感知和LEACH结合的水下传感器网络信息采集方案［J］.传感技术学报，2013，26(3):388－395.

［8］ 余恺，李元实，王智，等.基于压缩感知的新型声信号采集方法［J］.仪器仪表学报，2012，33(1):105－112.

［9］ 邹志强，王悦，沙超，等.无线传感器水下监测网络稀疏采样和近似重构［J］.仪器仪表学报，2012，33(12):2728－2734.

［10］ Ma J，Hussaini M Y.Extensions of Compressed Imaging:Flying Sensor，Coded Mask，and Fast Decoding［J］.IEEE T Instrum Meas，2011，60(9):3128－3139.

［11］ Morlier J，Bettebghor D.Compressed Sensing Applied to Mode Shapes Reconstruction［C］//IMAC Conference and Exposition on Structural Dynamics.Jacksonville，USA，2012.

［12］ Cortial J，Farhat C，Guibas L，et al.Compressed Sensing and Time-Parallel Reduced-Order Modeling for Structural Health Monitoring Using a DDDAS［C］//IEEE Int Conf Computational Science(ICCS))，2007，Beijing，China.1171－1179.

［13］ Huang Y，Beck J L，Wu S，et al.Robust Diagnostics for Bayesian Compressive Sensing Technique in Structural Health Monitoring［J］.Structural Health Monitoring(SHM)，2011，1(2):103－110.

［14］ Yang Y C，Satish N.Structural Damage Identification Via a Combination of Blind Feature Extraction and Sparse Representation Classification［EB/OL］.Mechanical Systems and Signal Processing，A-vailable online 31 October 2013.

［15］鲍跃全.结构健康监测的数据压缩采样与损伤识别融合方法［D］.哈尔滨:哈尔滨工业大学土木工程学院，2009.

［16］ Candès E，TAO T.Near Optimal Signal Recovery from Random Projections:Universal Encoding Strategies［J］.IEEE Transactions on Information Theory，2006，52(12):5406－5425.

［17］ Candès E，Tao T.Decoding by Linear Programming［J］.IEEE Transactions on Information Theory，2005，51(12):4203－4215.

［18］ Candès E，Romberg J，Tao T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information［J］.IEEE Transactions on Information Theory，2006，52(2):489－509.

［19］ Baraniuk R G.Compressive Sensing［J］.IEEE Signal Processing Magazine，2007，24(4):118－121.

［20］戴琼海，付长军，季向阳.压缩感知研究［J］.计算机学报，2011，34(3):425－434.

［21］ Chen S S，Donoho D L，Saunders M A.Atomic Decomposition by Basis Pursuit［J］.SIAM Journal on Scientific Computing，2001，43(1):129－159.

［22］ Ji S，Xue Y，Carin L，et al.Bayesian Compressive Sensing［J］.IEEE Transactions on Signal Processing，2008，56(6):2346－2356.

［23］ Mallat S，Zhang Z.Matching Pursuits with Time-Frequency Dictionaries［J］.IEEE Transactions on Signal Processing，1993，41(12):3397－3415.

［24］刘冰，付平，孟升卫.基于正交匹配追踪的压缩感知信号检测算法［J］.仪器仪表学报，2010，31(9):1959－1964.

［25］孙亚杰.基于超声相控阵原理的结构健康监测技术研究［D］.南京:南京航空航天大学，2010.