基于GO法汽车制动系统可靠性研究*

贺 帅，杨建伟

(1.太原科技大学机械工程学院 山西 太原 030024;2.北京建筑工程学院机电与汽车工程学院北京 100044)

1 引言

随着汽车工业和人民生活水平的不断提高，汽车保有量迅猛增长。汽车结构日益复杂造成维修任务也随之增加，各种安全事故随之逐年增加，汽车安全性意识引起越来越多人重视，而汽车制动系统直接影响着汽车行驶安全性和停驻车可靠性，因此汽车制动系统的可靠性研究至关重要。

2 GO法分析

GO法是一种以成功为导向的系统概率分析技术，有其自身的特点，对于多状态、有时序系统，尤其是对有实际物流如液流、气流、电流的生产过程安全性分析更合适［1］。因此，研究 GO法理论和应用具有重要的理论意义和实用价值。

GO法可以将系统原理图、流程图或工程图直接按规则翻译成GO图。而GO图中操作符代表具体部件如安全阀、开关等，或代表部件间逻辑关系，信号流连接操作符，代表具体物流或代表逻辑上的进程。建立GO图后，通过输入操作符数据，按照操作符运算规则即可进行GO运算，从输入操作符输出信号开始，依照下一个操作符的运算符的规则依次进行计算，最后即可得到输出信号的状态和概率。

GO运算分为定性运算和定量运算。定性运算是按操作符规则，逐步分析各输入信号状态和单位状态组合，得到系统各状态的所有可能状态组合，即可找出路集和割集。定量运算是指通过分析每一个操作符的输入信号装填和单元组合得到输出信号状态时，计算状态概率，逐步计算得到系统的输出信号的状态概率［2］。GO法原理如图1所示。

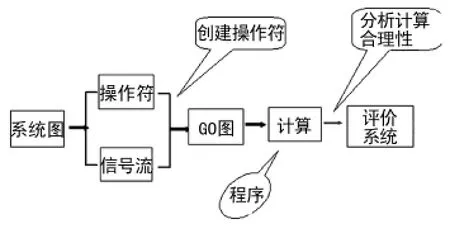
图1 GO法原理图

GO法有以下优点:①直接模拟系统，操作符和系统部件一一对应;②以成功为导向直接进行系统成功概率分析，和常规的工程分析、正常的流动过程分析相似，比较容易理解;③分析系统和部件故障状态的概率，操作符和信号流可表示多个状态;④可描述系统和部件在各个时间点的状态和状态的变化，可用于有时序的系统概率分析;⑤求系统成功的路集和系统故障的割集［3］。

3 汽车制动系统GO法分析

通过分析GO法基本原理和步骤，以某型汽车的单管路制动系统为例进行分析。单管路制动系统结构简单、成本低，制动系统良好［4］。但当系统管路出现故障时安全可靠性不高，影响车辆的制动性能。

单管路制动系统依靠手制动软轴拉动变速器输出轴上的制动鼓实现制动功能，制动原理如图2。汽车发动机带动空压机，空压机将压缩空气经卸荷阀调压进入储气筒，调压后压力值在 0.67～0.70 MPa。气体从储气筒出来后经由单腔制动总阀进入制动腔。当驾驶员踩下制动踏板时，气体由制动总阀分两路进入前后加力器，高压制动液经管道进入钳盘式制动器分泵，从而推动活塞将摩擦片与制动盘压紧实现制动。同时另一路通往前加力器的压缩空气通往变速器切断阀，切断动力［5］。

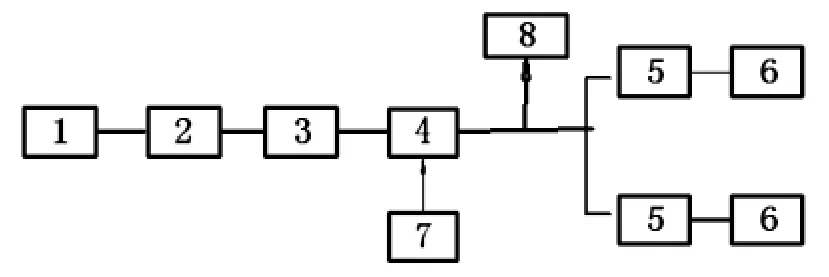
图2 制动系统原理图

按照规则将原理图翻译成GO图，其中空压机、制动踏板是系统的输入信号，包括成功和故障两个状态，用类型5表示。制动总阀用类型6表示，其余用类型1表示。制动总阀出来的气体经由两路通往前后制动加力器，增加一个逻辑操作符与门。系统GO图如图3所示。

图3 制动系统GO图

根据标准操作符类型的定义和运算规则，应用状态累计概率公式，推导出文中所能应用到的操作符状态累计概率计算公式。

(1)类型1两状态单元

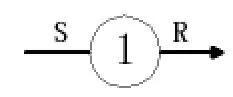
S为输入信号;R为输出信号输出信号状态概率计算公式为:

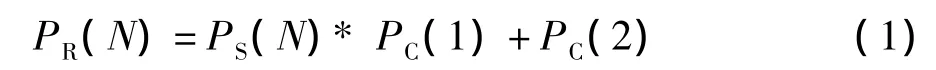
按状态累积概率定义，可得到状态概率累积概率计算公式:

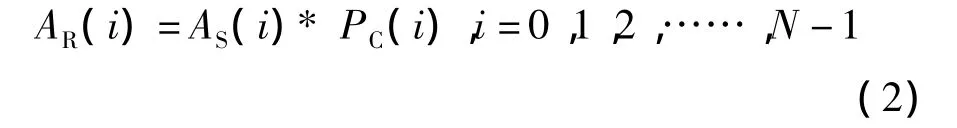
(2)类型5信号发生器

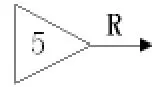
R为输出信号。

输出信号状态概率计算公式为:

输出信号状态概率累积概率计算公式:

(3)类型6有动作信号而导通的元件

S1为主输入信号;S2为次输入信号;R为输出信号。

输出信号状态概率累积概率计算公式:

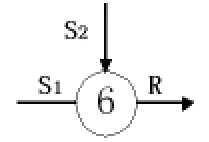
经推导知系统可靠度计算公式:

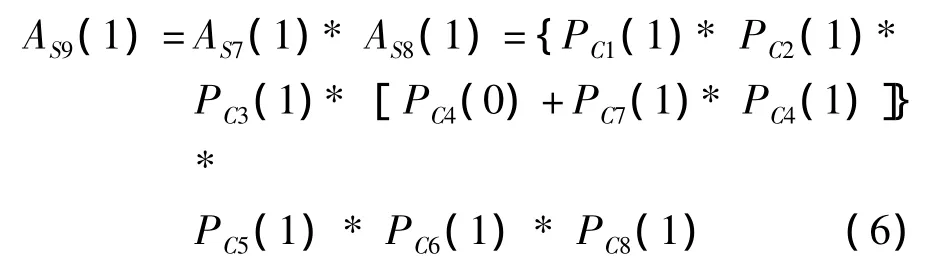
通过定量计算可对系统进行定性分析。可以计算出各部件在系统中的重要度。由定量计算可知，系统中单腔气制动总阀为三状态单元，一阶割集为除部件制动踏板外其他部件，制动踏板一阶计算近似为0，故可作为一阶割集。

4 可靠性评估软件编制

按各类型操作符的定义和运算规则，采用信号流状态累积概率和操作符的状态累积计算公式依次进行GO定量计算［6］。为方便计算，基于 VC++6.0环境下，创建对话框资源并创建对话框类的及连接，并为对话框类添加成员变量，通过建立资源对象和消息处理函数间的关系，完善消息响应函数主体代码的编写，编制制动系统评估软件［7］。图4为GO法可靠性分析软件的总体框图，图5为编制可靠性评估软件对话框界面。

输入各操作符的状态概率，设PCj(1)为编号j的累计概率。点击OK按钮运行软件，计算得到制动系统可靠度约为0.9044。操作度成功概率，ASi(1)为编号i的信号流成功状态

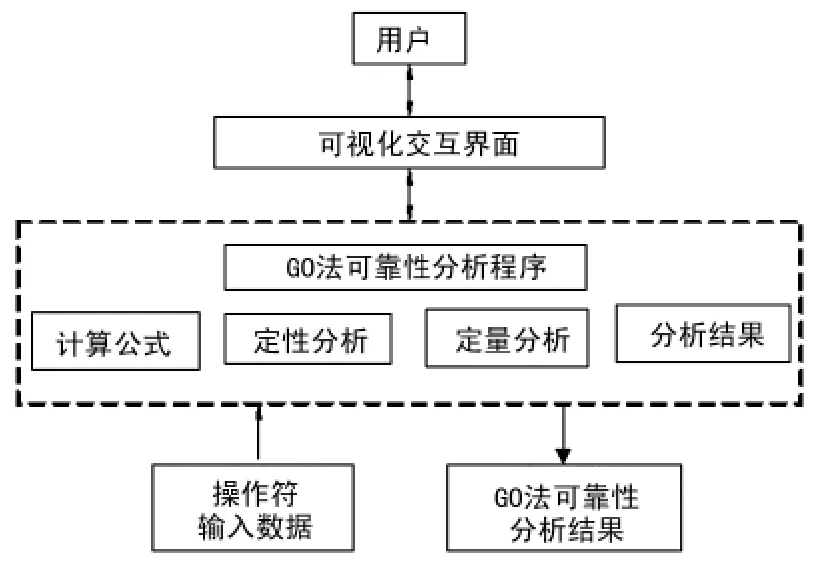
图4 GO法可靠性分析软件的总体框图

图5 编制可靠性评估软件界面

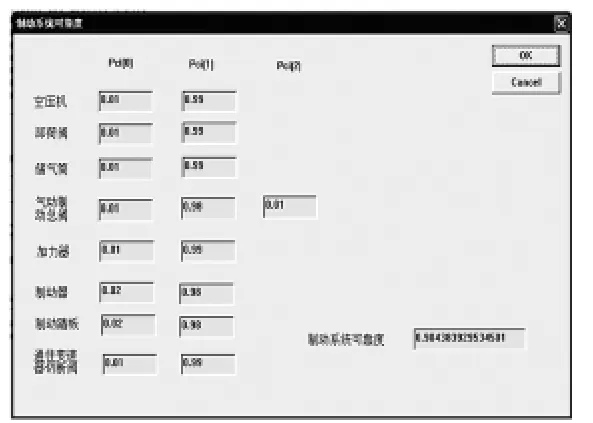
图6 制动系统可靠度分析界面

5 结论

通过分析可知，根据车辆制动系统组成单位的功能关系可得到系统的可靠逻辑框图，依照规则可推导出计算系统可靠度的关系式。若在各单元可靠度已知的条件下，即可计算出整个制动系统的可靠度。

对于复杂的系统，GO运算的状态组合庞大，经过验证状态累积概率定量计算结果和状态组合计算所得到的结果完全一致。而状态累积概率计算可避免繁琐的状态组合和复杂的定性分析过程，应用公式计算直接得到信号流状态概率，使GO法的优点更明显。通过编制软件，对复杂系统，可直接、快速地得到系统信号流的状态概率，完成定量计算过程，提高可靠性评估的效率。对研究汽车制动系统的安全可靠性有重要作用。

［1］沈祖培.复杂系统可靠性的GO法确算法［J］.清华大学学报，2002，42(5):569 －572.

［2］沈祖培，黄祥瑞.GO法原理及应用［M］.北京:清华大学出版社，2004.

［3］林 洁.GO－FLOW原理及其计算机辅助技术［D］.北京:国防科学技术大学，2003.

［4］何宇漾.基于神经网络的汽车制动系可靠性分析［J］.湖北汽车工业学院学报，2005(3):14－16.

［5］阮社楼.汽车制动系可靠性分析［J］.设计与计算，2003(1):29－30.

［6］王育坚.Visual C++面向对象编程教程［M］.北京:清华大学出版社，2003.

［7］春 葆.C++语言程序设计导学［M］.北京:清华大学出版社，2002.