某型汽车驱动盘轴向冲击疲劳计算分析*

杨毅超，张大可，刘 路

(重庆大学机械工程学院，重庆 400044)

1 引言

汽车驱动盘用于连接汽车发动机曲轴和自动变速器(AT)的液力变矩器，是汽车传动系统中的重要零部件之一［1］。汽车驱动盘通常由驱动盘盘体和启动齿圈组成，二者通过沿盘体外缘呈圆周对称分布的偶数段焊缝相互连接，其基本结构如图1所示。驱动盘盘体中心孔附近设计有与发动机曲轴连接的螺栓孔，盘体外圈附近有与液力变矩器连接的螺栓孔，减重孔均布于盘面上，用来减轻盘体质量从而降低驱动盘的转动惯量，提高传动效率。汽车驱动盘的主要作用为传递发动机扭矩，并在起动电机的带动下起动发动机。汽车启动时，起动电动机轴上的齿轮驱动启动齿圈，载荷作用于齿圈顶部，通过驱动盘盘体与曲轴的连接起动发动机;行驶状态下，动力由发动机曲轴传递到驱动盘盘体，再由盘体经液力变矩器传出。

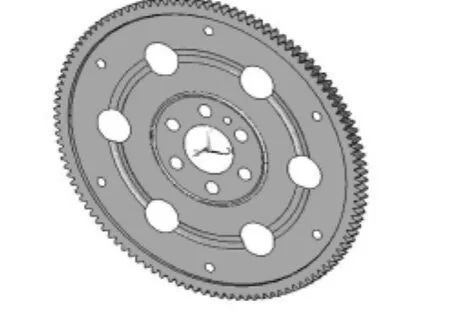
某型汽车驱动盘三维实体结构图

汽车驱动盘承受的载荷主要是发动机扭矩，但其在工作过程中不可避免地承受其他载荷作用。由于与其相关联部件的轴向窜动，驱动盘将承受轴向载荷作用，有可能引起疲劳破坏。因此轴向冲击引起的疲劳是设计考量的重要指标之一。由于计算的复杂性，工程实际中多是根据所使用的材料性能从理论上估算驱动盘的疲劳寿命，获得的结果精度不高。采用疲劳试验的方法获得疲劳寿命是较为可靠的方法，但产品开发周期长，设计成本高。因此，对汽车驱动盘进行疲劳仿真分析具有很大的实用价值。

2 ANSYS有限元软件疲劳分析的理论基础

ANSYS疲劳计算是以ASME锅炉与压力容器规范作为计算依据，采用简化了的弹塑性假设和Miner累积疲劳准则来估算零件的疲劳寿命［2］。

2.1 材料的疲劳特性

材料在循环应力或循环应变的作用下，由于某点或某些点产生了局部的永久结构变化，从而在一定的循环次数以后形成裂纹或发生断裂的过程叫做疲劳［3］。反映材料疲劳强度的特性曲线为S－N曲线，即交变应力强度(σmax－σmin)/2和允许循环次数的曲线。本驱动盘盘体的材料为QSTE380，其强度极限σb=590 MPa，屈服极限为σs=380 MPa。由于缺乏材料的疲劳试验数据，本文采用近似方法估计其S－N曲线，根据陈传尧［4］推荐，材料循环次数 N=103时，材料疲劳极限为90%σb，N=107时，材料疲劳极限为50%σb。由式(1)、(2)可得到材料的近似S－N曲线，如图2所示。

式中:N为材料循环次数;S为应力值;单位为MPa;m和C是与材料、应力比、加载方式有关的参数。

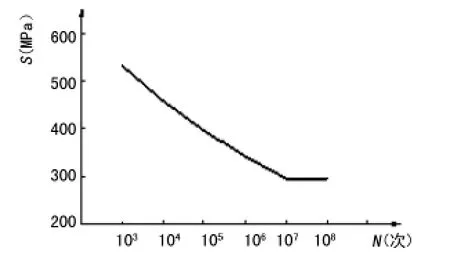
图2 材料QSTE380的S－N曲线

2.2 Miner准则

ANSYS－Fatigue模块计算疲劳损伤系数采用工程上广泛使用的Miner线性疲劳累积损伤理论。其计算公式为:

式中:Ni为对应于当前载荷水平Si的疲劳寿命;n为循环次数;D为疲劳损伤系数。

根据ANSYS计算出的疲劳损伤系数来判断材料是否满足疲劳强度要求，当D＜1时，认为材料不会发生疲劳破坏，当D=1时，材料处于疲劳临界状态，当D＞1时，认为材料已经发生疲劳破坏。

3 基于ANSYS的疲劳分析

3.1 建立有限元模型

3.1.1 建立几何模型

在汽车驱动盘受到轴向冲击时，主要由驱动盘盘体抵抗冲击，启动齿圈并不参与工作，因此在进行疲劳有限元分析时，模型不含齿圈。该驱动盘盘体由2.5 mm薄钢板冲压而成，盘面不在同一个平面内，盘面上开有减重孔和各种螺栓通孔，结构较为简单，无需对结构做简化处理。以盘体的中性面为基准面建立驱动盘盘体的几何模型，模型如图3。

3.1.2 材料物理参数

驱动盘盘体材料为QSTE380，其弹性模量为E=2.06 ×105N/mm2，泊松比 μ =0.29，密度为 ρ=7.8 ×10－6kg/mm3。

3.1.3 单元选择与网格划分

由于该驱动盘盘体厚度仅为2.5 mm，受盘体面内载荷作用，宜选用SHELL93单元，SHELL93为8节点弹性壳单元，含有中间节点，每个节点有6个自由度，即沿节点坐标系x、y和z方向的平动位移和绕各轴的转动位移，单元在面内各方向具有二次形函数，能够很好地模拟盘体的几何和载荷特征。划分网格后的有限元模型含有壳单元5703个，节点17776个。

3.1.4 载荷与约束处理

驱动盘与曲轴连接处有6个螺栓孔，通过卡盘将驱动盘夹紧于曲轴上。当螺栓拧紧时，认为盘体螺栓孔所在的圆环面与曲轴无任何相对运动。这是保持驱动盘静定的静力学条件。为此将该接触面积处理为全约束，即约束x、y、z方向的平动与转动自由度。驱动盘与液力变矩器连接孔为载荷作用处，为模拟驱动盘受到的轴向冲击，按设计参数，在驱动盘盘体与液力变矩器连接孔分布圆周外施加+/－0.5 mm轴向(Z向)位移载荷。其载荷与约束处理的有限元模型如图4所示。

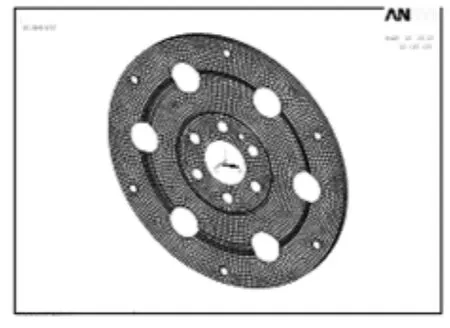
图3 某型驱动盘盘体有限元模型

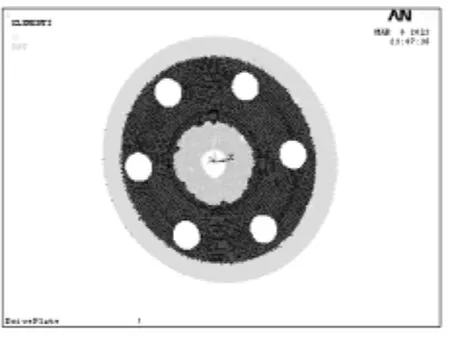
图4 某型驱动盘盘体约 束与载荷图

3.2 静力分析

分别施加+/－0.5 mm轴向位移载荷时驱动盘盘体的应力分布如图5、图6所示，由应力云图可知应力最大点的位置均为驱动盘与曲轴连接的螺栓孔附近，同时也是盘面圆弧曲率发生变化的位置，最大应力值约为269 MPa，远小于材料的屈服极限380 MPa，肯定不会发生盘体结构的强度破坏，满足结构的静强度要求。

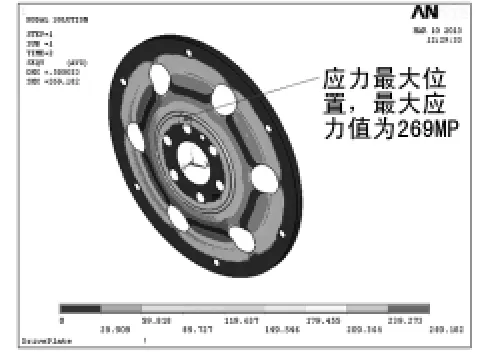
图5 驱动盘承受+0.5 mm 轴向位移载荷应力 分布云图

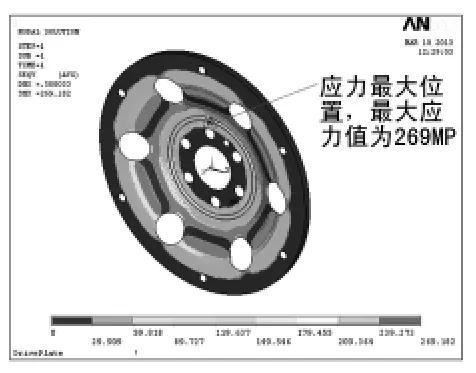
图6 驱动盘承受－0.5 mm轴向位移载荷应力 分布云图

3.3 疲劳分析

驱动盘承受单向0.5 mm或－0.5 mm轴向位移载荷时，冲击为脉动循环。若承受+0.5 mm轴向位移再接－0.5 mm轴向位移冲击，则为对称循环。这里的疲劳计算以最不利的对称循环应力组合进行计算，其应力幅值为脉动循环时的2倍。根据静力学分析结果，选择应力最大位置的9163号节点作为疲劳分析对象。设计要求驱动盘盘体应满足107次的单向0.5 mm的轴向冲击。故应力循环次数设定为5×106，计算结果如图7，疲劳损伤系数为0.87029，小于1，能够满足疲劳强度要求。

图7 ANSYS疲劳分析计算结果

为了便于设计分析，本文将对称应力循环下，不同轴向冲击位移值载荷下的疲劳损伤系数列于表1，由表1可知该型驱动盘盘体在承受+/－0.51 mm轴向冲击位移载荷时的疲劳损伤系数为1.19213，大于1，但考虑到本文采用的是最不利的应力循环方式，可以认为该位移值载荷冲击下，盘体处于疲劳破坏的临界状态。但若冲击位移大于+/－0.51 mm，则驱动盘将产生疲劳破坏。

表1 不同轴向冲击位移下的疲劳损伤系数

4 结论

本文利用ANSYS软件建立了某型汽车驱动盘的有限元模型，对驱动盘盘体作了+/－0.5 mm轴向冲击载荷条件的疲劳仿真分析。分析表明，该盘体满足结构的静强度要求，其疲劳损伤系数为0.8075，满足疲劳强度设计要求。同时，利用原有模型，对其他较大的冲击载荷作了疲劳仿真对比，获得该驱动盘不产生疲劳破坏的轴向冲击极值。采用本文方法可以缩短新产品的设计周期，节约产品开发成本，为其它零部件的疲劳分析提供了一定参考价值。

［1］ZHANG Da － ke，WANG Chong，YANG Yi－ chao，et al.The layout optimization for axial stiffness of a flexplate disk with weight and inertial moment constraints［J］.Advan － ced Materials Research，2013(2):630－635.

［2］曾 攀，雷丽萍.基于ANSYS平台有限元分析手册［M］.北京:机械工业出版社，2010.

［3］李舜酩.机械疲劳与可靠性设计［M］.北京:科学出版社，2006.

［4］陈传尧.疲劳与断裂［M］.武汉:华中科技大学出版社，2002.