基于ANSYS的航空发动机测量耙模态分析法*

陶 冶，田 琳，张永峰

(中国飞行试验研究院，陕西 西安 710089)

1 引言

采用测量耙/测头测量航空发动机各截面的压力和温度，是发动机定型试飞中的主要测量手段之一［1］。发动机试验时，在相关气流流通壁面上安装温度和压力测量耙或测头，如果测量耙或测头的固有频率与发动机的振动或气流激励频率相吻合，会产生谐共振，使测量耙或测头容易损伤甚至断裂。轻者测量耙或测头不能正常工作，重者将损伤发动机转动部件，危及飞行安全。由于航空发动机测量耙主要受气流载荷和振动载荷作用，在进行测量耙设计时，气流载荷相对较小，静强度要求能得到满足。因此，为确保测量耙/测头安全工作，必须进行测量耙模态分析和试验［2］。

测量耙模态设计方法一般分为试验法和有限元分析法:①试验法，即根据工程经验，预先设计出测量耙，加工后进行模态试验。如果试验结果发现测量耙固有频率远离发动机各种转子部件激励频率，那么该测量耙可直接投入使用;如果试验结果表明测量耙固有频率和发动机某转子部件激振频率重合或者比较接近，那么就需要修改设计，再进行试验直至得到符合要求的测量耙;②有限元分析法，是引入有限元技术以后产生的新方法。即采用有限元计算软件(如ANSYS等)［3］，根据设计尺寸建立三维模型，进行有限元模态分析，直接得出测量耙的固有频率。然后将分析结果与发动机各转子部件激励频率进行比对，如果比较接近，那么就就需要修改该测量耙的尺寸参数，再进行有限元分析，直至得到符合要求的测量耙，确定最终的测量耙尺寸设计参数［4］。

对测量耙的模态设计，早期均采用试验法，该方法可以解决问题，但有如下缺点:

(1)设计尺寸选择缺乏定量理论依据，只能根据工程经验，对设计人员工程经验要求比较高。

(2)设计完成后直接进行模态试验，一旦发现固有频率与激励频率重合或接近，就需要重复设计过程，设计周期长，成本高。

近年来，多采用试验法和有限元分析法相结合的方法，即在进行模态试验前先进行有限元分析。在有限元分析得出的模态符合设计要求的前提下，加工相应的测量耙，进行试验验证。相比于试验法，这种方法有了很大的进步，不但大大降低了研制测量耙的难度和周期，也降低了研制成本，成功的弥补了试验法的缺陷。因此，有限元分析是新型测量耙研制的重要组成部分。

2 测量耙模态分析法

航空发动机测量耙主要由耙体、底座、测头和传感器引线(嵌于耙体内部)组成［5］，如图1所示。飞行条件下，测量耙承受拉压、弯扭和摩擦等各种力的作用，进行理论计算有相当大的难度。因此，在满足工程要求的前提下，有必要对测量耙的计算模型进行合理的简化，以减小计算量和计算时间。

图1 航空发动机测量耙

一般情况下，在对实际模型进行简化时，并不考虑因结构简化而引起的质量变化的影响［6］，这种简化计算方法称之为常规方法，这种模型就是常规模型。但是，当被简化掉的结构质量占实际模型总质量的比例较大时，常规方法计算得到的结果会产生较大误差。

由于传感器引线和测头的质量之和占测量耙总质量的比例较大，采用常规方法计算得到的结果误差较大。因此，在常规方法的基础上，提出了等效质量法，即基于ANSYS的航空发动机测量耙模态分析法。这种方法不但简化了测量耙模型的结构，还通过设定等效密度，使简化后的模型总质量较试验件不变，这样就得到了等效模型。选用求解速度快，精确度较高的Block Lanczos法特征值求解器［7］进行模态分析，进一步简化分析流程和减少计算时间，最终得出满足要求的结果。

基于ANSYS的航空发动机测量耙模态分析法共有以下几个主要步骤:

(1)建立三维实体模型时，去掉了测头和传感器引线，将测量耙结构简化成为由耙体和底座构成的简单模型。

(2)将简化的三维模型导入大型通用有限元分析软件ANSYS中，选用8节点四面体单元SOLID45，采用SMART3自由分网技术，在耙体与底座的连接部分对接合面和线进行网格加密处理，生成测量耙的三维有限元网格模型。

(3)定义测量耙材料参数，如弹性模量E和密度ρ(或者某种形式的质量)等模态分析必须定义的参数［8］。为了确保简化模型的有效性，应当计算等效密度，以保证有限元模型的质量与扫频振动试验时使用的测量耙试验件相同。相应的等效密度公式如下:

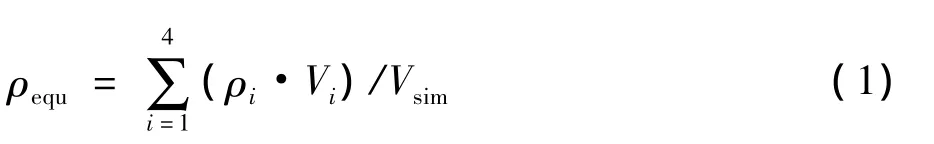
式中:ρequ是指等效密度;ρi是指测量耙试验件各组成部件的质量;Vi是指测量耙试验件各组成部件的体积;Vsim是指有限元模型总体积。

(4)根据试验时测量耙的安装方式，对有限元模型施加合理的位移约束。由于测量耙扫频振动试验时均采用螺栓连接安装，螺栓孔并未完全固支，如果对螺栓孔内壁面实行全方向位移约束，那么势必导致约束刚度过大，计算出的测量耙固有频率偏高的结果。因此，主要对螺栓孔上下圆线施加全方向位移约束，以尽量模拟实际情况下的安装方式。

(5)选用Block Lanczos法特征值求解器进行模态分析，因为这种求解器采用稀疏矩阵方程求解，求解速度快，且精确度较高。定义计算模态阶数，进行有限元模态分析，输出模态分析结果，并与测量耙扫频振动试验结果进行比对，验证所提测量耙模态分析法的可行性。

3 算例分析

对两种典型的航空发动机测量耙试验件进行了有限元模态分析，分别是某高压压气机进口总温总压测量耙(以下简称25耙)和某低压涡轮出口总温总压测量耙(以下简称50耙)，试验安装方式如图2所示，简化后的三维实体模型如图3所示，相应的有限元网格模型如图4所示。

图2 试验安装图

图3 测量耙简化模型图

图4 测量耙网格模型图

在频率范围为10～2000 Hz，以振幅0.3 mm(10～40 Hz)、加速度2 g(40 Hz以上)进行正弦扫频试验，以确定试验件在规定频率范围内的共振频率，在整个频率范围内均匀缓慢地改变激励频率，相应的扫频速率不大于每分钟一个倍频程，试验曲线见图5。

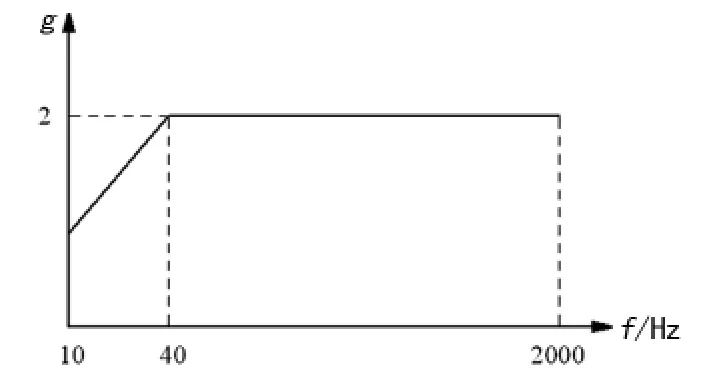
图5 扫频试验曲线

由于试验条件限制，主要考察一阶固有频率，相应的有限元分析结果与扫频试验结果的对比，见表1和表2所例。表1和表2中“X方向”是指沿测量耙测头进气方向，“Y方向”是指垂直进气方向，“Z方向”是指沿耙伸展的方向。

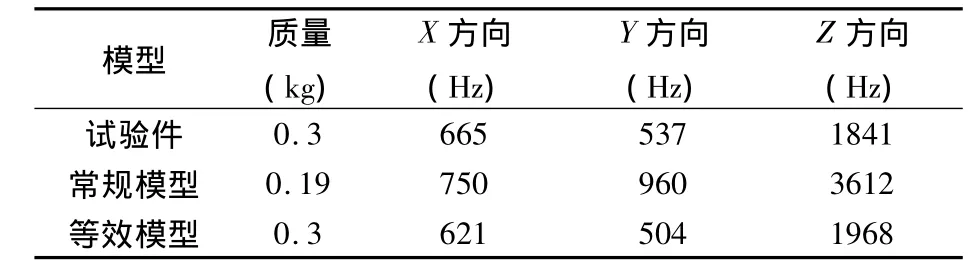
表1 25耙计算结果与试验结果对比表

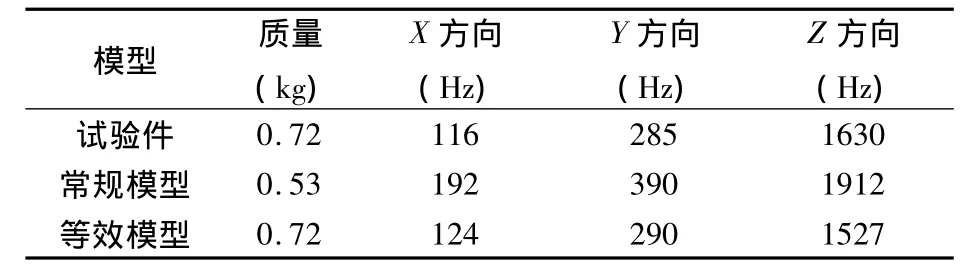
表2 50耙计算结果与试验结果对比表

从表1中数据可以看出，25耙常规模型X方向计算结果较试验件扫频试验结果的误差为12.8%，等效模型X方向计算结果较试验件扫频试验结果的误差则为6.6%;常规模型Y方向计算结果误差为78.8%，等效模型Y方向计算结果误差为6.1%;常规模型Z方向计算结果误差为96.2%，等效模型Z方向计算结果误差为6.9%。

从表2中数据可以看出，50耙常规模型X方向计算结果较试验件扫频试验结果的误差为65.5%，等效模型X方向计算结果较试验件扫频试验结果的误差则为6.9%;常规模型Y方向计算结果误差为36.8%，等效模型Y方向计算结果误差为1.8%;常规模型Z方向计算结果误差为17.3%，等效模型Z方向计算结果误差为6.3%。

4 结论

(1)从两种测量耙的有限元分析结果与试验件扫频试验数据的对比可以看出，采用基于ANSYS的航空发动机测量耙模态分析法的计算结果较试验件扫频试验结果的误差不超过7%，低于工程可接受的误差要求，说明了该方法的合理性。

(2)采用常规方法的计算结果较试验件扫频试验结果的误差均大于12%，甚至可达96.2%，超出工程可接受的误差要求，该模型不能正确反映试验件振动特性。因此，针对测量耙模型，常规方法光简化结构而不考虑质量变化对固有频率的影响不可行。

(3)新型测量耙研制时，预先对所设计的测量耙进行有限元分析，并由分析结果确定是否对初始设计进行改进，这样可避免设计过程中重复“设计－试验－改进”的反复工作，既能减小研制周期，又能降低研制成本。因此，基于ANSYS的航空发动机测量耙模态分析法为新型测量耙的设计改进提供重要手段。

［1］Yuhas A J，Ray R J，Burley R R，et al.Design and Development of an F/A－18 Inlet Distortion Rake:A Cost and Time Saving Solution［R］.NASA TM － 4722，1995.

［2］Amin N F，Hollweger D J.F/A － 18A Inlet/Engine Compatibility Flight Test Results［R］.AIAA 81 － 1393，1981.

［3］小飒工作室.最新经典ANSYS及ANSYS Workbench教程［M］.北京:电子工业出版社，2004.

［4］和永进，史建邦，邢 雁，等.某型飞机进气道测量耙研制［J］.燃气涡轮试验与研究，2008，21(3):59－62.

［5］陈 光.航空发动机结构设计分析［M］.北京:北京航空航天大学出版社，2006.

［6］张明旭，尹志宏，刘晓东，等.结构几何简化对模态结果的影响［J］.起重运输机械，2009(3):64 －65.

［7］张洪才，何 波.有限元分析——ANSYS 13.0从入门到实战［M］.北京:机械工业出版社，2011.

［8］博弈创作室.APDL参数化有限元分析技术及其应用实例［M］.北京:中国水利水电出版社，2004.