过盈配合面的接触刚度和接触阻尼计算研究

万俟昊天，向 阳，夏雪宝，刘 辉

(武汉理工大学 能源与动力工程学院，武汉430063)

过盈配合是机械工程中一种常见的构件连接方式，由于其配合连接紧密，可传递转矩，承受很大的轴向力，已广泛地应用于重型机械、起重运输机械、船舶、机车及通用机械中［1-2］。

过盈配合的过盈量大小是否对设备整体的动态特性有影响，以及有多大影响是本文研究的目的，特别是获得过盈配合结合面的特性参数(接触刚度和接触阻尼)。由于过盈配合结合面本身的结构特点(结合面为封闭结构，无法在结合面上布置传感器)，难以采用试验的方法直接识别结合面特性参数，所以这里采用有限元计算的方法，建立过盈配合组件的有限元模型，对模型施加一定的边界条件，仿真后提取结合面上单元和节点的接触压力、位移等参数，计算接触刚度和接触阻尼，最后再通过实验来验证结合面参数的正确性。

1 研究对象

研究对象为轴和轴套的过盈配合，见图1。轴和轴套材料为Q235，其几何尺寸和材料属性见表1。轴套内圆直径选择3种尺寸偏差:φ38--00..005716，φ38--00..003549，φ38--00..000383mm;与轴的尺寸偏差φ38-00.016mm配合，形成3种过盈量不同的配合形式，用代号表示分别为:U7/h6、S7/h6、N7/h6;其平均过盈量分别为:-0.055 5 mm、-0.038 5 mm、-0.012 5 mm。

图1 过盈配合示意

表1 过盈配合组件基本尺寸和材料属性

本文将过盈配合结合面特性参数定义为kyf、kym、kθf、kθm、cyf和cym［3］。见图2，对于过盈配合，在轴上施加y方向上的力f(t)，过盈配合结合面上沿z方向上任一点A产生位移y，此时这一点表现的刚度特性即为kyf，阻尼特性即为cyf;同样施加力f(t)，A点产生转动Δθ，此时这一点表现的刚度特性即为kθf。同理，施加力矩m(t)，A点产生位移y，此时这一点表现的刚度特性即为kym，阻尼特性即为cym;同样施加力矩m(t)，A点产生转动Δθ，此时这一点表现的刚度特性即为kθm。

图2 过盈配合结合面接触刚度及阻尼定义

2 接触刚度及接触阻尼有限元计算

根据轴和轴套尺寸属性在ANSYS中建立过盈配合的有限元模型。建立有限元模型时，为了减少单元数量，节约运算时间，将轴的长度设为200 mm。有限元模型中，轴和轴套采用SOLID186单元，共计5 610个;在轴和轴套配合的面上分别建立CONTA174单元和TARGE170单元(各816个)，形成接触对［4］。整个有限元模型共计26 464个节点。图3所示为所建的有限元模型:坐标原点位于轴孔配合端面中心处(图3所示坐标位置)，x轴为水平方向，y轴为竖直方向，z轴为轴和轴套的轴线方向。

图3 过盈配合有限元模型

进行有限元计算的时候，约束轴套端面外圆上面上下左右4个节点，见图3。仿真计算分两个时间步长完成(每个时间步长分别有5个子步)。在第一个时间步长中施加过盈量，轴孔配合面上的接触压力逐渐增大［5］。在第二个时间步长中，在轴的上端靠近轴孔配合处施加y轴负方向的力和力矩(见图3)。仿真计算中，力和力矩分10次施加:力为250～1 250 N，间隔250 N;力矩为2.5～12.5 Nm，间隔2.5 Nm。以力的施加为例，两个时间步长见图4。

图5所示为过盈配合U7/h6结合面上轴的上中心线沿z轴方向上的接触压力。可以看出从z=0 mm开始结合面上的接触压力逐渐增大，到大约z=50 mm附近接触压力达到最大，之后接触压力随着z的增大急剧下降。

2.1 接触刚度

图4 过盈配合有限元模型的载荷步长设置

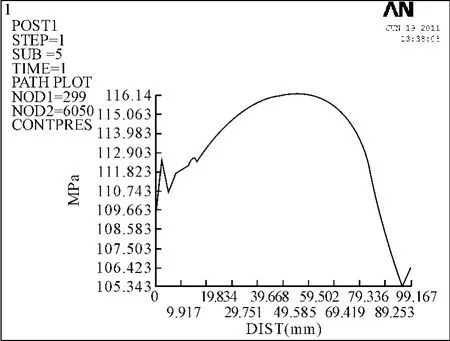
图5 过盈配合U7/h6结合面上沿z轴方向的接触压力

在第二个时间步长结束时，分别提取出在各个载荷下，轴的上中心线上沿z轴方向上各节点在y轴方向上的位移DOF-y。根据250～1 250 N载荷下的位移DOF-y，可以拟合出轴的上中心线上各个节点的载荷对位移的曲线，曲线的斜率即为kyf。同理，施加2.5～12.5 Nm的力矩可以得出kym。为了得到kθf和kθm，需要先得出轴的上中心线上的节点的转角θ。θ根据节点位移DOF-y，运用中心有限差分方法计算得到。从而可以拟合出轴的上中心线上各个节点的载荷对转角θ的曲线，曲线的斜率即为kθf和kθm。

图6所示为不同配合结合面上轴的上中心线沿z轴方向上的kyf。从图中可以看出，从z轴的0点位置开始kyf迅速增大，形成一个峰值，之后沿z轴方向呈下降趋势。图7所示为不同配合结合面上轴的上中心线沿z轴方向上的kym。从图中看出，在z=10 mm左右出现一个峰值，之后kym沿z轴方向呈下降趋势。图8、9所示分别为不同配合结合面上轴的上中心线沿z轴方向上的kθf和kθm。从图中可以看出，kθf和kθm沿z轴方向大体呈下降的趋势。同时，从各图中可以看出不同的过盈量对刚度值影响不大。

2.2 接触阻尼

图6 kyf

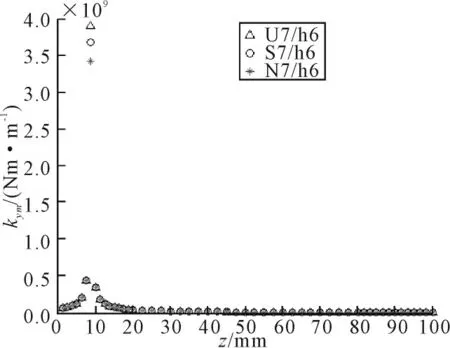
图7 kym

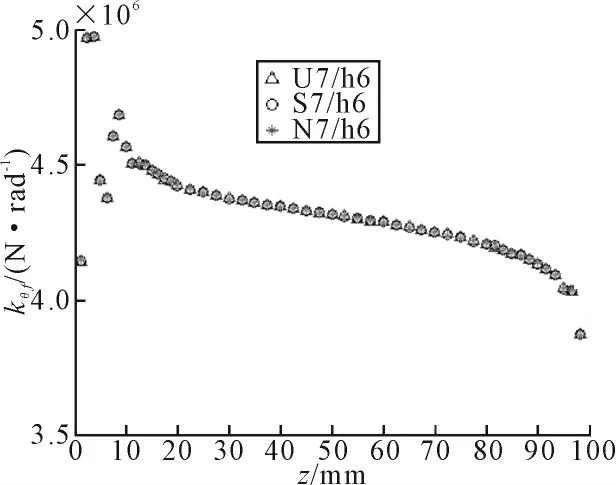
图8 kθf

图9 kθm

在向有限元模型施加载荷时，轴和轴套之间产生了微小的滑动，从而产生了能量损耗。这样，将轴和轴套之间沿z轴方向上各点的接触阻尼考虑为库仑阻尼［6］。从而，等效的粘性阻尼由式(1)计算得到:

式中:Fd，n——结合面上每一个接触单元的摩擦力，由单元面积乘以单元接触压力再乘以摩擦系数得到(见表1);

|zn|——结合面每一个接触单元沿z轴方向上滑动位移的绝对值;

ω——圆频率。

计算时将z轴方向上每一位置沿轴圆周方向一圈所有的单元的阻尼相加作为这一z轴位置上的阻尼。需要注意的是，在靠近中性轴处的单元的滑动几乎为0，这在使用式(1)计算等效阻尼时会得到很大的阻尼值。因为中性轴附近的微小滑动由几何约束造成，这些微小的滑动并不能够正确地表示阻尼的增加。因而中性轴附近内的单元不纳入等效阻尼计算。在第二个时间步长中，分别在每一个子步上计算等效阻尼ceq，n，再将计算结果相加，即得到在不同载荷下沿z轴各个位置上的接触阻尼cyf和cym。

图10和图11所示分别为配合U7/h6在施加500 N的力和12.5 Nm力矩时的接触阻尼值。从图中可以看出，cyfω和cymω的值沿z轴方向都比较离散。在z为20～30 mm处，cyfω值较大，其后呈下降的趋势。cymω在z为10～20 mm处形成峰值，之后沿z轴下降。

图10 U7/h6等效阻尼(500 N)

图11 U7/h6等效阻尼(12.5 Nm)

图12 和图13所示分别为配合U7/h6在施加不同力和力矩时的阻尼值。可以看出，在施加不同力(或者不同力矩)时，结合面上沿z轴的阻尼值呈现相同的趋势。图14和图15分别为不同过盈量的配合在施加500 N的力和12.5 Nm力矩时其结合面上的接触阻尼值。从图中可以看出，在过盈量不同时，结合面上沿z轴的阻尼值呈现相同的趋势。

图12 U7/h6等效阻尼cyfω

图13 U7/h6等效阻尼cymω

图14 不同配合cyfω(500 N)

3 实验验证

使用前文所述有限元仿真计算获得的接触刚度和接触阻尼数据，根据Euler-Bernoulli梁理论，运用结构响应耦合方法［7］，建立过盈配合的理论模型，计算过盈配合一端的频率响应函数，与实验测试的频率响应函数对比，验证接触刚度和接触阻尼的正确性。

图15 不同配合cymω(12.5 Nm)

3.1 背景介绍

Bishop和Johnson［8］提出了Euler-Bernoulli梁弯曲振动时频率响应函数的计算方法(见图16)，一两端自由的梁两端分别施加力f1(t)和f2(t)，以及力矩m1(t)和m2(t)，产生位移y1(t)和y2(t)，转角θ1(t)和θ2(t)。梁两端的原点和跨点频响函数分别为

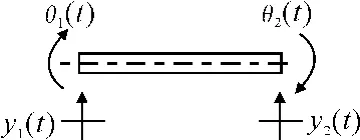
图16 两端自由的梁

对于两段直径分别为d1和d2的阶梯轴(图17a))，可以将其看作直径分别为d1和d2的两个两端自由的梁耦合而成(图17b))［9］。其组件的频率响应矩阵如式(3)所示(大写字母表示组件的位移、转角、力、力矩及频响函数，小写字母表示对应的部件)。

图17 阶梯轴组件和部件的示意

阶梯轴左端面处的频响函数G11为

同理，将过盈配合看作轴和轴套的柔性耦合，见图18。在其结合面上选择两端点及中点为耦合点，在耦合点处建立弹簧阻尼单元来表示结合面的接触刚度和接触阻尼。同样，大写字母表示组件的位移、转角、力、力矩及频响函数，小写字母表示对应的部件。

图18 过盈配合理论模型

耦合点处的弹簧阻尼单元表示为刚度矩阵:

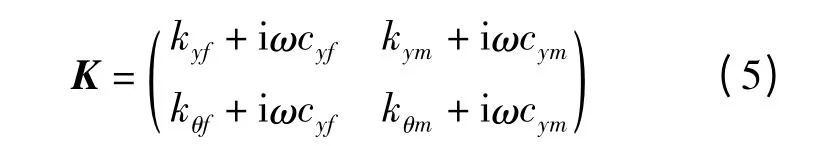
式中:kyf，kym，kθf，kθm，cyf，cym——有限元计算得到的过盈配合结合面接触刚度和接触阻尼。

过盈配合组件左端面处的频响函数G11为

式中:q1/Q1为A的前两列构成的矩阵，q2/Q1为A的3、4列构成的矩阵，q3/Q1为A的5、6列构成的矩阵。

在实际中，常常得到是加速度对力的频响函数，这里可以用式(8)将H11(力对位移的频响函数Y/F)换算为加速度为单位的频响函数H11a。

3.2 频响函数计算及对比

将图1所示研究对象等效为理论模型，见图19。理论模型分为I、II两个部分:I为一个细长轴;II为等长度的同心轴和轴套在两端及中点处耦合(z=0，50，100 mm处)，耦合点的刚度矩阵分别为K1、K2、K3，由有限元仿真计算获得;I、II两部分采用刚性耦合。以配合U7/h6为例，其刚度矩阵取值见表2(其中阻尼值为各载荷下的平均值)。

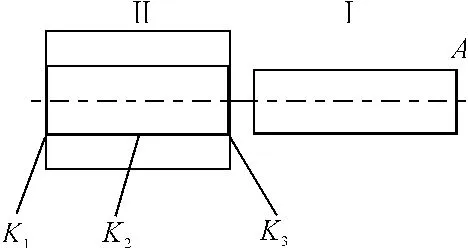
图19 过盈配合组件理论模型

过盈配合组件的频率响应函数测试系统，见图20。将组件用弹簧吊起，模拟自由状态，力锤采用Endevco公司的Modal hammer 2302-10，数据采集卡为NI 9234，测试分析软件采用Modal-VIEW。在过盈配合组件右端安装加速度传感器，测量竖直方向的加速度。使用力锤竖直敲击过盈配合右端。采集力锤的冲击信号及加速度响应信号，输入计算机计算得到过盈配合右端点的原点频响函数。实验中，锤击取3次平均，采样率为25 600 Hz，采样时间为1 s。

表2 U7/h6刚度矩阵参数

图20 过盈配合组件频响函数测试示意

对于配合U7/h6，根据结构响应耦合方法，计算图19中A端面处的原点频响函数。计算值和测试值的对比见图21，图中实线为理论计算结果，虚线为表面实测值。可以看出实验值和计算值比较吻合，各阶固有频率误差很小，见表3，从而证明了有限元计算获得的接触刚度和接触阻尼的正确性。

由表3可见，在不同过盈量下，固有频率的计算值与实验值均差别很小，从而证明通过有限元计算获得的结合面参数的正确性。同时，可以总结出过盈量的变化对结构的固有频率影响很小。

图21 配合U7/h6端点A处原点频响函数

表3 固有频率计算值与实验值对比

4 结论

本文研究了运用有限元法计算过盈配合结合面的接触刚度和接触阻尼，得到了在不同过盈量下，接触刚度和接触阻尼沿轴线方向的变化规律。最后，结合实验测试和结构响应耦合计算，验证了接触刚度和接触阻尼的有效性。根据计算得到的接触刚度和接触阻尼，可以得出:不同的过盈量对接触刚度和接触阻尼的影响较小。因为过盈配合中，轴和轴套已经紧密结合，过盈量的变化，对结合面特性，乃至整个结构的特性影响很小。

［1］韦念龙，邓 群，周 晔，等.有限元分析软件在过盈配合联接安全核算中的应用［J］.安全与环境工程，2002，9(3):37-40.

［2］陈 连.基于可靠性优化技术的计算和选择过盈配合的新方法［J］.机械强度，2003，25(5):519-522.

［3］SCHMITZT，POWELL K.Shrink fit tool holder connection stiffness/damping modeling for frequency response prediction in milling［J］.International Journal of Machine Tools＆Manufacture，2007(47):1368-1380.

［4］张洪武，廖爱华，吴昌华.压气机过盈配合的弹塑性有摩擦接触的研究［J］.工程力学，2007，24(1):186-192.

［5］郭爱贵，范为民，孙 伟，等.基于有限元法的过盈配合接触特性分析［J］.成组技术与生产现代化，2009，26(4):4-7.

［6］赵 玫，周海亭.机械振动与噪声学［M］.北京:科学出版社，2008.

［7］PARK S，ALTINTAS Y，MOVAHHEDY M.Receptance coupling for end mills［J］.International Journal of Machine Tools and Manufacture，2003，44(11):1151-1161.

［8］BISHOPR E D，JOHNSON D C.The mechanics of vibration［M］.Cambridge:Cambridge University Press，1960.

［9］SCHMITZ T，DUNCAN G S.Receptance coupling for dynamics prediction of assemblies with coincident neutral axes［J］.Journal of Sound and Vibration，2006，289(4-5):1045-1065.