城市复杂道路网络交通流的分解模型*
2013-06-08温凯歌
温凯歌,张 菁
(长安大学电子与控制工程学院,陕西 西安 710064)
1 引言
交通模型是描述交通流状态的时空变化、分布规律及交通控制变量之间关系的方程式或映射,是进行交通管理的基础工具。目前的研究中,往往将城市区域交通模型[12]和城市快速公路模型[3]分别对待,可以融合城市公路和快速公路的模型较少。本文在现有交通流宏观模型的基础上,提出了改进的模型,并进行了相应的理论分析。将城市的复杂道路网络进行分解,提出了包含交叉口动态子模型和单向环形道路子模型的复杂网络分解模型。并在最后使用实测数据对模型的有效性进行了验证。
2 复杂道路网络的分解
交叉口最常用的是排队消散模型[4],于1982年由Hunt等人提出,它描述了单独的信号交叉口交通流行进过程,并建立了相应的约束条件。该模型已经被广泛用于世界各地的大城市交通管理系统中[5]。本文在此基础上,提出了新的交叉口模型。
目前,国内外学者提出了多种形式的高速公路及城市交通流模型[6~8],其中应用最广泛的就是希腊学者Papageorgiou 于1989 年提出的宏观模型[6]。本文对该模型作了进一步改进,提出了基于OD 的环形道路模型。目前我国城市道路主要街道上,都实行机动车与非机动车分道行驶,如果只考察机动车道,而将道路中部的少部分驶入车辆模拟成为匝道驶入,那么高速公路模型对于城市道路也是适用的。
本文将复杂的城市道路网络进行分解。城市是由一个个的街区组成的,街区之间由街道隔离开,街道交汇的部位便形成交叉口,如图1所示的是西安市部分街道组成的简单网络。我国的交通规则是靠右行驶,那么对于任何一个街区,包围它的街道的内侧部分都可以看成是顺时针的单向环形道路。交叉口可以看成是一个具有输入和输出的黑箱。

Figure 1 Urban traffic network图1 典型的城市交通网络
通过这样的划分设定后,任何复杂的道路网络都可以分解成为单向环形道路加节点的形式。
3 平面交叉口模型
相邻几个街区的结合部就形成了交叉口,我们这里对交叉口进行新的划分,对交叉口周围的街区进行编号,如图2所示。图2是一个十字交叉口,在它的四周有四个街区,使用虚线将其划分为四个部分。
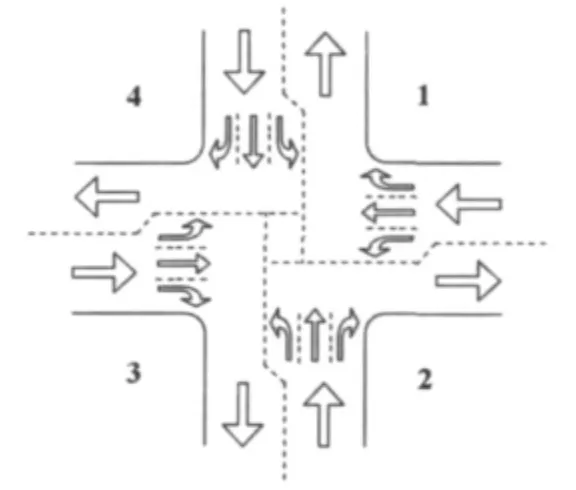
Figure 2 Urban intersection图2 典型的城市交叉口
规定在交叉口处,右转、直行和左转都有各自的专用车道,并且直行和左转车辆不得占用右转车道,那么可以认为在右转车道上车流处于畅行状态,紧贴于一个街区的两条路段可以看成是一条连续的路段,而在交叉口处包含了一个出口和一个入口,如图3所示。例如图2中的1部分可以转化为图3描绘的情形。
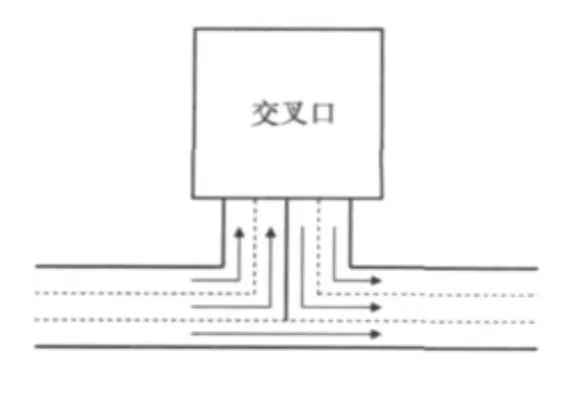
Figure 3 Deformation of partial intersection图3 交叉口一部分的变形图
经过上面的划分变形之后,十字交叉口就会演变成如图4所示的图形。同样,多支路的交叉口都可以变换为这样的形式,如图4所示。

Figure 4 Deformation of whole intersection图4 交叉口整体的变形图
下面以图4所示的典型十字交叉口为例,详细描述交叉口的交通流演化和行进过程。给出一个新的交叉口模型。对四个区域进行编号,从1 到4。那么,各个流向上车辆的排队数可以表示为:
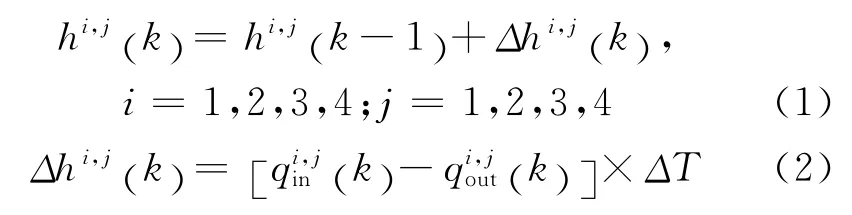
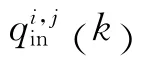
在k时间段,从i方向驶入并前往j 方向的输入流为:
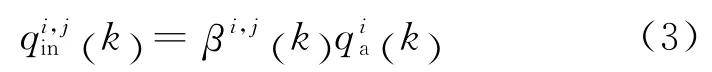

公式(4)说明,各方向车流(左转、直行和右转)的比例之和应该为1。转向比是一个随时间变化的动态值,具有很强的随机性,在实施控制时需要对其进行预测。有很多预测方法可以使用,不再赘述。
在k 时间段各方向减少的排队车辆数由下式确定:

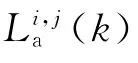
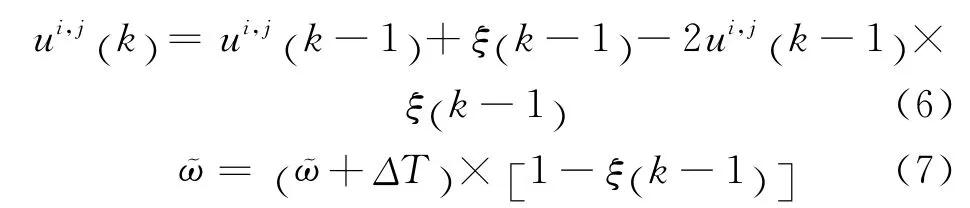
其中,ξ(k)是一个相位切换标志,如果k 时间段结束时,当前相位结束并切换到下一个相位,则ξ(k)=1,否则ξ(k)=0。表示当前相位持续时间长度。相位切换标志ξ(k)可以进一步被表示为五个变量的函数,即上一时段排队长度hi,j(k-1)、该方向当前时段的输入流、当前相位持续时间长度ζ及其上下界(ζmin,ζmax),如下式所示:

综上所述,可以归纳单个交叉口的动态模型为:
交叉口在k时间段的驶入流向量为:

将向量转换成如下矩阵形式:

交叉口在k时间段的车流分流比矩阵为:
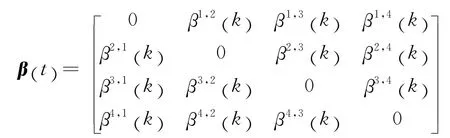
则有各流向的排队输入矩阵为:
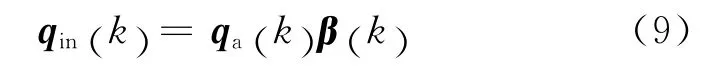
交叉口在k时间段的控制矩阵为:

交叉口在k时间段的车道分配矩阵为:

在k时间段,各流向驶离的车辆数矩阵为:
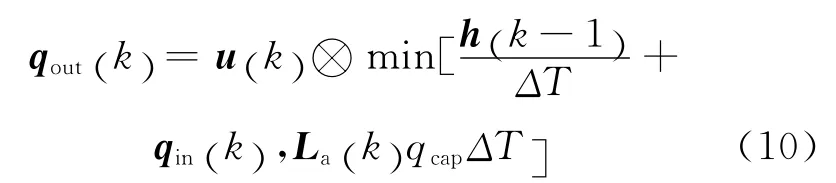

控制矩阵可以表示为:
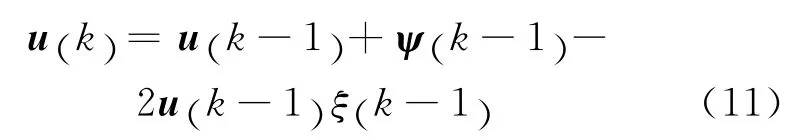
其中,ψ 为相位切换标志矩阵,其元素由下式确定:

交叉口在k时间段的排队矩阵为:

交叉口在k时间段的驶出流向量为:
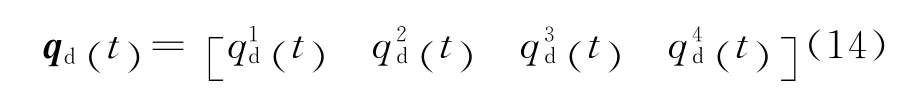
控制器的任务就是在每一个控制周期,确定出相位切换标志ξ(k),从而根据式(12)确定出切换标志矩阵ψ,最后由式(11)得出信号控制矩阵u。
4 单向环形道路模型
METANET[9]是一个宏观交通建模和仿真工具。METANET 有两种表达形式:基于目的地的模型和不基于目的地的模型。如果要考虑到车流的路径诱导,可以使用基于目的地的模型[10]。
本文在METANET 的基础上提出了METANET-OD 模型。在METANET-OD 中,交通网络被定义成包含路段和节点的有向图,并且包含起讫点。图中的节点被设置在公路的分叉点或汇合点处,以及入口匝道和出口匝道。
设单向环形道路总长度为L,将其划分为N个等长度的片断,ΔL=L/N。其中包含了O 个入口匝道和D 个出口匝道,如图5所示。

Figure 5 One way ring road图5 单向环形道路简化图

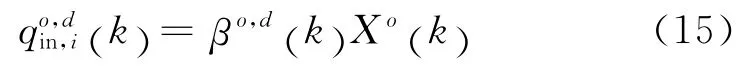
其中,βo,d(k)表示OD 矩阵中从入口o出发到达出口d 的车流占总的出发车流的比例,Xo(k)表示从入口o 出发的交通需求。那么,部分交通流密度通过下式进行更新:



边界情况,当i=1时,第一个路段的上游就是第N 个路段:
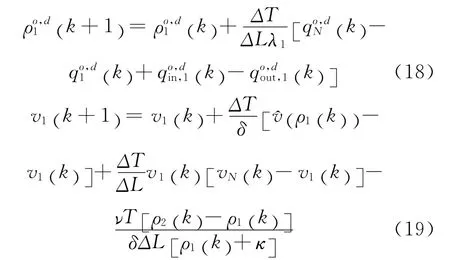
上式中,未指明参数含义与文献[9]中相同。
当i=N 时,第N 个路段的下游就是第1个路段,平均速度为:

路段i上,从入口o出发到达出口d 的部分交通量为:

其中,α为模型调整参数,正常情况下为1。路段i上总的交通流量为:

在k时间段,从出口匝道d离开的车流总量为:
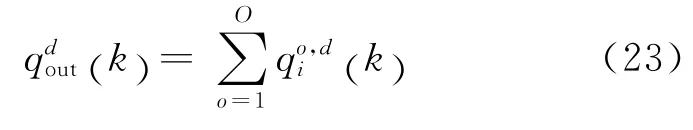
5 仿真实例
为了验证本文所提模型的准确性,对西安市某局部路网构成的交通网络进行了仿真,如图1 所示。采用实测数据与仿真结果进行对比,实测数据来自于2008年6月12日早7:00~10:00,总共3个小时,采样周期为1分钟,总共180个时间段。
首先使用上面提出的方法对网络进行分解。我们考虑到在每一个街道内部都会有交通流的产生和消灭,那么就假设在每条街道的中部存在一个出口和一个入口。对于图中四个角上的部分,右转车流并不进入我们所考虑的网络中,将其省略,因此,在每个角上,交叉口都有一对直接的出入口。分解后的效果如图6所示。
分解后,网络包含:四个典型交叉口,一个具有8对出入口的单向环形道路网,四条具有3对出入口的路段。

Figure 6 Simple network decomposition diagram图6 简单网络分解图
仿真结果如图7所示。由图7可见,仿真结果与实际交通数据很接近,说明该模型结构适当,参数准确,精度较高。模型中提供了控制接口以及区域中各交叉口排队长度、到达车辆数、离开车辆数,为实现各种控制方案提供了方便。

Figure 7 Simulation results of link 1图7 路段1仿真结果
6 结束语
本文提出的动态离散方程可以作为城市大交通网络的控制仿真模型。该模型简捷、易于计算,较好地反映了城市路网的交通流信息。首先,分解模型可以将大型网络进行分解,降低建立模型的复杂性。其次,可以将城市道路和快速公路方便地连接起来,建立大规模交通通道网络。第三,提供了控制接口,使得控制方案方便地应用在网络中。
但是,在现实中,在路段中部交通流的产生与消灭情况非常复杂,影响的因素很多。另一方面,非机动车和行人的因素对于车流的产生和运行也有较大的影响,这两个因素是未来交通网络模型必须考虑的关键。
[1]Lo H K,Chan G E,Chan Y C.Dynamic network traffic control[J].Transportation Research,2001,35A(1):721-744.
[2]Hu Jun-hui,Yang Li,Kong Ling-jiang,et al.Urban mixed traffic flow considering the influence by origin-destination of public transportation[J].Journal of Transportation Systems Engineering and Information Technology,2011,11(1):102-107.(in Chinese)
[3]Zhang Jing,Ju Yong-feng.Research on traffic flow model of expressway weaving area[J].China Journal of Highway and Transport,2011,2.(5):89-93.(in Chinese)
[4]Hunt P B,Robertson D I,Bretherton R D.The SCOOT online traffic signal optimization technique[J].Traffic Engineering &Control,1982,2.(4):190-192.
[5]Wey W M.Simulation-based performance studies of utilizing network programming algorithm to a network-wide traffic control[R].TRB Annual Meeting,Transportation Network Modeling,2004.
[6]Kotsialos A,Papageorgiou M.Coordinated and integrated control of motorway networks via non-linear optimal control[J].Transportation Research Part C,2002,10(1):65-84.
[7]Zhang Meng-meng,Jia Lei.Mathematical model of traffic flow on arteries with coordinated control system[J].Control Theory &Applications,2011,2.(11):1679-1684.(in Chinese)
[8]Guo Hong-wei,Gao Zi-you,Xie Dong-fan.The influence of U-turn movement on the dynamics of traffic flow[J].Acta Phys Sin,2011,60(5):058902-1-10.(in Chinese)
[9]Messmer A,Papageorgiou M.METANET:A macroscopic simulation program for motorway networks[J].Traffic Engineering Control,1990,31(9):466-470.
[10]Kotsialos A,Papageorgiou M.Traffic flow modeling of large-scale motorway networks using the macroscopic modeling tool METANET[J].IEEE Transactions on ITS,2002,3(4):282-292.
附中文参考文献:
[2]胡君辉,阳丽,孔令江,等.考虑公交起迄站点影响的城市混合交通流研究[J].交通运输系统工程与信息,2011,11(1):102-107.
[3]张菁,巨永锋.快速路交织区交通流模型研究[J].中国公路学报,2011,2.(5):89-93.
[7]张萌萌,贾磊.城市协调控制主干路交通流模型[J].控制理论与应用,2011,2.(11):1679-1684.
[8]郭宏伟,高自友,谢东繁.城市道路U 形转向交通流特性模拟分析[J].物理学报,2011,60(5):058902-1-10.
