一种新的高速机动目标跟踪算法的研究
2013-06-08郑庆琳
孟 凡,郑庆琳,倪 雪,刘 建
(1.中国船舶重工集团公司第七二四研究所,南京 210003;2.中国人民解放军理工大学 通信工程学院,南京 210007)
0 引言
机动目标跟踪是雷达数据处理的一个重要课题。目前,随着目标自身的机动特性的不断提高,对机动加速度大范围变动或突变的机动目标的跟踪问题已经受到广泛的关注,跟踪高速机动目标是现代雷达系统必须要解决的问题。
机动目标跟踪的最大难点在于机动目标模型并不能满足实际运动的需要。传统方法往往是针对目标机动模型本身,加入相关的机动变化量或采用多模型的方法,得到目标状态的最佳位置估值。本文从数据关联的角度出发,结合线性回归和聚类分析理论,设计出一种新的高速机动目标跟踪算法。该算法利用机动目标的历史航迹参数建立样本集,依据回归分析设计关联波门,进行航迹分裂,形成多航迹;然后对目标航迹样本集中的样本进行投影,并提取特征向量,计算类内相似度;同样方法也得到分裂航迹参数的投影值,即待分辨样本;最后,根据相似度判别准则提取出属于感兴趣目标的航迹,实现高速机动目标跟踪。该算法相比于传统方法具有计算量小、抗干扰性强等优点,为机动目标的跟踪提供了新的解决方案。
1 算法原理
1.1 关联波门
目标跟踪过程中,由于目标发生机动,常常导致跟踪不稳定致使目标丢失。从数据关联的角度,可以认为是没有找到合适的观测数据与目标航迹关联。如果为了保证跟踪的稳定性,扩大波门,又会导致干扰的增加。
基于以上情况,针对直线机动和转弯机动,本算法设计了两种波门,如图1所示。当目标发生机动时,以上一个周期的滤波点A为圆心,当前外推点B 到A的距离为半径,当前航向为基准分别向左右旋转角度θ,以C 点和D 点为中心分别建立波门,此类波门主要针对机动转弯的情况;作C 点和D 点的切线相交与E点,以E 点为中心建立波门,此类波门主要针对直线机动的情况。
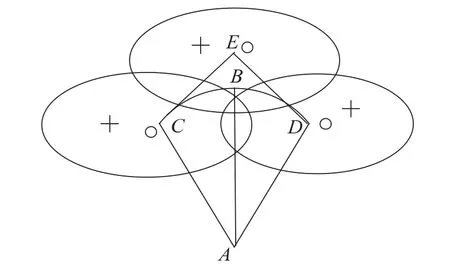
图1 关联波门
发生在两次机动之间的航迹可以被认为是由散列在某一直线附近的点迹所形成的。这些点迹可被看成是每个独立的样本,故可构建每个观测点的滤波坐标值的样本集。

随机变量y与可控变量x 满足:

其中a、b、σ2(σ=1)为常数,则称η与x 之间存在线性相关关系,称式(1)为一元正态线性回归模型,并对模型中的a和b 进行参数估计。

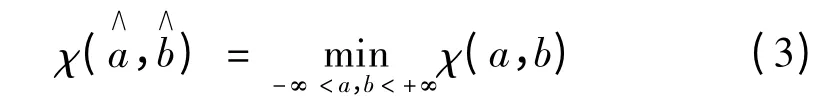

1.2 目标分辨
根据已建立的波门,进行点迹关联(每个波门内只选择最近关联到的点迹),并分别建立备选航迹ψ1,ψ2和ψ3。然后,对航迹参数进行特征提取,并根据模糊聚类原理选择出属于感兴趣目标的航迹。
1.2.1 特征提取
特征提取的基本任务是,在保证分类正确的前提下,通过某种数学变换产生出对分类识别最有效的且具有一定可靠性和独立性的分类特征。该特征往往是由特征向量的一个分量所表示,同一类模式之间的相似性以及不同模式之间的差异性主要体现在这些分量所表示的特征上。
图2为目标在运动过程中形成的轨迹,从0时刻起始(A 点),到i时刻结束。设A 点为投影中心,假如目标在i+1时刻发生机动,那么对i时刻之前的历史点迹依次向A 点投影。首先,按照运动学公式,根据切向速度和法向速度得到相邻周期间的切向和法向的距离差△x和△y;其次根据式(4)和式(5),已知xi和yi,切向和法向的距离差△x和△y,航向角φ,即可推出xi-1和yi-1。
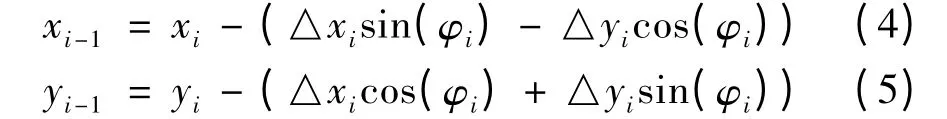
其中φ为当前航向。这样在A 点附近形成了以A 点为中心的样本集,并以这些样本建立特征向量α=[xA1,xA2,…,xAn],同理可得β=[yA1,yA2,…,yAn],其中i为累积量,i=1,2,…,n。
1.2.2 聚类分析
聚类分析就是按照一定的要求和规律对事物进行区分和分类的过程。在这一过程中不需要先验知识,仅靠事物间的相似性作为类属划分的准则。它把没有类别标记的一系列样本按照某种准则划分成一个或若干个子集,使相似的样本尽可能归为一类。

图2 点迹映射
(1)数据标准化


(2)类内相似关系

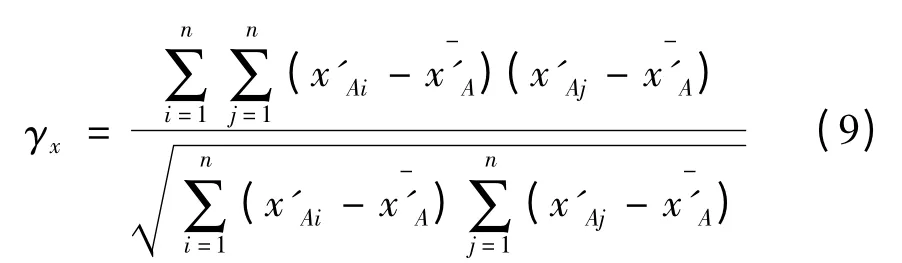
(3)相似性度量
两个特征向量之间的距离是它们相似性的一种度量。根据已经形成的聚类Γx和Γy获取聚类均值点,如式(10)所示。若Ni是第i 聚类Γi中的样本数,mi是这些样本的聚类中心。

根据欧式距离计算样本x与聚类均值间的距离,判别样本是否属于该类。其中,c为聚类个数。
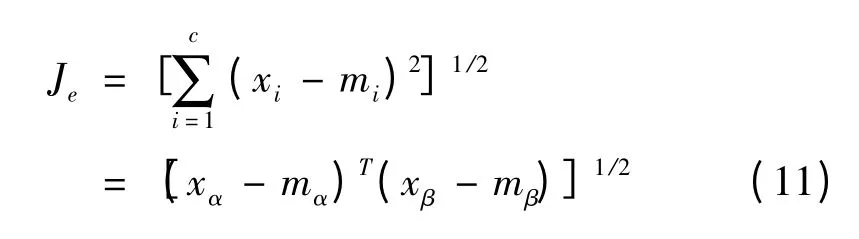
2 算法步骤
(1)由样本集Z,根据式(1)、(2)和(3),得到a和b的参数估计值:
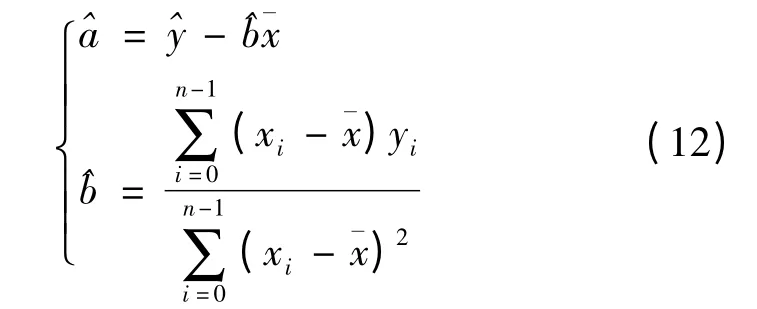
(2)进行点迹关联和两点建航,得到备选航迹ψ1的参数[xψ1,vxψ1,axψ1,yψ1,vyψ1,ayψ1],同理可获得航迹ψ2和ψ3的参数(如果检测到点迹);
(3)针对特征向量α和β,并计算类内相似度γx和γy;
(4)根据式(4)和(5),另航迹ψ1(航迹ψ2和航迹ψ3同理)向A 点投影,得到待分辨样本(xAψ1,yAψ1)(同理还有(xAψ2,yAψ2)和(xAψ3,yAψ3));

其中△xmax和△ymax分别为类内样本间的标准差;
(6)满足步骤(5),即得到属于感兴趣目标的航迹(如果有多个待分辨样本满足条件,采用最近邻法进行区分)。
3 实验结果分析
本算法的滤波模型采用交互多模型(IMM),模拟目标起始点为(-20000,-10000),初始速度为零,加速度为5 m/s2,加速时间为60 s,之后速度保持不变;然后每次发生机动的时间为8 s,机动加速度为60 m/s2。真实航路如图3所示。图4和图5为目标方位和距离的真实值和滤波值之间的误差。图6和图7为x方向和y方向距离的真实值和滤波值之间的误差。
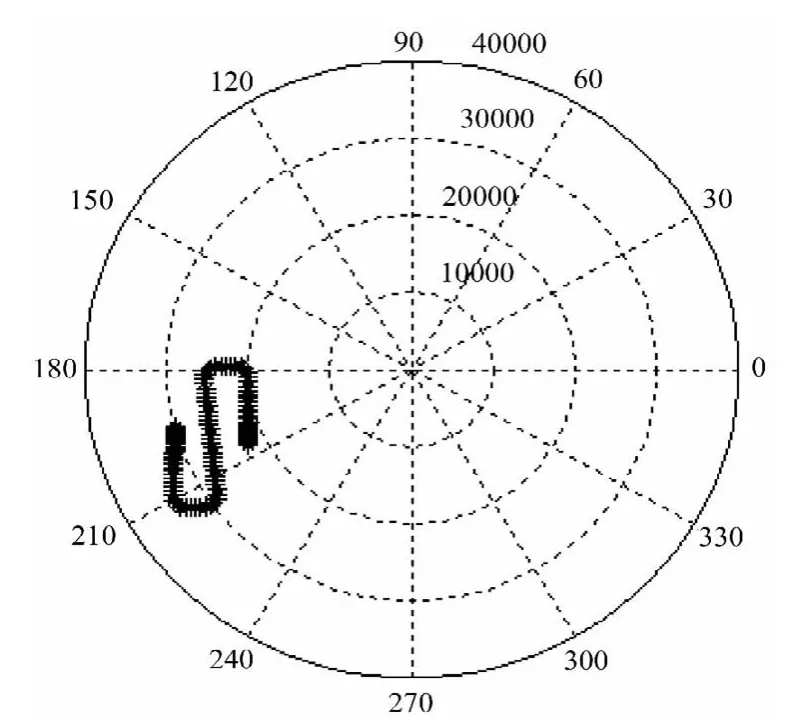
图3 真实航路图

图4 跟踪航路图

图5 方位误差

图6 距离误差

图7 x方向距离误差

图8 y方向距离误差
由图3~8 可以看出,机动致使模型与目标的实际运动失配,产生较大的预测误差,滤波器参数也无法满足跟踪的需要,方位、距离等参数值都有较大的突变。由于采用了本文的方法,在原航迹关联失败后,及时建立波门,进行航迹分裂,并根据提取的特征在关联波门中匹配相关点迹,实现了高速机动目标的稳定跟踪。
4 结束语
本文采用线性回归和聚类分析理论,提出了一种针对高速强机动目标的跟踪算法。该算法能够适应目标的多种机动情况,其中包括直线机动和转弯机动,并可以稳定跟踪目标,其基本思想可以为机动目标跟踪提供新的解决方案,并具有广泛的应用前景。
[1]边肇祺,张学工等.模式识别[M].2 版.北京:清华大学出版社,2000.
[2]周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1994.
[3]A 费利那,F A 斯塔德.雷达数据处理(第一卷)[M].匡永胜,等译.北京:国防工业出版社,1988.
[4]何友,修建娟,等.雷达数据处理及应用[M].北京:电子工业出版社,2006.
[5]Singer R A.Estimation Optimal Tracking Filter Performance for Manned Maneuvering Targets[J].IEEE Trans.on AES,1970,6 (4):473-483.
