基于累积方正弦波插值的抖动信号分选算法

于 岩，张旭洲，李科学

(1.空军航空大学 航空信息对抗系，长春 130022;2.解放军94686 部队，上海 202150)

0 引言

信号去交织一直是信号分选的关键环节，其目的就是提取出交织脉冲串中的每一部雷达脉冲序列。在密集的信号环境中，一般利用脉冲的瞬时参数，即载频(RF）、到达方向(DOA）、脉冲宽度(PW）和脉冲幅度(PA）等，进行预分选，然后再利用脉冲到达时间(TOA）来进行主分选。主分选主要是通过估计各部雷达信号的脉冲重复间隔来完成分选。

目前，信号去交织的方法主要有累积差直方图法(CDIF）［1］、序列差直方图法(SDIF）［2］、基于PRI 变换的方法［3-5］以及基于平面变换［6］的方法。这些方法在处理简单信号时表现出良好的效果，但却无法准确分选出交织脉冲串中的PRI 抖动信号，甚至当简单信号的参数不稳定时分选结果也会十分不准确，因此急需解决PRI 抖动信号的分选问题。

本文提出了一种累积方正弦波插值算法。该算法对脉冲的到达时间差进行累积方正弦波插值，通过快速傅里叶变换从频域完成对抖动信号PRI中心值的估计，再利用脉冲抽取算法完成信号分选。仿真结果表明，该方法能够有效分选出PRI 抖动信号。

1 方正弦波插值基本原理

方正弦波插值算法［7］的主要思想是将离散的到达时间差变换成连续信号，利用傅里叶变换提取出强周期成分后，再利用脉冲序列抽取算法完成信号分选。将傅里叶变换应用于雷达信号分选有以下优点:(1）傅里叶变换能够很好地检测周期信号而不会出现倍频信息，并且傅里叶变换是一种全局变换，不会因为个别点的畸变而改变估计参数的精度，因此方正弦波插值算法能够很好地抗虚警数据和数据丢失;(2）傅里叶变换拥有各种成熟的快速算法，能够保证信号分选的快速完成。

1.1 方正弦波插值函数

雷达信号的到达时间序列就是脉冲前沿的到达时刻:

式中表示一共有N个脉冲，第i个脉冲到达的时刻是ti时刻，T 序列是递增序列，一般可设t1=0。T 序列中相邻脉冲的到达时间差为

因此，给出如下函数:

通过简单的计算可知:

通过式(4）完成了从函数s(t）到T的线性映射，因此就可以研究函数s(t）的特性来研究到达时间序列T的特性。然而，这样变换得到的s(t）特性并不理想，主要表现在其不连续不光滑，而且存在直流分量，这样就给信号的离散化和频谱分析带来了严重的问题。

为了构建利于离散化和频谱分析的光滑连续且没有直流分量的映射函数，提出利用正弦函数代替冲激函数进行插值变换。函数定义如下:

由于函数si(t）的幅度和周期的量值相等，故称其为方正弦波，得到的函数s(t）称为方正弦波插值函数，简称为插值函数。插值函数s(t）和到达时间序列T的映射关系为

插值函数s(t）具有如下性质:(1）连续;(2）一阶导函数连续(光滑）和积分为零(没有直流分量）。证明如下:

由于在ti＜t≤ti+1，i=1，2，…，N－1中s(t）显然是连续和光滑的，所以下面只证明在 T={t1，t2，…，ti，…，tN}，i=1，2，…，N 序列中的时刻点是连续和光滑的。以ti时刻为例:

上述3个公式分别证明了函数s(t）连续性、光滑性和零直流分量。正是由于方正弦函数s(t）有这种特性，才保证了在频谱分析过程中的倍频压制特性和没有杂波分量的优良特性。

1.2 插值函数的谱特征

通过方正弦波插值后，离散的到达时间转化为连续的插值函数。下面分析PRI 固定信号的和PRI 抖动信号插值函数的频谱特征。

(1）PRI 固定信号

PRI 固定调制信号的方正弦波函数为

所以，PRI 固定信号的插值函数为

可见，PRI 固定信号经过方正弦波插值之后是频率为1/△t的单一正弦信号，故其只有在1/△t处出现频线，因此极易检测。

(2）PRI 抖动信号

PRI 抖动信号的PRI 值在一个区间内随机变化。可用如下模型定义抖动序列的PRI:

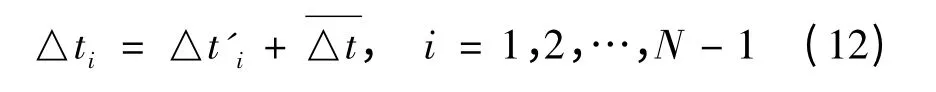
其中

则信号的PRI 抖动量一般可定义为

其值一般不会超过10%。由此可得PRI 抖动信号的方正弦波插值函数为

当抖动信号的抖动量小于10%，式(14）可进一步近似为

所以，PRI 抖动信号的方正弦波插值函数为

从式(16）可以看出，在PRI 抖动调制下方正弦波函数是幅度和相位都受抖动序列调制的函数。当抖动量小于10%时，反映在频域上就是函数在频谱上会略有展宽，谱峰幅度比PRI 固定调制有所下降，谱峰位置出现在1/△t处。

为了更加直观地体现出到达时间序列经方正弦波插值后的频谱特性，本文将PRI 固定信号和PRI 抖动信号插值函数的频谱图绘制出来。图1 是PRI 固定调制信号的方正弦波函数谱图，PRI=1000 μs;图2 是PRI 抖动信号的方正弦波函数谱图，其中PRI中心值为1000 μs，抖动量δ=10%，抖动序列为均匀分布的随机抖动序列。

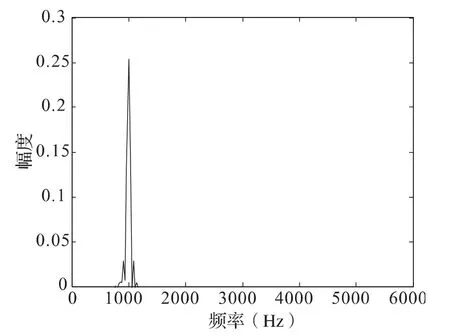
图1 固定信号插值函数频谱图

图2 抖动信号插值函数频谱图

从图1和图2 可以看出，方正弦波插值算法对PRI 固定信号和PRI 抖动信号有较强的适应性和较高的参数估计精度。但是，上述只是对单一雷达信号进行方正弦波插值变换，如对交叠脉冲信号直接进行方正弦波插值变换则不能很好地估计出信号的重复频率。因此，本文将直方图算法中的累积思想应用于方正弦波插值算法，提出一种累积方正弦波插值算法。该算法对交叠信号的到达时间进行累积方正弦波插值，能够很好地估计出雷达信号的重复频率，进而完成对交叠信号的去交错处理。

2 累积方正弦波插值算法

结合式(5）和式(6）可以得出，方正弦波插值的实质是将相邻脉冲的到达时间差进行插值，即将相邻脉冲的到达时间差△t 转化为一个周期为△t的正弦波。因此，方正弦波插值本质上也是对到达时间差进行统计，只是与传统CDIF、SDIF和PRI 变换不同。方正弦波插值算法不逐个统计每个间隔的个数，而是通过对正弦波插值后的函数进行傅里叶变换来提取准PRI，极大提高了算法的抗干扰性能和运算效率。

对于交叠的脉冲信号，本文提出基于累积方正弦波插值的脉冲重复频率估计方法。对应累积直方图算法，一级到达时间差的方正弦波插值称为一级插值函数，前两级到达时间差的累积方正弦波插值称为二级插值函数，三级四级以此类推。

累积方正弦波插值算法首先计算交叠脉冲序列的一级插值函数，以其频谱最大值作为重复频率对原始信号进行脉冲抽取，如果成功抽取序列，则将序列从原始序列中去除;如果抽取不成功，则计算下一级插值函数并与前一级插值函数进行累积，继续检测插值函数的频谱，并进行序列抽取，直至计算至最大累积级数或所剩脉冲数不足以形成一部雷达序列。累积方正弦波插值算法的流程如图3所示。

图3 累积方正弦波插值算法流程图

算法的具体步骤如下:

(1）输入n个雷达脉冲的到达时间，最大累积级数Cthreshold，并令累积级数C=1;

(2）若C=Cthreshold，则算法结束;否则，计算前C级的累积脉冲到达时间差，并将时间差从小到大排序，对排序后的前C 级累积时间差进行方正弦波插值变换，得到方正弦插值函数;

(3）对插值函数进行快速傅里叶变换，提取其频谱最大值Fmax;

(4）以Fmax作为脉冲重复频率进行脉冲序列检索，若检索不成功，则令C=C+1，并转至步骤(2）;若序列检索成功，则将其从原始脉冲序列中去除，如果剩余脉冲可以继续分选，则令C=1，并转至步骤(2），否则算法结束，输出分选结果。

由于修正PRI 变换算法需要计算所有两两脉冲的到达时间差，且采用划分小箱的方式提取PRI，因此，算法计算量非常大。而累积方正弦波插值分选算法不但从一级插值函数开始逐级搜索，而且在脉冲重复频率的提取部分采用具有快速算法的傅里叶变换，极大地增加了分选过程的实时性。

3 仿真实验分析

由于主要将累积方正弦波插值算法应用于PRI 抖动信号的分选，因此本文主要就PRI 固定信号和PRI抖动信号对该算法进行适用性分析。

(1）脉冲总数1500个，包括1 部PRI 固定调制的雷达的脉冲信号，PRI=1000 μs;两部PRI 抖动雷达的信号，其中一部雷达的PRI中心值为730 μs，抖动量δ=3%，另一部雷达的PRI中心值为815 μs，抖动量δ=5%。最大累积级数Cthreshold=5，仿真结果如表1所示。

(2）脉冲总数1500个，包括3 部PRI 抖动调制的雷达的脉冲信号，其中第1 部雷达的PRI中心值为730 μs，抖动量δ=3%;第2 部雷达的PRI中心值为815 μs，抖动量δ=5%;第3 部雷达的PRI中心值为1126 μs，抖动量δ=10%。最大累积级数Cthreshold=5，仿真结果如表2所示。

(3）为了验证累积方正弦波插值算法的实时性，本文以表2的雷达数据为基础，分别采用修正PRI 变换法和累积方正弦波插值算法进行仿真实验。每次仿真实验中每部雷达信号的个数按比例增加，统计每次实验的时间消耗。仿真实验结果如图4所示。

仿真结果表明，本文提出的累积方正弦波插值算法能够有效分选PRI 抖动信号，且无须预先设置容差参数，有效避免了修正PRI 变换中的容差参数设置问题，脉冲的平均分选准确率可达到90%，且通过与修正PRI算法进行时间对比实验，进一步证实了本文累积方正弦波插值算法的时间消耗远远小于修正PRI 变换算法。

表1 算法仿真结果

表2 算法仿真结果

图4 时间消耗对比图

4 结束语

综上所述，本文提出的累积方正弦波插值算法原理简单，算法运算量小，取得了较好的分选效果，且算法采用工程中应用广泛的快速傅里叶变换代替计算量较大的直方图统计方法，使得算法的工程实现变得可能。

［1］Mardia H K，et al.New techniques for the deinter-leaving of repetitive sequences［J］.IEEE proceedings Pt F，1989，136(4）:149-154.

［2］Milojevic D J，et al.Improved algorithm for the deinterleaving of radar pulses［J］.IEEE proceedings Pt F，1992，139(1）:98-104.

［3］Hassan H E.Deinterleaving of radar pulse in a dense emitter environment［C］// IEEE International Conference on Radar.Hilton Adelaide，South Australia，2003:389-393.

［4］Ray P S.A novel pulse TOA analysis technique for radar identification［J］.IEEE Trans.on Aerospace and Electronic Systems，1998，34 (3）:716-721.

［5］Hassan H E.Joint deinterleaving/recognition of radar pulses［C］//IEEE International Conference on Radar，Hilton Adelaide，South Australia，2003:177-181.

［6］Zhao Renjian，et al.Plane transformation for signal deinterleaving in dense signal environment［J］.Acta Electronica Sinica，1998，26(1）:77-82.

［7］Jiang Qinbo，Ma Hongguang，Yang Lifeng.Estimation of Pulse Repetition Interval and Deinterleaving Based on the Square Sine Wave Interpolating Algorithm［J］.Journal of Electronics ＆ Information Technology，2007，29(2）:350-354.