基于不确定项观测器的混沌系统变结构控制

陈秀琴,林莉芸

（信阳职业技术学院,河南信阳464000）

基于不确定项观测器的混沌系统变结构控制

陈秀琴,林莉芸

（信阳职业技术学院,河南信阳464000）

基于不确定项观测器方法研究了一类状态不完全可测的不确定混沌系统的变结构控制问题,提出了利用不确定项的观测值来估计真实值、设计控制器的新方法.适当选择观测器增益可使观测误差充分的小,达到良好的控制效果.最后对Chua混沌系统进行数值仿真,结果表明：方法具有收敛性好、抖振小的优点.

不确定混沌系统；不确定项观测器；变结构控制

自1963年Lorenz[1]发现第一个混沌例子以来,混沌问题的研究得到了蓬勃发展,特别在是保密通信、信息科学、生物、物理等领域的应用引起了人们的广泛兴趣[2-4].但这些研究大多是建立在混沌系统精确的数字模型基础之上的.

由于环境干扰、参数摄动、测量噪声、建模误差等因素的存在,对任何一个稍微复杂一点的物理系统,要得到它的精确数学模型都是不可能的,不确定性是控制系统普遍存在的现象.近年来,不确定混沌系统的研究也受到了极大关注,并随之出现了许多混沌同步和混沌控制方法,如自适应控制法[5]、鲁棒控制法[6]及滑模控制法[7-8]等.但这些方法在处理不确定项时,用不确定项范数的上界作为控制器参数设计的依据,用增大控制增益来抵消不确定性对系统的影响,这样的控制器设计势必保守性大,控制效果差.这一点在滑模变结构、混沌同步控制中表现得尤为突出.因此,分析不确定性对系统的影响,寻找不确定性估计的有效算法,是提高控制精度、改善控制系统动态品质的关键问题.

本文针对状态不完全可测的不确定混沌系统,给出了利用观测器方法来估计不确定项的有效算法.该算法可以通过选取合适的观测器增益来达到满意的估计精度,用此估计方法来设计变结构控制器,为有效抑制滑动模态的抖振,改善系统的动态品质提供了一个可行的途径.

1 问题描述

考虑如下不确定混沌系统

2 不确定项观测器设计

由式（8）得

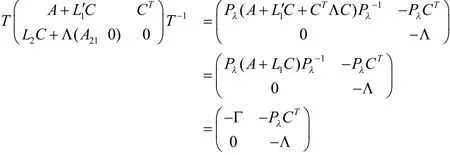
于是误差方程（7）变换为

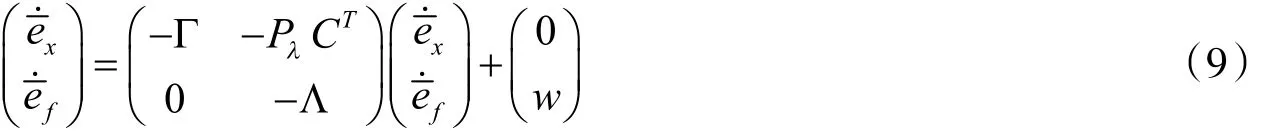
定理1按（4）构造观测器,则有

证明：求解式（9）的第2个子系统方程

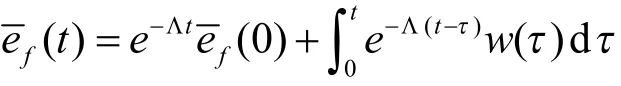
又因为

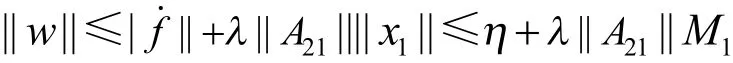
则

求解式（9）的第1个子系统方程

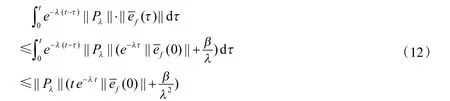
由式（10）

将式（12）代入式（11）得

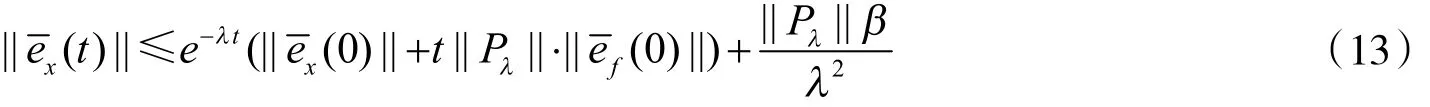
由式（7）、式（10）和式（13）得

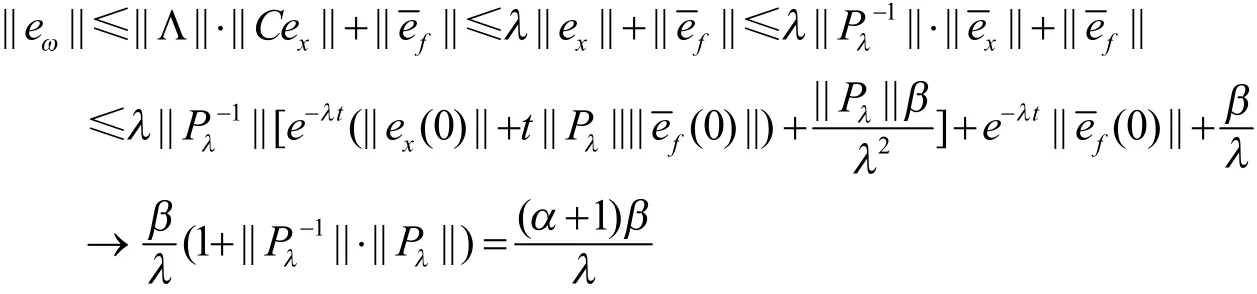
3 不确定混沌系统的变结构控制

定理2取切换函数

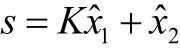
控制律

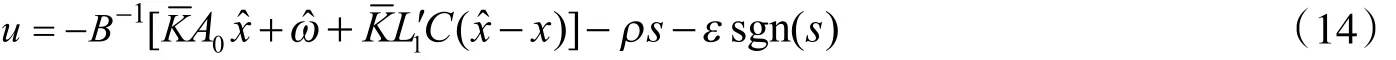
证明：

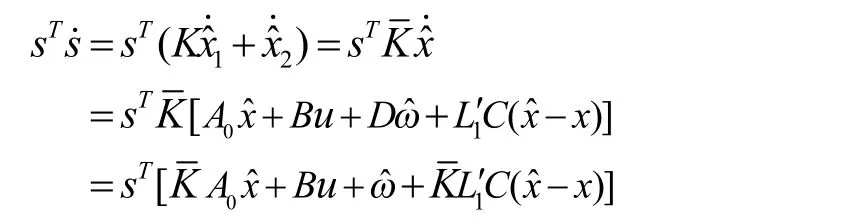
式（14）代入上式得

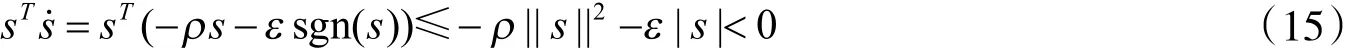
因此,系统（1）任意点出发的运动将在有限时间内到达切换面,并沿切换面渐近到达原点.

4 仿真算例

考虑Chua系统,

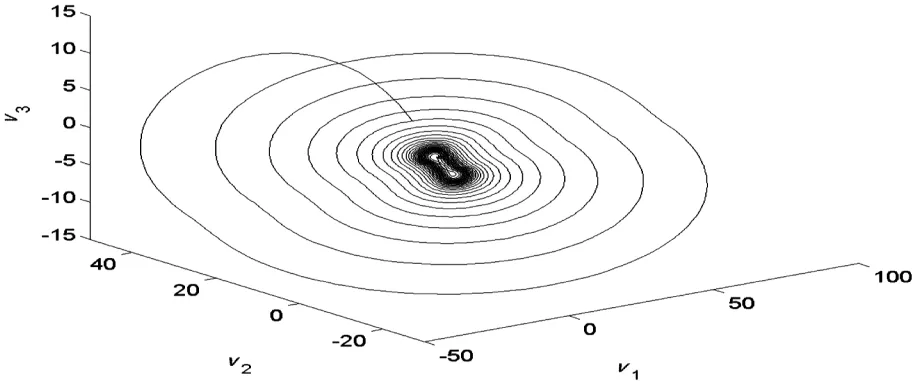
图1 Chua系统相平面Fig.1 Phase planeofChua system’s

利用Matlab软件中Simulink工具箱对以上问题进行仿真,取初始值为（2,1,1）.图2为系统不加控制时的状态轨线,图3为系统在控制律（14）作用下的状态轨线,图4为切换函数的仿真结果.

图2 系统不加控制时的状态曲线Fig.2 State curvewithoutcontrol

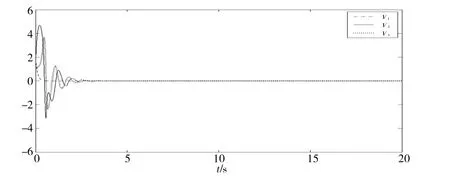
图3 系统在控制律u作用下的状态曲线Fig.3 State curvewith controlu

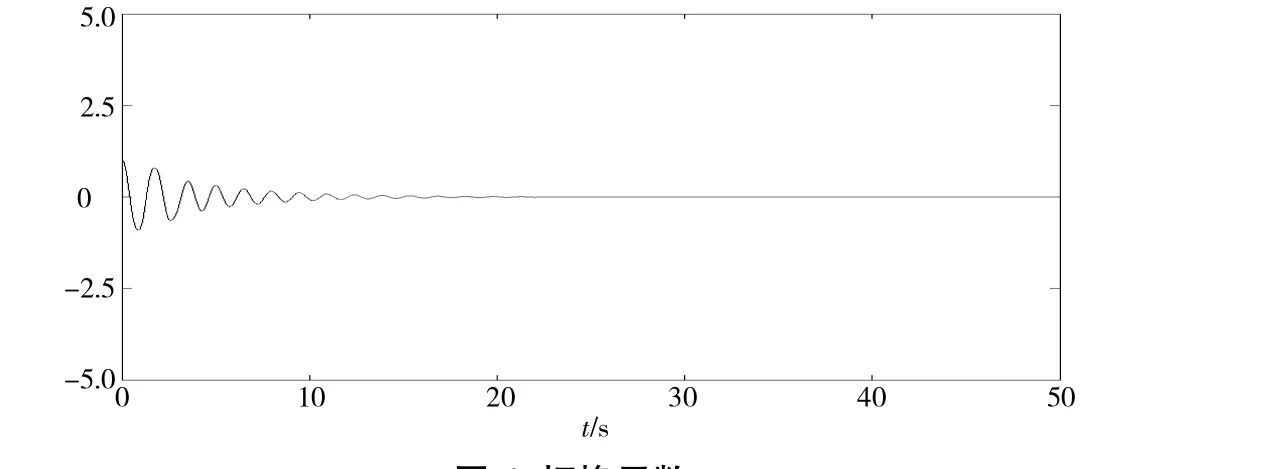
图4 切换函数Fig.4 Switching function

从仿真图像可以看出：按本文方法设计的控制器,有效地减小了抖振,而且收敛性好.

5 小结

针对一类状态不完全可测的不确定混沌系统,提出了一种新的变结构控制方法.该控制器既保证了系统渐近稳定,又很好地改善了系统的动态性能.控制律是基于不确定项的观测值设计的,系统的不确定项得到了有效的补偿,从而有效地减小了抖振,改善了系统的动态性能.

[1]LorenzEN.Deterministic nonperiodic flows[J].Journalof the Atmospheric Sciences,1963,20：130-141.

[2]王元兴,段朝峰.基于线性状态观测器的混沌同步及在保密通信中的应用[J].通信学报,2005,26（6）：105-136.

[3]Boutayeb M,Darouach M.Generalized stated-space observers for chaotic synchronization and secure communication[J].IEEE Transaction on Circuitsand Systems I,2002,49（3）：345-349.

[4]关新平,范正平,陈彩莲,等.混沌控制及其在保密通信中应用[M].北京：国防工业出版社,2002.

[5]Chen SH,Lv JH.Synchronization of an uncertain unified chaotic system via adaptive control[J].Chaos,Solitons and Fractals, 2002,14（4）：643-347.

[6]Yan JJ.Design of robust controllers for uncertain chaotic systemswith nonlinear inputs[J].Chaos,Solitons and Fractals,2004,19（3）：541-547.

[7]Chiang T Y,Huang M L,Yan J J.Slidingmode control for uncertain unified chaotic systems with input nonlinearity[J].Chaos, Solitonsand Fractals,2007,34（2）：437-442.

[8]Zhang Q,Chen SH,Hu YM,et al.Synchronizing the noise-perturbed unified chaotic system by slidingmode control[J].Physica A, 2006,371（2）：317-324.

（责任编辑：卢奇）

Slidingmode control for a class of chaotic system based on uncertainty observer

Chen Xiuqin,Lin Liyun
（Xinyang Vocational&TechnicalCollege,Xinyang464000,China）

The sliding mode control problem of uncertain chaotic system is investigated based on uncertainty observer.A control law using the observer estimation of the disturbance is derived.Moreover the observer can be designed to make the observer error small enough,so we can get satisfying results.Finally,some simulation results about Chua chaotic system are given to demonstrate that the proposed controller has good convergence and little chatting.

uncertain chaotic system；uncertainty observer；slidingmode control

TP13

A

1008-7516（2013）04-0043-05

10.3969/j.issn.1008-7516.2013.04.011

2013-05-14

陈秀琴（1981-）,女,河南信阳人,硕士,讲师.主要从事滑模变结构控制和混沌系统研究.