认知跳频通信抗干扰性能分析

毛留俊，郭建新，姚 昆，王叶群

(空军工程大学信息与导航学院，陕西 西安 710077)

在电磁频谱对抗中，跳频通信因其具有良好的抗远近效应、抗干扰和多址通信能力而备受关注，广泛应用于短波、超短波、数据链通信和卫星通信[1]中。但是随着电磁环境的日益复杂，常规跳频(Frequency Hopping，FH)面临越来越多的挑战。一是常规FH系统存在“盲目”跳频的弊端，为了保持收发两端固定跳频图案的同步，仍然用那些被干扰的信道传输信息，产生了较多的误码，影响了通信质量。二是由于日益复杂的电磁环境，常规FH通信在组网通信时跳频点“碰撞”概率增高，制约了跳频通信网容量的跃升。针对这些不足，J.Zander提出了自适应跳频技术，其原理是在接收端增加了一个实时信道质量评估单元(Link Quality Analysis，LQA)，并通过反馈信道告知发送端，替换误码率较高的信道，但自适应跳频实时性较差，尤其在时变信道情况下抗干扰性能不佳，而且如果干扰频率较多，稳定持续时间太长[2]。1995年，美国Sanders公司发布的相关跳频增强型扩频电台——CHESS(Correlated Hopping Enhanced Spread Spectrum)电台，从高速差分跳频通信新体制出发，大大提高了数据传输率并解决了常规跳频系统抗跟踪干扰和抗多径衰落等问题，但是它组网通信时的多址干扰一直是难以解决的问题[3]。

认知无线电(Cognitive Radio，CR)技术的出现，为解决跳频通信的上述问题提供了新的思路，人们尝试将CR的有关思想融入到FH通信中，提出了认知跳频(Cognitive Frequency Hopping，CFH)技术，其基本思想是将认知无线电的动态频谱接入与跳频抗干扰技术结合，通过感知周围电磁环境，动态遴选出若干个干扰噪声较低的“频谱空洞”作为跳频信号的传输频带，然后在这些频带中进行跳频图案设计，从而在复杂电磁环境中实现有效的抗干扰通信。

Stefa Geirhofer，Lang Tong[4]和美军研究实验室合作，在ISM频段研究WLAN系统的共存问题，采用基于干扰预测的认知跳频方案，开发了试验系统，在机会频谱建模、认知跳频协议建立等方面取得了一定的研究成果。Rongxin Zhi等[5]研究了ISM波段不同设备间的共存，仿真对比了认知跳频技术与自适应跳频技术在蓝牙和IEEE 802.11b设备共存时平均误码率。Philip J.和Colin Brown等[6]讨论了认知跳频技术在225～400 MHz频段的使用问题，提出了多频段调制方案，并对系统在多音干扰下的性能进行了仿真验证。由于他们的研究侧重于设备间的共存以及对各种具体干扰样式的抗干扰性能的深入研究较少，该文正是基于认知FH通信这一新的通信体制在不同干扰样式下的抗干扰性能做出较为具体的理论分析和仿真验证，从而为跳频通信的抗干扰通信研究提供一定的理论依据。

1 认知FH通信系统结构

在分析研究认知FH实现功能的基础之上，本文提出一种认知FH通信系统的实现方案，其基本结构组成如图1所示，主要由跳频单元和认知单元组成。认知FH系统与常规FH的不同之处在于其跳频图案不像常规FH那样事先规划好[7]，在整个通信中几乎不变，而是在认知单元中频谱检测模块的控制下来动态变化和更新的，这种不同正是为了保证信息在更好的信道上传输而存在的。而本文设计的系统与以往的认知FH系统的最大创新就是设置了发送频率集和接收频率集两种频率工作表，并且均是实时动态变化的，主要目的是为了系统最大化地利用现有的频谱资源和实现最可靠的信息传输。

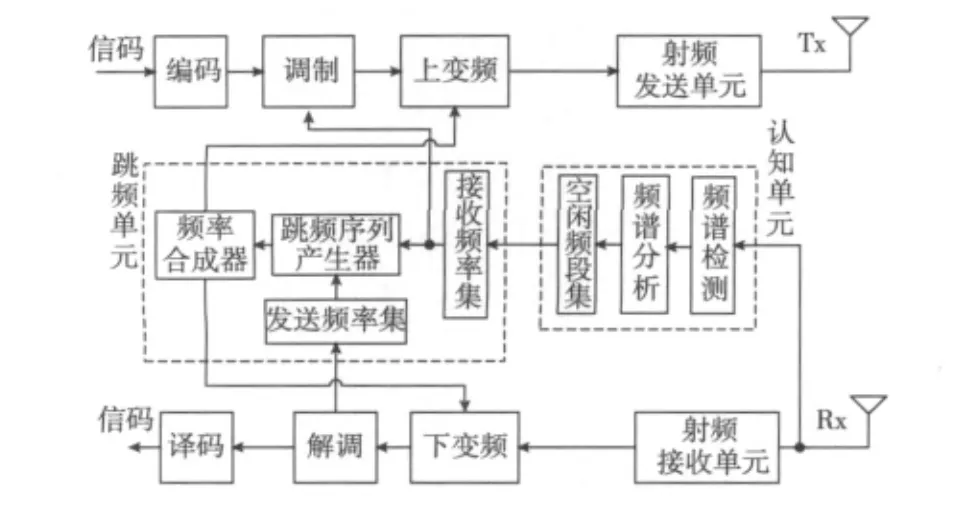
图1 认知FH通信系统结构

从图1可以看出，在发送端，待传信息经过编码之后进行调制，再与频率合成器输出的载波频率进行上变频处理，经发送单元发送出去。在接收端，一方面，认知单元获取来自接收单元的射频信号，通过检测和相应处理，认知单元给出整个工作频段内的频谱感知结果，按照一定准则遴选出若干个干扰噪声相对较低的“频谱窗”，并在这些频谱窗中进行跳频信道选取和跳频图案生成。根据跳频图案信息，跳频序列产生器产生相应的跳频序列，控制频率合成器产生对应的载波信号，为下一时段跳频发送做准备。另一方面，接收端对当前的有用信号进行接收，由于接收信号载波频率是跳变的，因此要求本地频率合成器在同步电路的支持下与之同步，然后解调、译码，恢复出对方的发送信息。本文对认知FH各模块的工作原理不做详细介绍，侧重对认知FH的抗干扰性能进行分析与验证。

2 抗干扰性能分析

本文就认知FH与常规FH在单频、多频和部分频带干扰等常见的干扰形式下的抗干扰性能进行分析。为简单起见，假设两个系统已实现理想同步，传输的信息数据比特流未经任何信道编码和交织;信道为高斯白噪声信道，所有的信道可用，且等概率使用。

1)单频干扰

单频干扰是在跳频系统工作频带内的某个信道上，用大功率干扰机连续发射信号进行干扰，可以用落于跳频系统频带内某一信道的单频正弦波作为仿真模型。

文献[8]指出，在高斯白噪声信道中，对于采用BFSK调制的常规FH系统，接收端采取非相干解调，且不存在外界干扰时的误比特率为

高校机关工作人员作风建设的难点在于长效和常态，很多高校在进行机关工作人员作风建设时，存在阶段性、短期性、突击性的特点，管理严格、监管力度大则作风情况好，反之则出现工作懈怠、效率低下的情况。要实现常态化的工作作风管理和建设，可以尝试从以下几个方面着手，重点突出理念内化、以技术管人、以制度管人的思想。

式中:Eb为每比特的信号能量;N0为高斯白噪声功率谱密度。

在单频干扰下，常规FH的平均误比特率为

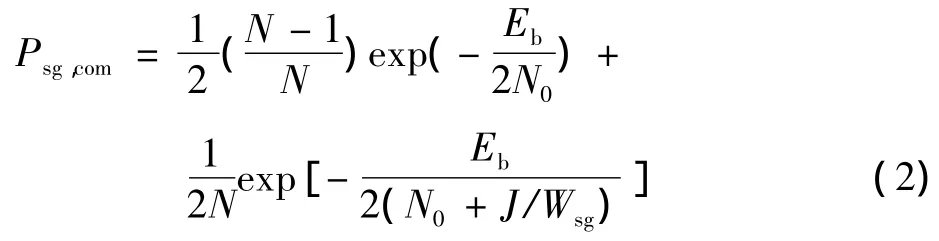
式中:N为跳频的工作信道总数;J为单频干扰的干扰功率;Wsg为单频干扰的带宽。

在认知FH系统中，认知单元实时检测到单频干扰存在，避开该干扰频点，选择其他无干扰的跳频点生成跳频图案进行通信。因此，认知FH系统的误比特率就等同于在高斯白噪声情况下的误比特率，其表达式与式(1)相同。

2)多频干扰

多频干扰是在跳频系统工作频带内的多个频点上，用大功率干扰机连续发射信号进行干扰，可以用多个频率点落于跳频系统频带内的正弦波作为仿真模型。假设常规FH系统和认知FH系统在njam个离散的信道同时被多个连续波干扰，且每个信道的干扰功率相同。

在多频干扰下，常规FH的平均误比特率为

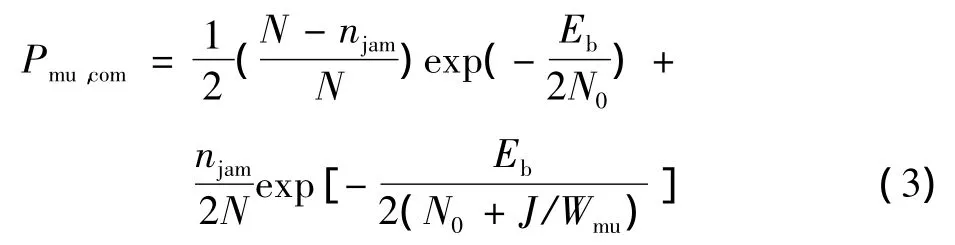
式中:N为跳频的工作信道总数;njam为多频干扰占用的跳频信道数;J为多频干扰的干扰功率;Wmu为多频干扰的带宽。

3)部分频带干扰

部分频带干扰是在跳频系统工作频带内的连续多个相邻信道上，用大功率干扰机连续发射信号进行干扰，可以用一个零均值的宽平稳高斯过程作为仿真模型。根据是否存在干扰，可以将系统的工作带宽划分为受干扰的频带和未受干扰的频带。假设系统的工作跳频信道数为N，其中受部分频带干扰的跳频信道数为m，假定部分频带干扰的干扰功率J均匀分布在这m个跳频信道上。定义干扰因子，干扰功率谱密度，则。下面分别对常规FH和认知FH的抗部分频带干扰性能进行分析。

由于常规FH不能有效甄别出哪些信道已经被干扰，所以仍然会在这m个被干扰的信道上传输信息。在常规FH中，被干扰信道处的误码率为，而在未受干扰信道处的误码率为，因此，常规FH系统的平均误码率为

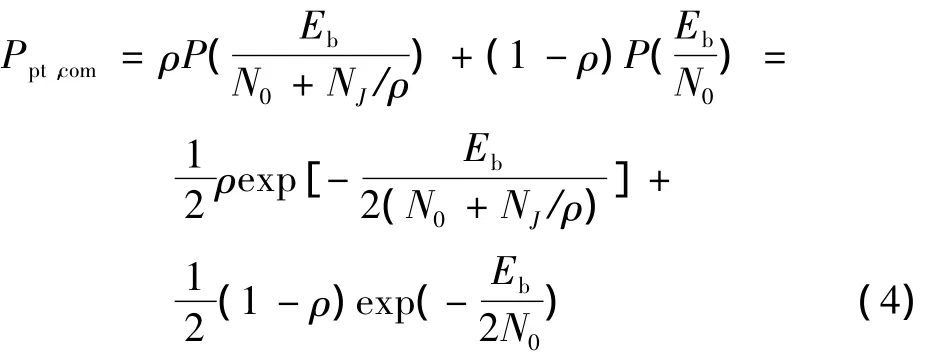
在认知FH中，系统利用频谱检测模块找出干扰频段，避开选择位于干扰频段中的信道作为工作信道，而选择无干扰或者干扰较低的信道生成跳频图案进行通信，从而有效地降低了误码率。假设t时刻从N个跳频信道中选取Na(Namin≤Na＜N，Namin为认知FH正常工作时所需的最小信道数)个信道作为跳频信道，然后以这些选出的信道生成跳频图案进行伪随机跳变。

为简单起见，假定在干扰因子ρ的作用下，未被干扰的信道数能够始终满足认知FH正常工作时所需的最小信道数，即N－m≥Namin，认知FH肯定能避开全部m个干扰信道，因此，其误比特率的表达式与式(1)相同。

3 性能仿真分析

仿真参数:系统采取FSK调制，跳频信道数N=80，信道带宽为1 MHz，跳速为1600 hop/s(跳/s)，信息速率为1600 bit/s，常规FH系统工作信道数为N=80，其工作带宽为80 MHz。认知FH的工作信道数的最小值为Namin=40。

1)抗单频干扰性能

假设常规FH和认知FH在第60个信道f60=60 MHz上都受到单频干扰，认知FH与常规FH在不同信干比下误比特率随信噪比SNR变化的曲线如图2所示。

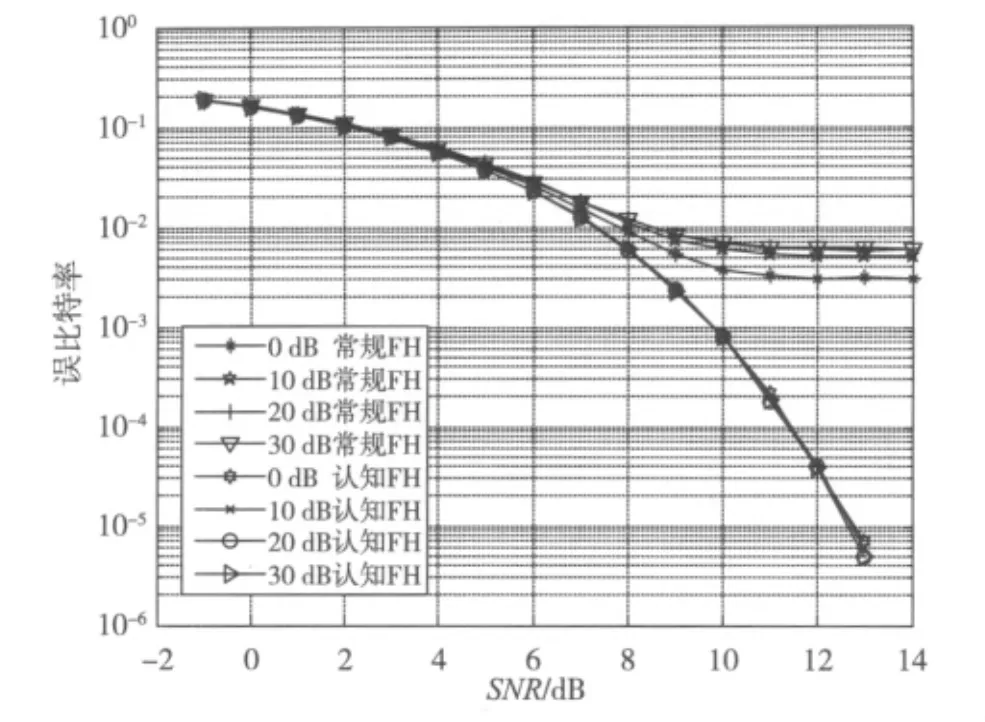
图2 单频干扰下认知FH与常规FH的误比特率曲线

从图2可以看出，从SNR=6 dB之后，认知FH较常规FH具有更低的误比特率，此后随着SNR的不断增大，常规FH的误比特率一直稳定在10－2数量级，而认知FH的误比特率则在13 dB时可以达到10－5数量级。因此，认知FH具有比常规FH更良好的抗单频干扰性能。

2)抗多频干扰性能

假设认知 FH系统与常规 FH系统在30 MHz，40 MHz，50 MHz，60 MHz，70 MHz等 5 个信道处受到多频干扰，其误比特率随信噪比SNR变化的曲线如图3所示。

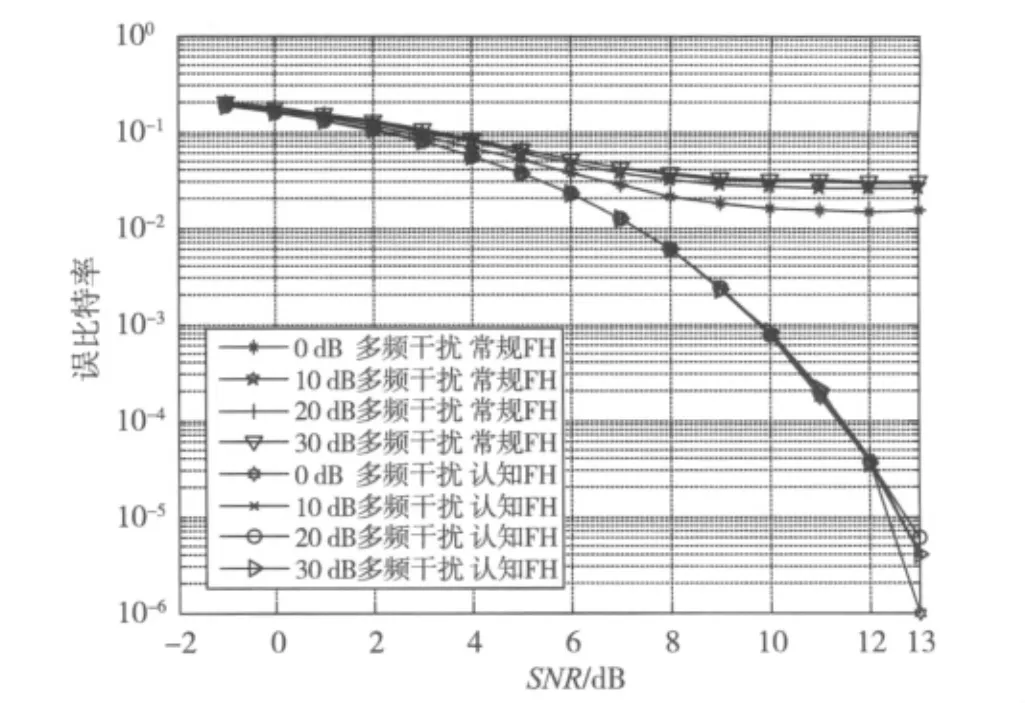
图3 多频干扰下认知FH与常规FH的误比特率曲线

从图3可以看出，从SNR=2 dB之后，认知FH较常规FH具有更低的误比特率，此后随着SNR的不断增大，常规FH的误比特率一直稳定在10－1数量级左右，而认知FH的误比特率在信噪比为10 dB时就达到10－3数量级，在信噪比为13 dB时达到10－5数量级。因此，认知FH具有比常规FH更佳的抗多频干扰性能。

3)抗部分频带干扰性能

假设认知FH与常规FH受到干扰因子分别为ρ=0.3和ρ=0.5的部分频带干扰，且信干比均为20 dB，其误比特率随信噪比SNR变化的曲线如图4所示。从图4可以发现，在同等干扰条件下，常规FH的误比特率为10－1数量级，已不能满足通信时需要的10－4～10－3数量级要求;而认知FH由于规避了干扰的信道，其误比特率在信噪比为9 dB之后就达到了10－3数量级，在13 dB时达到10－5数量级，表现出良好的抗部分频带干扰性能。

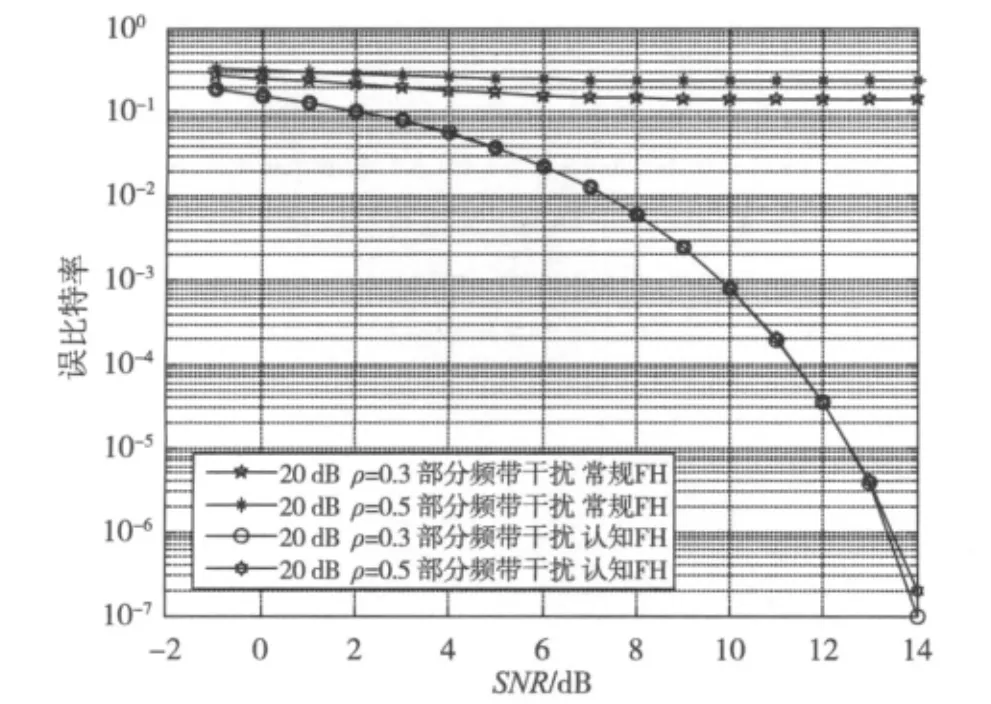
图4 部分频带干扰下认知FH与常规FH在不同干扰因子ρ下的误比特率曲线

假设在干扰因子ρ大小一定、信干比不同的情况下，认知FH和常规FH的误比特率随信噪比变化的曲线如图5所示。

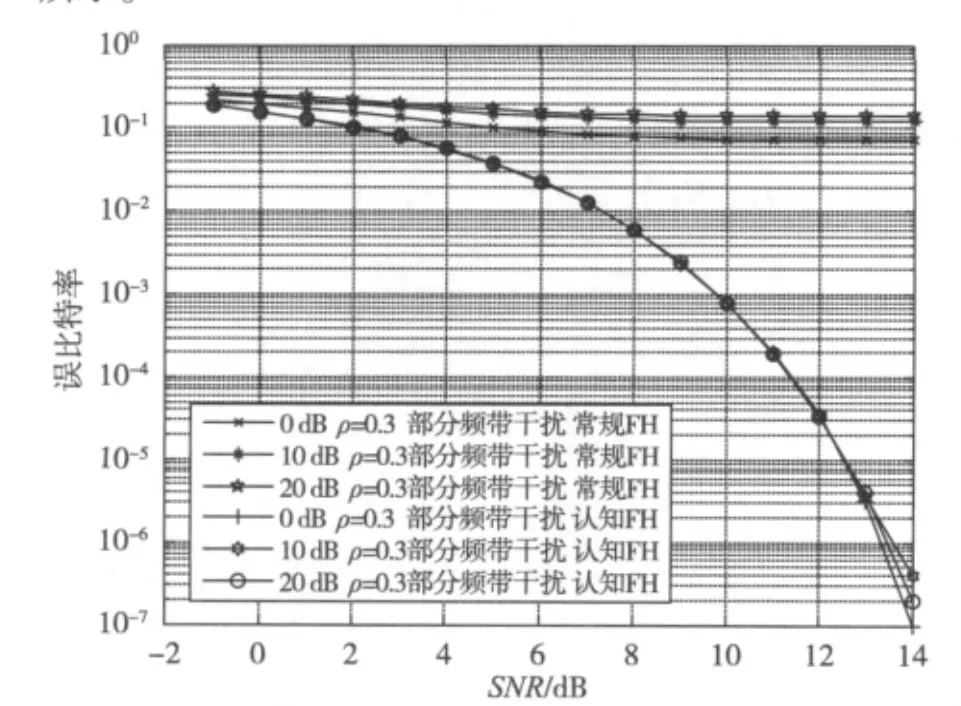
图5 部分频带干扰下认知FH与常规FH在不同信干比下的误比特率曲线

从图5中可以看出，常规FH的误比特率随着信干比的增大而增加，而认知FH的性能则不受信干比的影响，其抗干扰性能在信噪比为10 dB之后就维持在10－3的数量级以下，并随着信噪比的增大而不断减小，表现出良好的抗干扰性能。

4 小结

本文首先研究了认知FH通信系统的一种实现方案，并对其在单频干扰、多频干扰和部分频带干扰下的抗干扰性能进行了理论分析，并进行了性能仿真。通过仿真发现，与常规跳频相比，这种新的通信方案在同等的干扰条件下具有更低的误比特率。由于本文是假定对周围频谱已经实现准确感知和通信过程已实现理想同步和感知信息共享，因此，下一步将针对如何实现干扰实时而准确的感知和通信双方感知信息的交互作深入研究。

[1]尚佳栋，周倩，王祖林，等.基于自适应波束形成的抗干扰跳频通信方案[J].电光与控制，2011，18(4):18－20.

[2]郭丽华，穆晓敏，朱春华，等.一种新的自适应跳频通信系统[J].电讯技术，2009(2):19－23.

[3]CHEN Z，LI S，DONG B.Multi－user performance analysis of differential frequency hopping system over Rayleigh－fading channel[J].High Technology Letters，2008，14(2):147－153.

[4]GEIRHOFER S，SUN J Z，TONG L，et al.Cognitive frequency hopping based on interference prediction:theory and experimental results[J].Mobile Computing and Communications Review，2009，13(2):49－61.

[5]ZHI Rongxin，ZHANG Luyong，ZHOU Zheng.Cognitive frequency hopping[C]//Proc.3rd International Conference on Cognitive Ratio Oriented Wireless Networks and Communications，2008.CrownCorn:IEEE Press，2008:1－4.

[6]BROWN C，VIGNERON P J.Robust frequency hopping for high datarate tactical communications[EB/OL].[2012－07－01].http://oai.dtic.mil/oai/oaiverb=getRecord＆metadataPrefix=html＆identifier=ADA521139.

[7]郭亮，孙诚超，周超.一种新的跳频序列集构造方法[J].电视技术，2011，35(11):91－93.

[8]陈亚丁，刘晓晖，程郁凡，等.超高速跳频通信系统的实现及抗干扰性能[J].电子与信息学报，2007，29(9):2191－2194.