一种基于最小交叉熵的Canny边缘检测算法

陈世文，刘越畅

(嘉应学院计算机学院，广东 梅州 514015)

边缘是图像中的一种基本特征，可以为图像分析和图像识别提供重要的信息，是一个非常重要的研究课题。像素灰度值两边有着明显的变化表现为阶跃性边缘;灰度值处在从增加到减少的变化转折点表现为屋顶状边缘。传统的边缘检测算法有Robert算子、Prewitt算子、Sobel算子、LOG算子、Laplacian算子、Kirsch算子等。这些算子的基本特点是计算简单、实现容易，但是由于边缘本身的复杂性，这些算子在抗噪性能方面效果不够理想。很多学者提出了改进的边缘检测方法[1－6]，包括基于小波变换的边缘检测，基于数学形态学的边缘检测，基于分形几何的边缘检测等新的方法。

相对而言，Canny算子在边缘检测中具有较高的精度，因而得到了广泛的应用。但是由于Canny算子自身的不足，高低阈值需要人为确定、高斯滤波参数选择困难，容易造成检测中出现大量虚假边缘。有学者提出用OTSU算法计算Canny参数的门限阈值、在Canny算法中融入小波变换等改进方法[7－9]。针对Canny算子的不足，本文提出一种融入最小交叉熵的边缘检测算法，利用最小交叉熵动态地计算图像的高低阈值，解决图像的灰度级集中在某一区域时的情况;利用图像灰度的均值和方差计算Canny算子的高斯滤波参数。实验对比了本文算法与传统算法和文献[9]所采用的算法的检测结果，结果表明本算法边缘检测较好，噪声抑制能力较理想。

1 传统Canny算法

Canny算子在边缘检测中基于以下的最优准则:1)信噪比准则，即将非边缘点误判为边缘点或者将边缘点误判为非边缘点的概率要低;2)定位精度准则，即检测出的边缘位置尽可能地接近真正边缘中心点;3)单边响应准则，即单一边缘响应唯一，虚假边缘响应受到最大的抑制。

利用二维高斯函数构造滤波器，公式如下

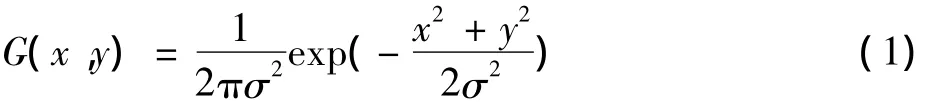
计算二维滤波器模板的一阶偏导，得到两个一维滤波器，用标准卷积得到高斯平滑。其中σ是高斯函数的标准差，控制着平滑图像的程度。

图像平滑后其梯度幅值和方向一般通过2×2邻域内的一阶导数的有限差分来计算。在x方向和y方向的偏导数分别为Px(x，y)和Py(x，y)，则图像的梯度幅值和梯度方向分别为

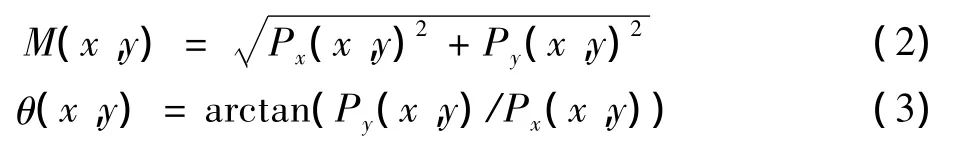
对像素点的梯度幅值进行非极大值抑制，即判断像素点的梯度值在其八邻域内是否为最大值，如果是，则是边缘，否则为零。

经过非极大值抑制后，Canny算子采用双阈值(高低阈值)方法检测图像边缘。

传统Canny算法的不足:使用单一的阈值对图像进行边缘检测，对直方图双峰不明显的图像检测效果不好，对含有噪声的图像容易误检错检。阈值的太大或者太小都影响边缘的检测效果。

2 最小交叉熵阈值法

假若一幅图像的尺寸为M×N，其灰度级为L，图像上某一像素点的灰度值表示为f(x，y)(1≤x≤M，1≤y≤N)，计算每个像素点在其K×K邻域的平均灰度值，得到一幅平滑的图像g(x，y)，其灰度级也为L。通常L取为255，K取为3，即8邻域模板。f(x，y)与 g(x，y)组成二元组记为(i，j)，设图像中灰度级为i邻域平均灰度级为j的像素点个数为r(i，j)，定义二元组(i，j)在图像和其邻域平滑图像中出现的概率为

定义二维直方图如图1所示，横坐标为图像像元的灰度值i，纵坐标为像元邻域平均灰灰值j，设阈值(S，T)(0≤S，T≤L－1)把二维直方图分割成A，B，C，D等4个区域，区域A和B分别代表目标和背景，区域C和D分别代表边缘或噪声，由于边缘和噪声较少，一般认为远离对角线区域的C和D的分量近似为零。如图1所示，任意阈值向量(S，T)对图像进行分割，可以得到目标和背景两类区域，分别标记为Ca和Cb，则两类区域的先验概率分别表示为

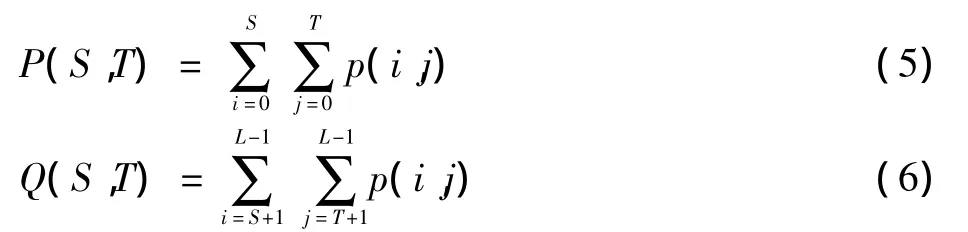
假设阈值为(S，T)时，目标和背景的类内均值分别表示为uP(S，T)和uQ(S，T)，其分别代表分割后目标和背景的灰度，则

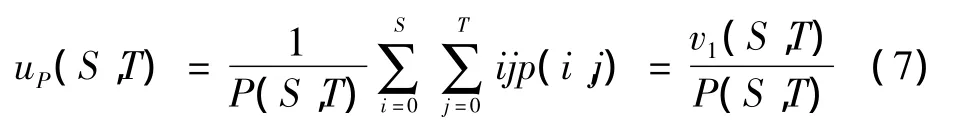
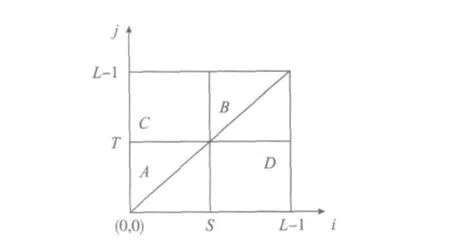
图1 二维直方图区域划分

最小交叉熵阈值法是图像分割中计算阈值的方法，考虑了图像中周围像素的相关性，可以动态地计算图像的分割阈值，用于计算Canny算子的高低阈值，满足复杂图像边缘检测的阈值要求。

3 滤波参数选取

对图像进行平滑滤波有利于抑制噪声，提高信噪比。高斯滤波器中高斯参数σ决定着滤波器抑制噪声的能力。高斯参数σ偏大，抑制噪声能力强，但是可能会把目标边缘细节信息滤除掉;若高斯参数σ偏小，又容易出现虚假边缘。这里，采用以下公式计算σ[6]

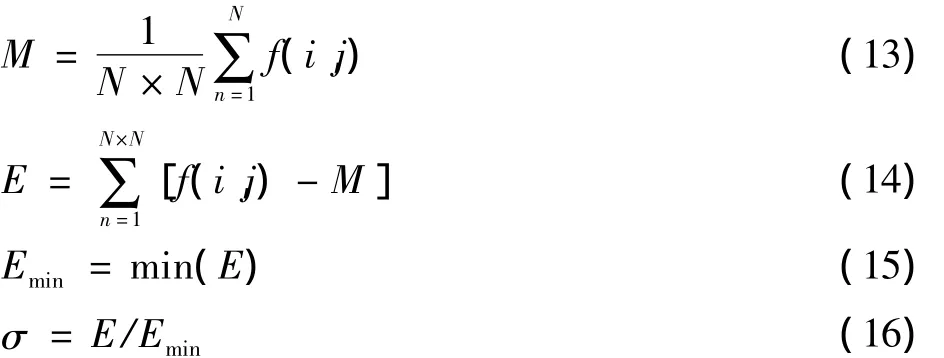
式中:N为窗口大小;M和E分别为图像的均值和方差;Emin为一幅图像中的最小方差。当σ值较大时，改为σ=kE/Emin，其中k=1/M，即为窗口内均值的倒数。采用方差计算σ，原因是方差较好地表征了窗口内的像素变化特点，通常方差小的为非边缘点或者是被噪声污染的小区域。

4 实验结果及分析

在MATLAB 7.1环境进行仿真实验，对3幅图像进行实验，利用最小交叉熵算法计算高阈值Th，为了节省计算，Tl为高阈值的一半。

如图2所示，给图2a加了0.01标准差的高斯噪声，由实验图可见传统的Canny算子检测效果不够好，对噪声的抑制能力较差。高斯滤波参数σ的选取很重要，若σ选取较大时，高斯平滑模板变大，频带窄，抗噪能力较强，但是容易造成图像的缓变边缘丢失及过度光滑;若σ选取较小时，频带较宽，边缘细节精度高，但是图像平滑作用较小，抗噪声能力较弱。

图2 Lena实验图

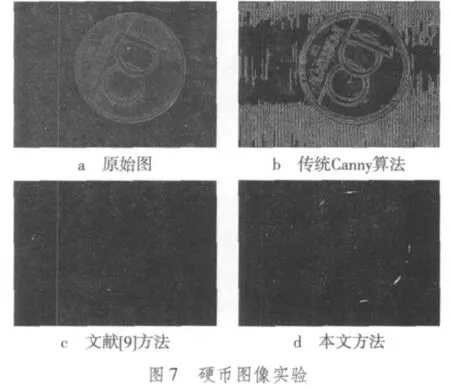
如图3所示，图3a为原始图，图3b为传统Canny检测结果，图4为硬币直方图。由图可见，检测效果较差，原因是传统的Canny算法采用确定的高低阈值，当图像的灰度级集中在某一区域时，直方图没有明显双峰，固定的高低阈值无法满足检测要求。高低阈值的选取很重要，高阈值关系到边缘检测的起始点，当高阈值Th较小时，检测到的边缘信息较多，但是虚假也随之增多;当高阈值Th较大时，抑制噪声能力增强，但是容易丢失实际边缘信息。低阈值Tl关系到边缘检测的中止点，Tl选择越小保留的边缘信息越多，随着Tl的增大，目标边缘信息不断减少，容易导致边缘的断裂。

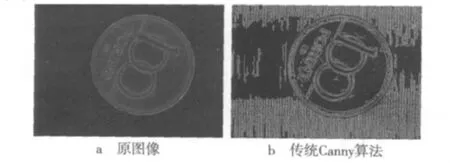
图3 硬币实验图

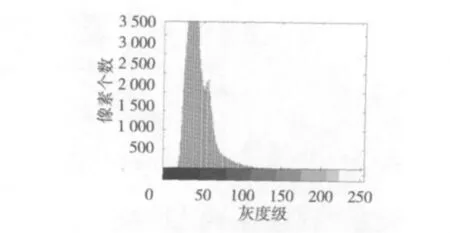
图4 硬币直方图

实验分别对几种情况进行实验:如图5所示，为直方图双峰比较明显的原始图;如图6所示，为加了0.01标准差的高斯噪声的图像;如图7所示(直方图如图3)，为直方图双峰不明显的图像。图5结果所示，当图像直方图双峰比较明显时，传统Canny算法检测的边缘信息丰富，但也有相当一部分虚假边缘，文献[9]方法大体检测出了边缘信息，但是在单车的后轮边缘信息丢失较严重，本文方法较好地检测出了目标边缘。图6结果所示，当图像被噪声污染时，传统Canny算法检测效果不理想，抑制噪声能力较差，文献[9]抑制噪声效果不错，但同时又丢失了部分边缘信息，本文方法抑制噪声能力较好，仍然能够检测出目标的轮廓。图7结果所示，当图像灰度级集中时，即直方图双峰不明显时，传统Canny算法出现大量虚假边缘，效果不理想，文献[9]对单峰的直方图的边缘检测效果亦不理想，本文方法虽然也丢失了一些边缘信息，但是大体上检测出了目标边缘，结果仍算满意。因此，本文方法相对传统Canny算法具有一定优越性，比文献[9]算法好。

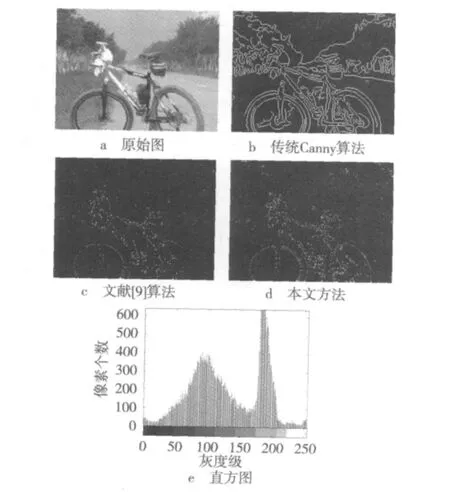
图5 单车图像处理结果

5 结论

本文针对传统Canny算法在边缘检测中的不足，提出了一种基于最小交叉熵的Canny边缘检测算法。传统Canny算法容易检测到虚假边缘，本算法通过最小交叉熵来计算Canny的高低阈值，利用灰度值来计算高斯参数σ，较好地解决了边缘误检错检的情况。实验证明，算法抑制噪声能力较强，对于灰度级集中的图像亦能检测出大体轮廓，算法优于传统Canny算法。

[1]ZHANG Bin，HE Saixian.Improved edge detection method based on Canny algorithm[J].Infrared Technology，2006，28(3):165－169.

[2]CHEN Jie，WANG Zhenhua，DOU Lihua.Scale adaptive Canny edge detection method[J].Opto－Electronic Engineering，2008，35(2):79－84.

[3]柴俊华，应骏.基于Canny算子的图像轮廓提取的改进方法[J].电视技术，2008，32(S1):48－50.

[4]黄剑玲，郑雪梅.一种改进的基于Canny算子的图像边缘提取算法[J]. 计算机工程与应用，2008，44(25):170－172.

[5]LI C H，LEE C K.Minimum cross entropy threshold[J].Pattern Recognition，1993，26(4):617－625.

[6]薛丽霞，李涛，王佐成.一种自适应的Canny边缘检测算法[J].计算机应用研究，2010，27(9):3588－3590.

[7]黄剑玲，陈博政.一种基于Canny的边缘检测优化算法[J].计算机仿真，2010，4(27):252－255.

[8]白婷婷，邓彩霞，耿英.基于小波变换与Canny算子融合的图像边缘检测方法[J]. 哈尔滨理工大学学报，2010，2(15):44－47.

[9]李华强，喻擎苍，方玫.Canny算子中Otsu阈值分割法的运用[J].计算机工程与设计，2008，5(29):2297－2299.