正交机器人机构工作空间的数值算法

张建业，赵 臣，张宏杰，张大卫

正交机器人机构工作空间的数值算法

张建业1,2，赵 臣1，张宏杰1,2，张大卫1

(1.天津大学机械工程学院，天津 300072；2.天津工业大学机械工程学院，天津 300387)

提出了一种计算n自由度正交机器人机构工作空间的数值方法．先求出机器人机构末端两个关节对应子工作空间的边界曲面，在前一个关节建立参考坐标系，将已知子工作空间的边界曲面分成若干层，求出每一层上的截交线，定义截交线的两个端点、半径坐标值最大点和最小点等为特征点，根据这些特征点可生成前一级子工作空间的边界曲线和边界曲面，由此递推可生成工作空间的边界曲面，并计算出工作空间的体积值．以三自由度正交机器人机构为例进行了仿真分析，结果表明该算法具有运动学计算量小、结果精确等优点．

正交机器人机构；工作空间；子工作空间；特征点

工作空间是机器人机构非常重要的设计参数和运动学特性，对机器人的优化设计、轨迹规划与运动控制等过程非常重要．目前，工作空间的求解方法可以分为3种：几何法、数值法和解析法[1-4]．几何法是以剖切面或剖切线来表示工作空间的，具有直观性强、结果精确等优点，但只适用于自由度较少、工作空间为简单几何体的情况．解析法需要建立工作空间边界曲面的解析方程，由于机器人机构运动学本身的非线性、复杂性，对于多自由度机器人机构而言，边界曲面方程往往十分复杂，不适应于工程应用．数值法是用离散化的方法近似求解工作空间的边界曲线和边界曲面，具有简单灵活、易于编程等优点，非常适用于多自由度机器人机构．随着计算机技术的发展，工作空间的数值解法显示出巨大的优越性，国内外学者对此进行了广泛的研究．Rastegar等[5]提出用蒙特卡洛随机取样的方法和机构正运动学获得一些简单机构的近似工作空间和边界曲面，Choi等[6]提出了一种易于编程的工作空间边界搜索算法，以在一组平行平面上搜索到的截面曲线代表工作空间边界，搜索过程分为2步：第1步用线性运动学模型对下一个边界点进行估计；第2步通过模糊优化方法找到精确点，最后以一个限制了关节角度范围的六自由度机构为例进行了说明，用曲面重构的方法建立了工作空间边界的曲面模型．王兴海等[7]提出了一种可计算任意自由度串联机器人机构工作空间的数值方法，以极值理论和优化方法为基础，把确定机器人机构边界曲线和边界曲面的问题转化为求解满足一定约束条件的极值问题，通过计算工作空间的极限距离，求出机器人工作空间边界曲面上的一系列特征点，用这些点连成线和面表示出机构的工作空间．曹毅等[8]采用蒙特卡罗方法，根据机器人关节空间到工作空间的运动学映射关系，获得了由随机点构成的机器人工作空间，采用按列划分的方法，求出了平面机构工作空间的边界曲线以及对应的面积表达式，按照按层划分的方法，获得了三维工作空间边界曲面的形状和体积．

笔者根据机器人机构子工作空间的定义，提出了一种递推求解n自由度正交机器人机构工作空间的数值方法，将已知子工作空间边界曲面分成若干层，定义了前一级子工作空间边界曲面的特征点，由此构造其边界曲线和边界曲面，最后构造了工作空间的边界曲线和边界曲面，并计算出工作空间的体积值，以三自由度正交机器人机构为例进行了仿真分析．

1 机器人机构工作空间

1.1 正交机器人机构

目前，大多数工业机器人机构为Unimation公司的PUMA型，具有6个转动关节，采用了位置和姿态解耦的设计，其工作空间由前3个关节确定，第一个关节的轴线为竖直方向，第二、第三关节的轴线为水平方向，且互相平行，这种机构称为平行机构，后3个关节轴线垂直相交于一点[9]．另一种机器人机构为ABB公司的IRB 6400C型，其前3个关节采用了相邻关节轴线互相垂直的设计，这种机构被称为正交机器人机构，如图1所示，其运动学参数见表1．正交机器人机构的工作空间比平行机构的工作空间更加复杂，其求解算法也更具有普遍性和适用性，因此，本文中选择以正交机器人机构的工作空间为分析对象．

图1 三自由度正交机器人机构运动学示意Fig.1 Schematic representation of 3R orthogonal manipulator

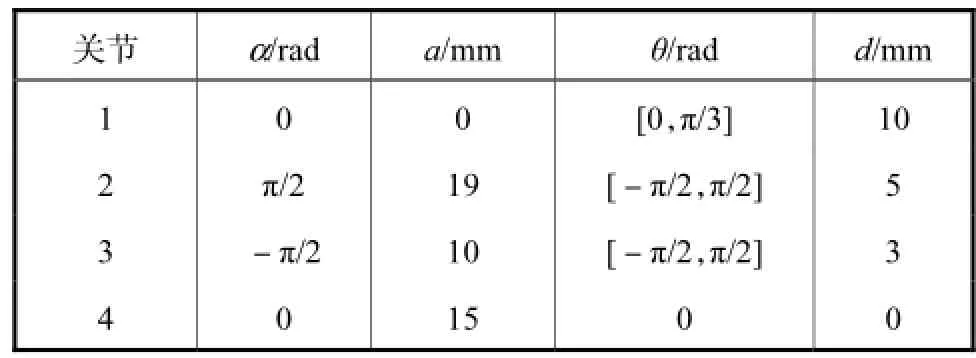
表1 三自由度正交机器人机构的运动学参数Tab.1Kinematic parameters of 3R orthogonal manipulator

1.2 机器人机构工作空间的描述

一般地，n自由度机器人机构的运动学方程可以描述为

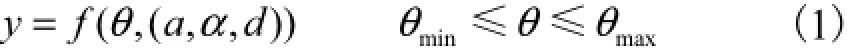
式中：θ表示关节变量；θmin表示运动范围的下界；θmax表示运动范围的上界．

机器人机构的工作空间可以定义为不同关节变量所达到的末端参考点的所有位形的集合，机器人机构的工作空间可以由关节空间和上述运动学映射定义为

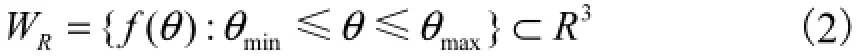
给定了机器人机构的杆件几何参数后，机器人工作空间就由关节变量的活动范围确定，由于实际结构和驱动装置的限制，关节变量只能在一定范围内取值，增加了求解工作空间的复杂性．作为一个空间体积，工作空间具有一定的边界曲面或边界线，目前，工作空间的研究内容主要为工作空间的边界、工作空间的形状和体积、空洞和空腔等[9]．

2 正交机器人机构工作空间求解

2.1 工作空间的边界曲线和边界曲面

首先，应该对n自由度正交机器人机构工作空间的特征及其形成过程进行分析和总结，对于3自由度正交机器人机构，其工作空间可以看作是由关节2和关节3在其角度范围内运动生成的圆环面绕关节1轴线旋转后生成的，对于k自由度正交机器人机构，固定其第一个关节，则可以把其当作一个k-1自由度正交机器人机构，假设该k-1自由度正交机器人机构的工作空间已知，将其绕关节1轴线旋转后，就可以得到k自由度正交机器人机构的工作空间，通过递推，可得到n自由度正交机器人机构的工作空间．

求解n自由度正交机器人机构工作空间边界曲线和边界曲面的主要步骤如下．

(1) 假设n自由度正交机器人机构的前k个关节相对于基础坐标系固定，定义机器人机构末端参考点的所有位形的集合为第k级子工作空间，根据式(2)，kW可描述为[10]

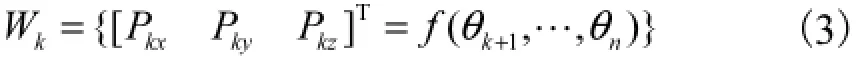
式中：[PkxPkyPkz]T为机器人末端参考点在第k个关节坐标系的坐标．

3 仿真分析

写成圆柱坐标形式为

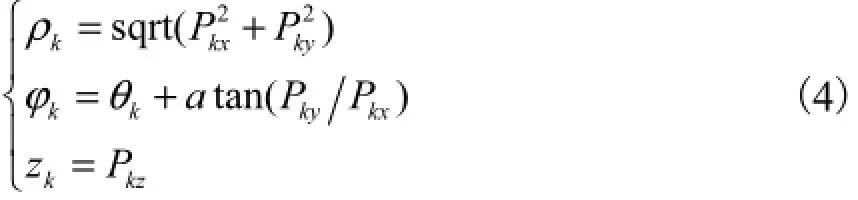
(2) 假定正交机器人机构末端两关节在其运动范围内转动，其余关节固定在参考位置，末端参考点的轨迹为一旋转曲面Sn-2，即第n-2级子工作空间Wn-2的边界曲面，用网格法生成旋转曲面S，以此作为求解工作空间的初始条件．

(3) 在关节k上建立圆柱坐标系，根据子工作空间Wk边界曲线的z轴坐标值范围，用一组平面将其分成若干层，并求出截交线，定义每一段截交线上的半径坐标值最大点、最小点和截交线的两个端点为第k-1级子工作空间边界曲线的特征点，建立特征点数组．

(4) 根据每段截交线上特征点的半径坐标值及关节k的角度运动范围，构造出与其对应的圆弧线，将每段截交线旋转复制到关节k角度最大的位置和最小的位置．

(5) 每一个平面上的截交线和对应的圆弧线都会构成一个或几个闭合连通区域，提取每个闭合连通区域的边界作为k-1级子工作空间的边界曲线．

(6) 根据k-1级子工作空间的边界曲线，生成其边界曲面Sk-1．

(7) 选择前一个关节，重复第3～第6步，直到生成正交机器人机构工作空间的边界曲线和边界曲面．

2.2 工作空间的体积

工作空间体积是机器人机构的一项非常重要的定量评价指标，也是机器人工作空间分析和综合、机构尺度设计、结构优化中需要精确计算的一项参数指标，在求解工作空间边界曲面的基础上，还需要进一步确定工作空间的体积．

求解正交机器人机构工作空间体积的问题可转化为求解平行截面面积已知的立体体积的问题，根据梯形积分法则，可计算出工作空间体积的近似值为

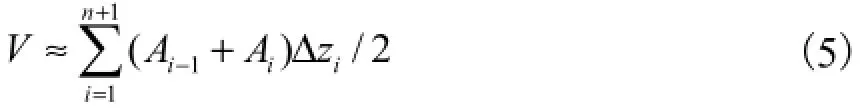
式中：Ai表示工作空间第i个截面的面积；Δzi为第i个截面与相邻截面的距离．当n足够大时，可获得工作空间体积的精确值．

为验证上述算法的有效性，编写了三自由度正交机器人机构工作空间的分析程序，流程如图2所示，该程序在输入三自由度正交机器人机构的运动学参数、网格数和分层数等参数后，可绘制出工作空间的边界曲线和边界曲面，计算出工作空间的体积．表2描述了子工作空间的分层数对体积值的影响．图3～图7描述了三自由度正交机器人机构边界曲线和边界曲面的求解过程．

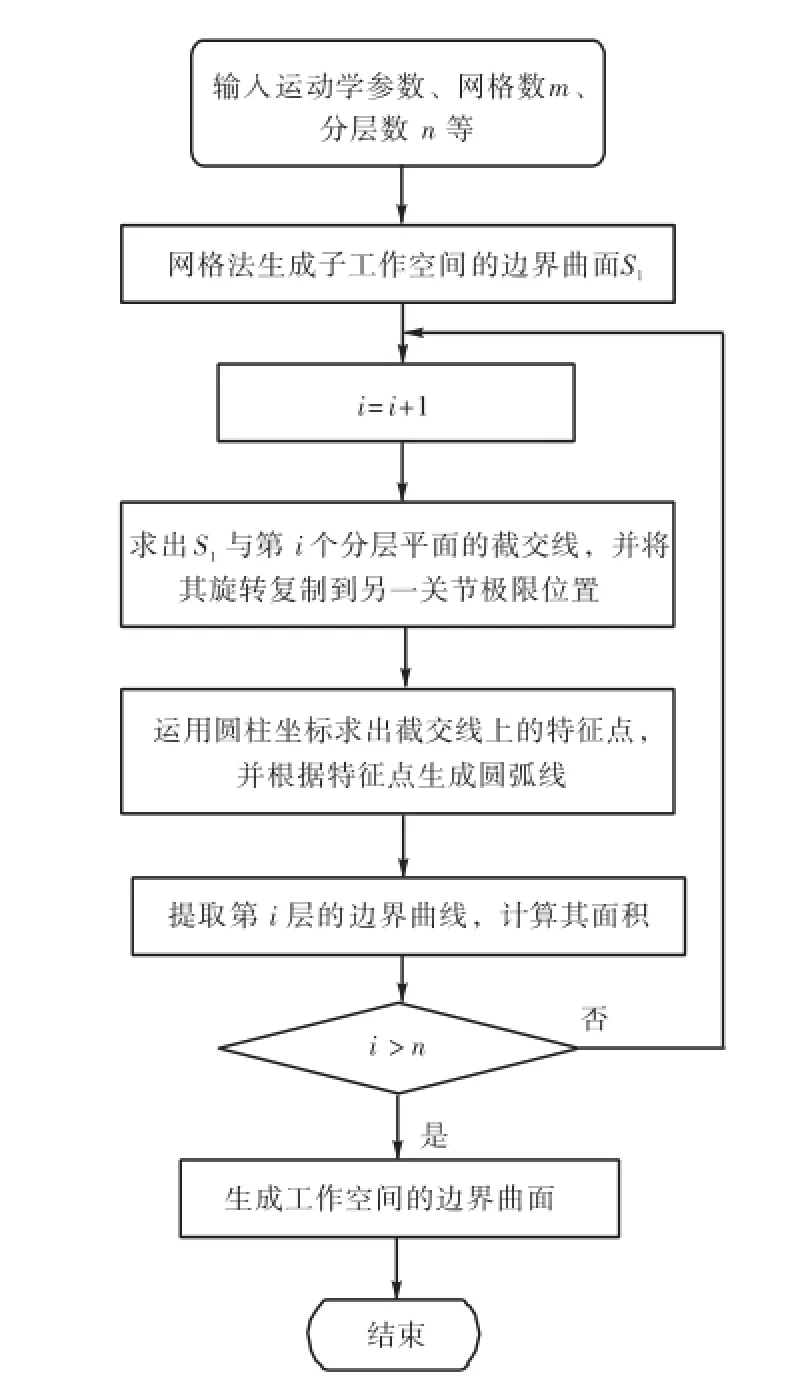
图2 工作空间边界曲面算法流程Fig.2 Flowchart for workspace boundary

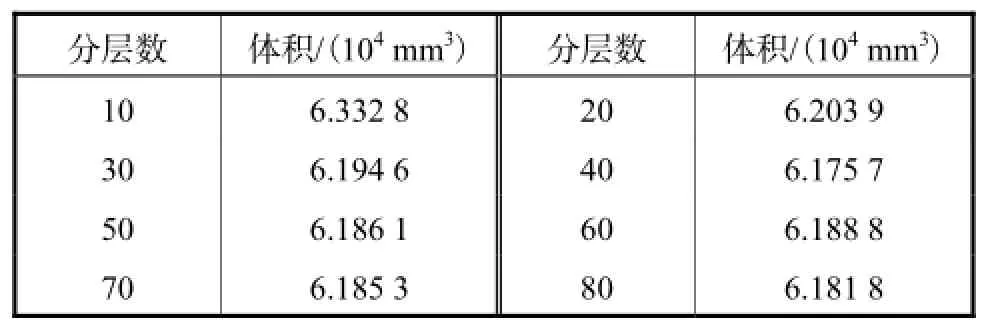
表2 三自由度正交机器人机构工作空间的体积Tab.2 Volume of 3R orthogonal manipulator

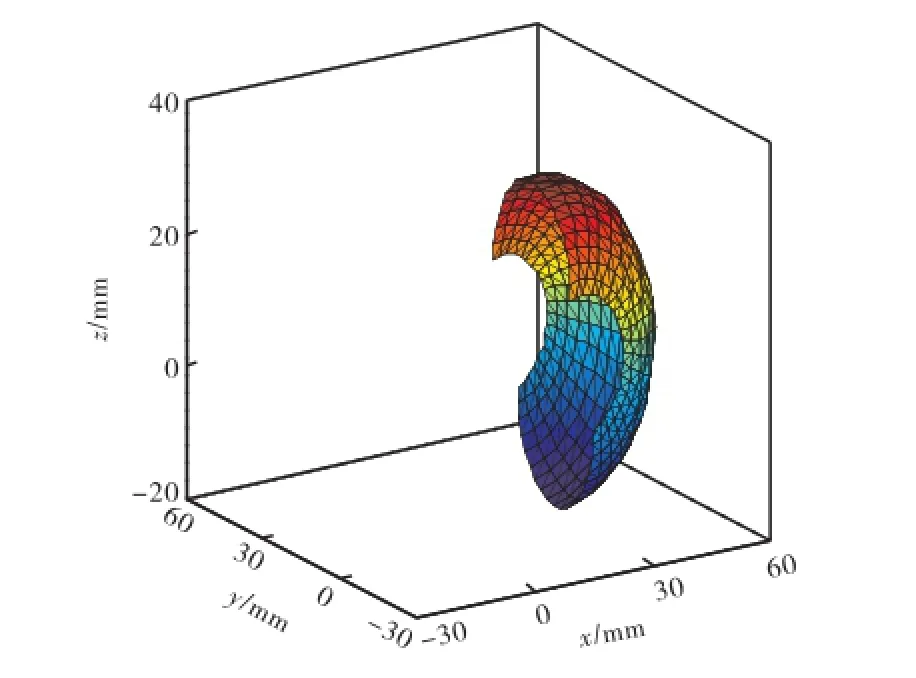
图3 1级子工作空间示意Fig.3 1sh sub workspace

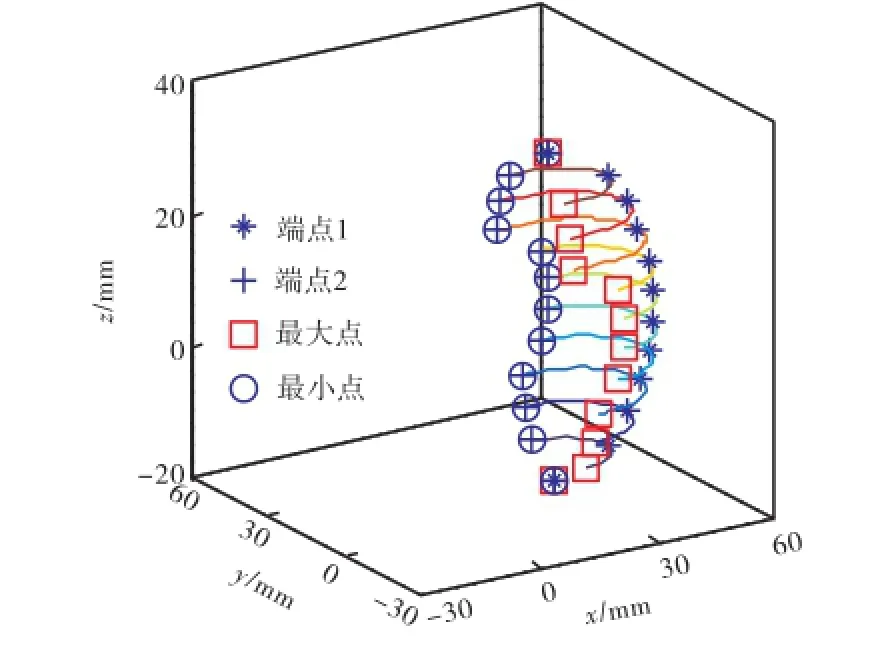
图4 子工作空间特征点示意Fig.4 Feature points of sub workspace

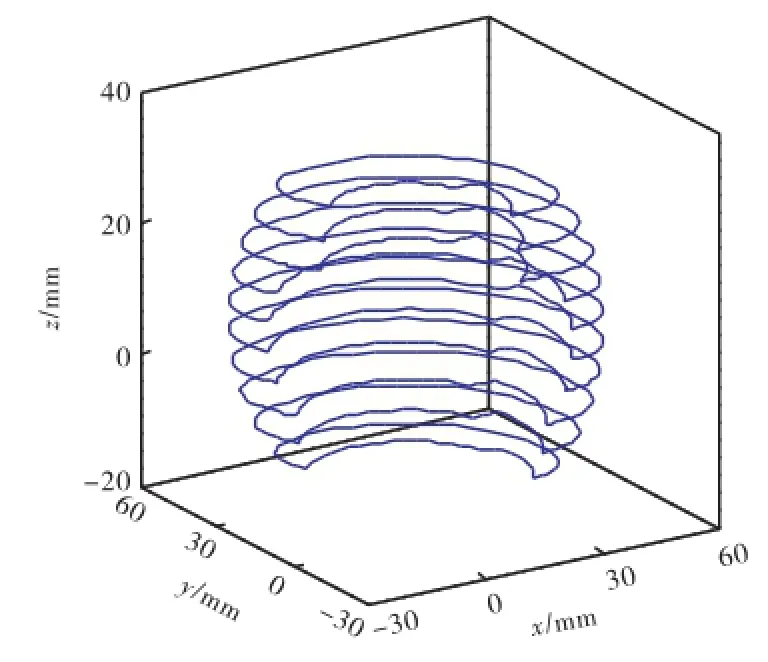
图5 截交线和圆弧线Fig.5 Cross section lines and arc lines

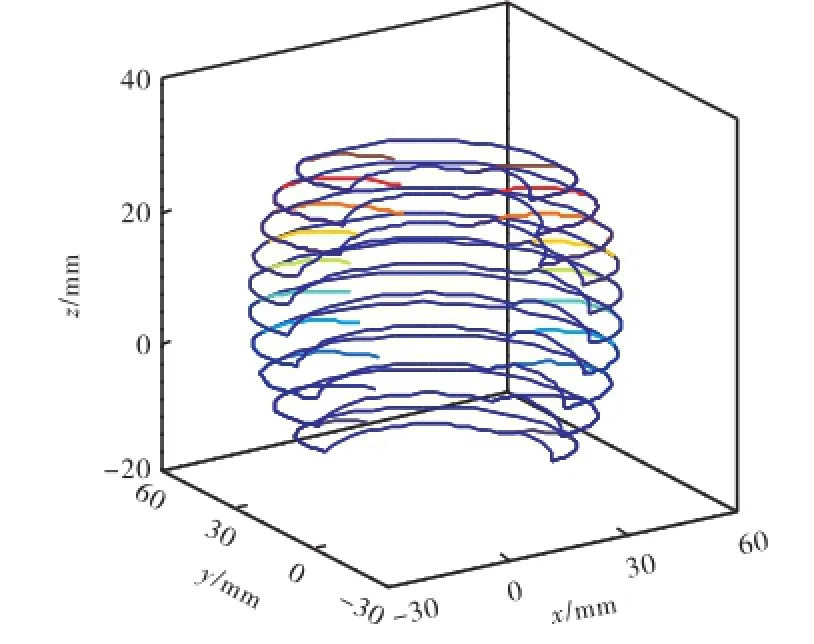
图6 工作空间边界曲线Fig.6 Workspace boundary curves

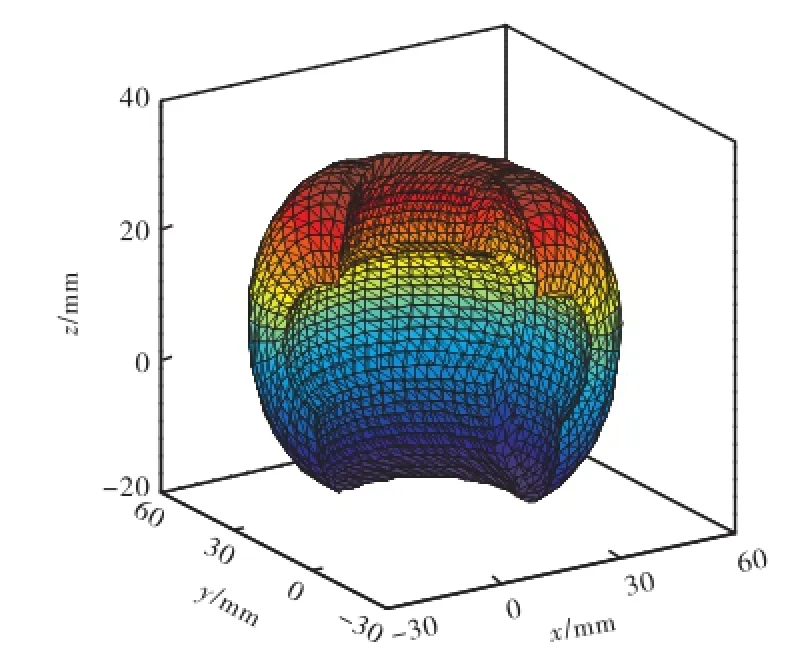
图7 工作空间边界曲面Fig.7 Workspace boundary surfaces

4 结 论

(1) 通过子工作空间的递推算法可以求解出n自由度正交机器人机构工作空间边界曲线和边界曲面．首先用分层法获得子工作空间的截交线，由截交线上的特征点生成圆弧线，提取每个平面上截交线和圆弧线构成的闭合连通区域的边界作为前一级子工作空间的边界曲线，并进一步构造出前一级子工作空间的边界曲面．该算法不需要复杂的优化算法，可大大减少运动学计算量．

(2) 求出每层平面上工作空间边界曲线的面积，根据梯形积分法则，在此基础上计算出工作空间体积的近似值，增加工作空间边界曲面的分层数，可使计算结果逐渐接近其理论值．

［1］ Marco Ceccarelli. A formulation for the workspace boundary of general N-revolute manipulators[J]. Journal of Mechanism and Machine Theory，1996，31(5)：637-646.

［2］ Tyapin I，Hovland G，Brogardh T. A geometrical method for calculating the unreachable workspace of the 3-DOF Gantry-Tau parallel manipulator[EB/OL]. http:// www.araa.asn.au/acra/acra2007/papers/paper176,final.pd f，2007-12-10．

［3］ Bulca F，Angeles J，Zsombor-Murray P J. On the workspace determination of spherical serial and platform mechanisms[J]. Mech Mach Theory，1999，34(3)：497-512.

［4］ Yang J，Abdel-Malek K，Zhang Y. On the workspace boundary determination of serial manipulators with nonunilateral constraints[J]. Robotics and Computer-Integrated Manufacturing，2008，24(1)：60-76.

［5］ Rastegar J，Perel D. Generation of manipulator workspace boundary geometry using the Monte Carlo method and interactive computer graphics[J]. Journal of Mechanical Design，1990，112(3)：452-454.

［6］ Choi C H，Park H S，Kim S H，et al. A manipulator workspace generation algorithm using a singular value decomposition[C]//International Conference on Control，Automation and Systems. Seoul，Korea， 2008：163-168.

［7］ 王兴海，周 迢. 机器人工作空间的数值计算[J]. 机器人，1988，9(1)：50-53.

Wang Xinghai，Zhou Tiao. Digital calculation of workspace for a robot manipulator[J]. Robot，1988，9(1)：50-53(in Chinese).

［8］ 曹 毅，李秀娟，宁 祎，等. 三维机器人工作空间及几何误差分析[J]. 机械科学与技术，2006，25(12)：1458-1502.

Cao Yi，Li Xiujuan，Ning Yi，et al. Computation and geometrical error analysis of a 3D robot’s workspace[J]. Mechanical Science and Technology，2006，25(12)：1458-1502(in Chinese).

［9］ Zein M，Wenger P，Chablat D. An exhaustive study of the workspace topologies of all 3R orthogonal manipulators with geometric simplification[J]. Mechanism and Machine Theory，2006，41(8)：971-986.

［10］ 潘汉军，汪钟正．工业机器人工作空间分析[J]. 武汉工业大学学报，1988，10(2)：237-244.

Pan Hanjun，Wang Zhongzheng. Analysis of manipulator workspace[J]. Journal of Wuhan University of Technology，1988，10(2)：237-244(in Chinese).

An Algorithm for Workspace of Orthogonal Manipulators

Zhang Jianye1,2，Zhao Chen1，Zhang Hongjie1,2，Zhang Dawei1
(1. School of Mechanical Engineering，Tianjin University，Tianjin 300072，China；2. School of Mechanical Engineering，Tianjin Polytechnic University，Tianjin 300387，China)

An algorithm for the workspace of nR orthogonal manipulators was developed. The sub workspace boundary surface of the last two joints was generated as initial sub workspace boundary, and the cross sections of the initial sub workspace boundary were created on the preceding joint coordinate. The two end points and the points with the maximum and minimum radius of each cross section curve were defined as feature points, based on which the boundary curves and the boundary surfaces of the former sub workspace were determined. And then the workspace was computed by this iterative process, and the volume of the workspace boundary was calculated. A simulation was performed on a 3R orthogonal manipulator. Simulation results show that the proposed algorithm has the advantages of small amounts of kinematic calculation and high precision.

orthogonal manipulators；workspace；sub workspace；feature point

TP24

A

0493-2137(2013)10-0862-05

DOI 10.11784/tdxb20131002