不同温度下钙基吸收剂煅烧反应动力学中的补偿效应
2013-06-04陈鸿伟陈江涛危日光陈龙
陈鸿伟,陈江涛,危日光,陈龙
(华北电力大学 能源动力与机械工程学院,河北 保定,071003)
随着温室效应的加剧,利用来源广泛、价格低廉的石灰石等钙基吸收剂循环煅烧/碳酸化反应分离燃煤电厂烟气中的CO2受到各国学者的普遍关注[1-3]。由于钙基吸收剂煅烧分解是后续脱碳反应的前提,而且分解情况将对脱除效果有着重大的影响。因此,许多学者对钙基吸收剂分解反应动力学特性进行了研究[4-6]。动力学补偿效应是动力学研究中的一个重要内容。动力学补偿效应是指在均相或多相的系列相关反应中,常会发现随着活化能的增减指前因子亦增减,即活化能与指前因子这2个对反应速率起着相反影响的动力学参数之间存在着相互补偿的关系。补偿效应出现的前提是同类物质的相似反应或不同反应条件下的同一反应,如在不同溶剂中的液相反应、催化剂组成有规律变化的催化反应或表面预处理不同的多相反应以及同类无机盐或有机高聚物的热分解反应等[7-9]。关于钙基吸收剂煅烧分解动力学补偿效应的研究较少,而且集中在改变升温率、样品质量、样品种类等反应条件下的补偿效应研究[10-11]。对于不同反应温度下的动力学补偿效应研究,目前未见此方面的报道。本文作者试图通过对分析纯 CaCO3和保定天然石灰石进行不同温度范围内的动力学分析,得到温度变化条件下二者补偿特性的差异,为更深入探讨钙基吸收剂分解规律提供新的途径。
1 实验部分
1.1 实验系统
整个实验在自建的热重分析仪上完成,其灵敏度为0.1 mg,称量范围±200 g,测温范围0~1 000 ℃,重复性实验误差±1%,满足实验精度要求。试样的热重数据由系统软件自动实时记录和保存,通过后续的数据处理软件得到转化率x-t曲线。吹扫气氛为N2,气体纯度大于99.9%,通过转子流量计控制N2流量。实验装置如图1所示。
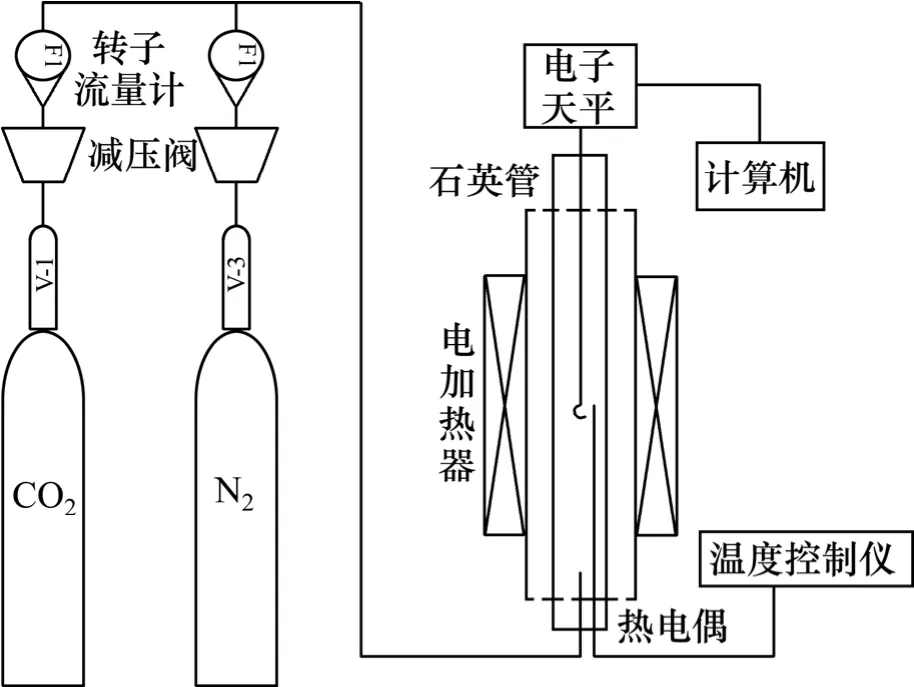
图1 实验装置图Fig. 1 Experimental apparatus
1.2 钙基吸收剂煅烧实验
实验在常压下进行,实验样品为分析纯CaCO3和保定天然石灰石,通过筛分取粒度在48~62 μm区间的颗粒。分析纯CaCO3技术指标如表1所示,石灰石的化学成分如表2所示。每次取用(0.3±0.02) g样品,煅烧气氛总流量1 000 mL/min。为减小样品颗粒间的扩散阻力,将样品平铺在坩埚底面,形成厚度均匀的薄层。为使实验过程更接近真实的反应过程,实验采用等温法。首先从热重分析仪底部通入N2排出石英管中的空气,然后打开温控仪升温至设定温度,待温度稳定后开始实验。
1.3 钙基吸收剂煅烧转化率的计算
钙基吸收剂煅烧转化率x为:
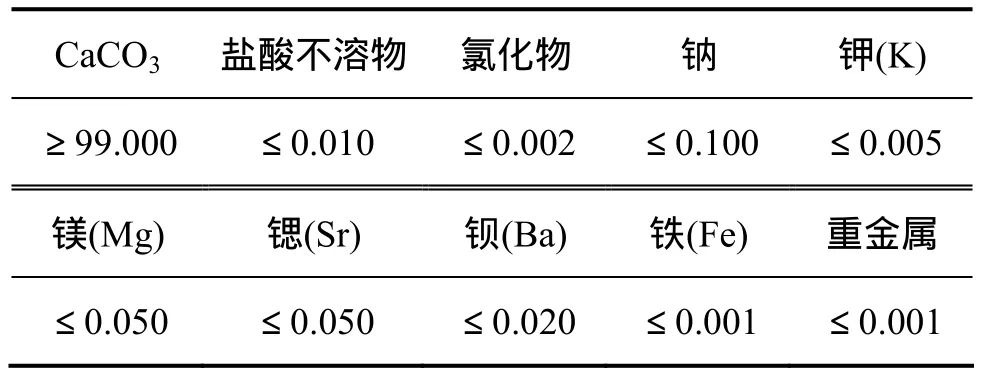
表1 分析纯CaCO3技术指标(质量分数)Table 1 Pure CaCO3 technology index %
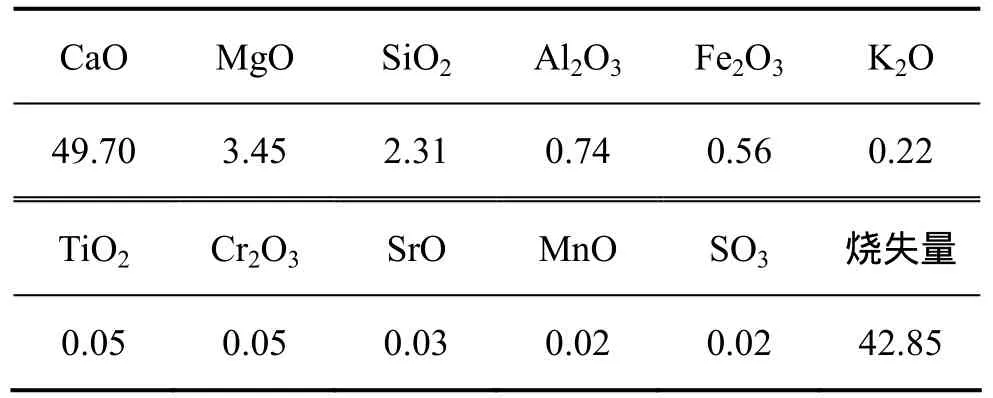
表2 石灰石样品化学的成分(质量分数)Table 2 Chemical composition of limestone %

其中:m0为反应前样品的质量;mt为反应进行时间 t后样品的质量;ma为样品完全煅烧后的质量。
为验证由质量–时间曲线所计算的转化率 x的准确性,利用单独的电子天平分别称量反应前后样品的质量,计算得到的转化率与利用质量–时间曲线计算的最终转化率结果一致,说明所得的转化率x准确可靠。
1.4 煅烧反应性能评价
采用反应性指数R定量的衡量不同温度下钙基吸收剂煅烧分解反应性,R越大表明钙基吸收剂分解反应性越好,具体的表达式为:

式中:τ0.5为钙基吸收剂煅烧转化率达到50%的时间。
2 结果与讨论
2.1 不同温度下钙基吸收剂的分解反应性
图2所示为钙基吸收剂分解反应性指数R随煅烧温度的变化情况。由图2可知:分析纯CaCO3和石灰石的反应性指数R在低温700 ℃时仅为0.054和0.077 min-1,而高温975 ℃时则分别升高至2.111和2.566 min-1,分别增长约39倍和33倍,说明温度对钙基吸收剂分解反应占据重要的影响,这是因为钙基吸收剂煅烧反应为吸热反应,反应温度越高,分解反应越快。在700~825 ℃范围内,分析纯CaCO3和石灰石分解反应性指数基本相同,石灰石略高于分析纯CaCO3,说明低温严重影响了分解反应过程的进行,不同钙基吸收剂分解反应的异同不宜在此温度段内比较。825~975 ℃范围内,温度对分解反应的阻碍作用基本消除,分析纯CaCO3和石灰石在此温度段内分解反应性指数快速升高,且石灰石的分解反应性指数高于分析纯CaCO3,说明石灰石的分解活性比分析纯CaCO3的高。

图2 反应性指数随煅烧温度的变化Fig.2 Variations of reactivity index with different temperatures
通过对比石灰石和分析纯CaCO3的成分可知,石灰石中含有较多的 MgCO3,Al2O3,Fe2O3以及 K2O等,这些杂质的存在对石灰石的分解反应有一定的影响。文献[12]指出:由于石灰石中 MgCO3和 CaCO3交错存在,在较低的温度下 MgCO3首先分解放出CO2,在石灰石的周围形成孔隙,使得较高温度下石灰石分解反应的固体扩散阻力减小而分解加快。文献[13]通过分析添加K和Na化合物的CaCO3具有较高的分解速率,推断其机理可能是K和Na化合物能与CaO等形成低熔点共融物,使 CaO产物层的孔隙增加,减少了CO2扩散阻力。因此,可以认为正是由于石灰石中杂质的存在,通过改变分解产物空隙结构加速了分解反应,致使石灰石活性高于分析纯CaCO3。
2.2 动力学参数的计算
等温法求取动力学参数通常由动力学方程(3)和经典的Arrhenius式(4)联立求解,其中f(x)为反应机理函数,不同化学反应机理有不同表达形式;k0为表观指前因子,E为表观活化能,R为摩尔气体常数。动力学参数计算主要有积分法和微分法,本文采用积分法,通过对式(3)进行积分得到式(5),
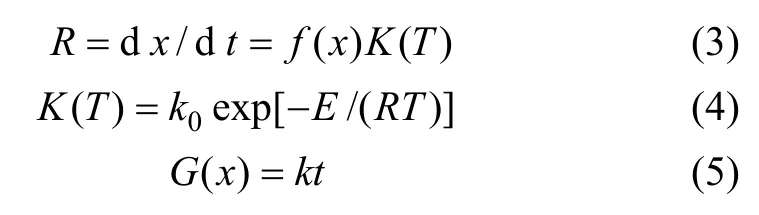
其中:G(x)为积分形式的机理函数,k为反应速率常数。根据实验数据和不同的机理函数,回归得到 G(x)与 t直线关系,通过比对相关系数可以确定反应最佳机理函数f(x)。同时,由G(x)与t回归直线斜率得到不同温度下反应速率常数k,对式(4)两边取自然对数,由ln k-1/T拟合曲线并由斜率和截距分别得到表观活化能E和指前因子k0。
为了得到动力学参数随温度的变化规律,在700~975 ℃范围内每间隔 25 ℃分别得到分析纯CaCO3和石灰石煅烧转化率曲线,依次分别对3个温度点进行动力学分析,得到不同温度范围的动力学参数。为了便于对比分析纯CaCO3和石灰石分解反应的动力学参数,假定一定温度范围的平均温度为特征温度,便可得到动力学参数随温度的变化曲线。
选取了 42种常用动力学机理函数[13],包含了扩散机理、成核生长机理、相边界反应机理及幂定律等常用机理函数。通过编程分别计算了不同机理函数下G(x)与 t回归直线的相关系数和截距,通过比对相边界反应(圆柱形对称)机理函数下分析纯CaCO3和石灰石在各温度下的相关系数r分别大于0.994和0.989,较适合N2环境气氛下CaCO3热分解,这与文献[14-15]研究一致。在机理函数确定的基础上,编程计算了不同温度范围内的动力学参数,如图3~5所示。
2.3 不同温度下钙基吸收剂的分解反应速率常数
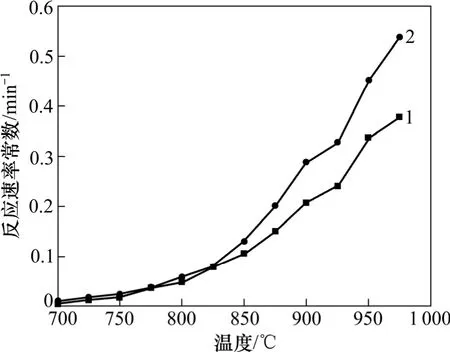
图3 反应性速率常数随煅烧温度的变化Fig. 3 Variations of reactive rate constant with different temperatures
图 3所示为相边界反应(圆柱形对称)机理函数下反应速率常数k随煅烧温度的变化规律。对比图2和图3可知:反应速率常数k与反应性指数R随温度变化规律一致,均呈现类似抛物线的增长规律。反应性指数R的计算不涉及机理函数的选择,而反应速率常数的计算是在最佳机理函数确定的基础上进行。二者均是表征钙基吸收剂分解反应快慢的指标,二者变化规律的一致性间接说明了机理函数选择的正确性。
2.4 不同温度下钙基吸收剂的分解动力学参数

图4 温度对表观活化能的影响Fig. 4 Effects of temperature on apparent activation energy
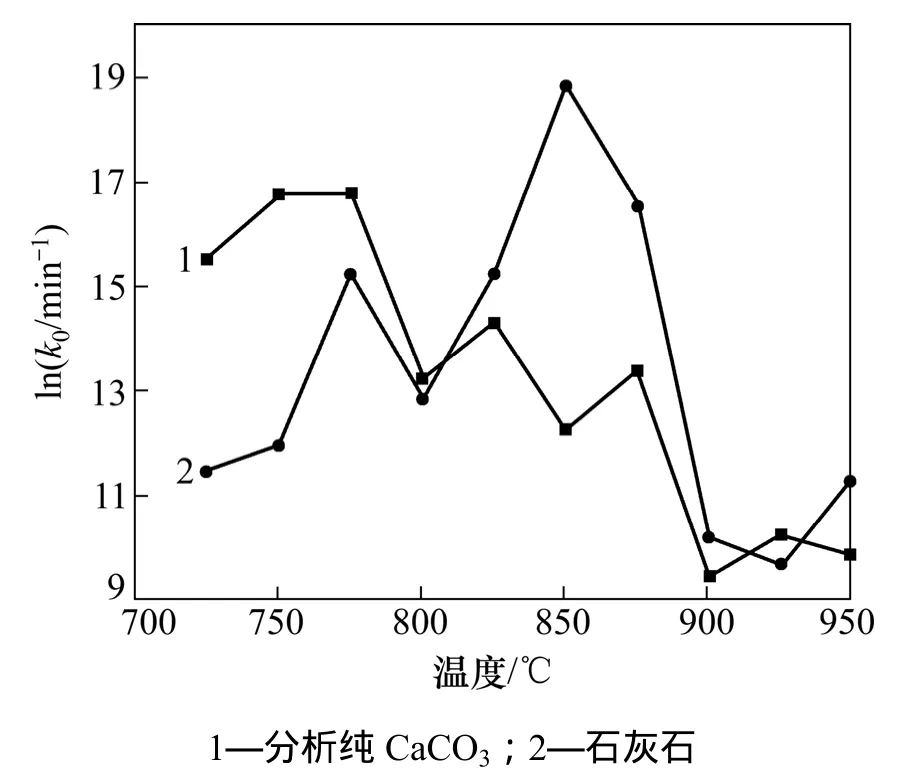
图5 温度对指前因子的影响Fig. 5 Effects of temperature on pre-exponential factor
图4和图5分别为不同温度下钙基吸收剂表观活化能E和指前因子k0的变化。由图4和5可知:分析纯 CaCO3和石灰石分解反应的动力学参数随温度变化并不一致。对于分析纯CaCO3煅烧反应,表观活化能E和指前因子k0随温度的增加总体上呈锯齿形减小的规律;而石灰石煅烧反应则变化不规律,大体上呈现先降后增再降的趋势。分析纯碳酸钙由于含有杂质较少,基本上为CaCO3粉末,因此随着温度的升高,动力学参数单调变化;而石灰石由于MgCO3,Al2O3,Fe2O3和K2O等杂质的存在,可能会在不同的温度阶段参与分解反应,最终导致动力学参数变化不规律。为了比较不同钙基吸收剂的分解动力学特性,对不同温度下的动力学参数求均值,分别得到分析纯CaCO3和石灰石分解反应的平均活化能为 143.17 kJ/mol 和143.52 kJ/mol,平均指前因子为 4.74×106min-1和1.74×107min-1。对比二者的动力学参数可知,平均活化能基本相同,石灰石分解反应的平均指前因子较大,说明石灰石分解反应中活化分子有效碰撞次数较多,石灰石分解反应较快。
2.5 补偿效应
由上分析可知:分析纯CaCO3和石灰石分解反应在700~975 ℃范围内的平均活化能基本相同,石灰石分解反应的平均指前因子较大,但在不同的温度范围,动力学参数的比较并不单一,大致可以分为3个阶段。在725~800 ℃温度范围内,分析纯CaCO3分解反应的表观活化能和指前因子较石灰石分解反应的大;800℃~900 ℃温度范围内,石灰石分解反应的表观活化能和指前因子较分析纯 CaCO3分解反应的大;900~950℃温度范围内,二者的表观活化能和指前因子基本相同。如果简单地将3个阶段的动力学参数进行比较,无法得出石灰石分解的反应性较分析纯CaCO3的大。但对比图4和图5可知:表观活化能和指前因子随温度变化规律趋于一致,即活化能增减的同时指前因子也随之增减。活化能增加使反应速率变慢,但指前因子增加又可使反应速率加快,即活化能与指前因子之间存在补偿效应。正是由于补偿效应的存在,不能简单地从表观活化能或指前因子来确定其反应性。
补偿效应通常可表示如下:
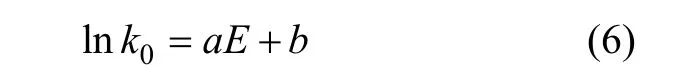
式中:a和b为补偿系数。对不同温度下的动力学参数进行线性拟合,拟合数据见表3,拟合直线见图6。由表3可知:线性拟合的相关系数接近1,说明ln k0与E之间存在良好的线性关系。

表3 补偿线拟合数据Table 3 Fitting data of compensation line
由图6可知:石灰石分解反应动力学参数间的补偿线比分析纯CaCO3的补偿线高。谢克昌[16]在研究不同煤种非催化气化和催化气化反应动力学参数间的补偿效应时,发现催化气化动力学参数间的补偿线比非催化气化的补偿线高,且不同催化剂下的催化气化动力学参数间的补偿线也不相同,催化效果越好,补偿线越高。由上分析可知:表征分解反应快慢的反应性指数和反应速率常数石灰石均较分析纯CaCO3大,石灰石的补偿线在分析纯CaCO3的补偿线的上部,因此可以得出补偿线的高低可以成为判断钙基吸收剂分解反应快慢的一个依据。
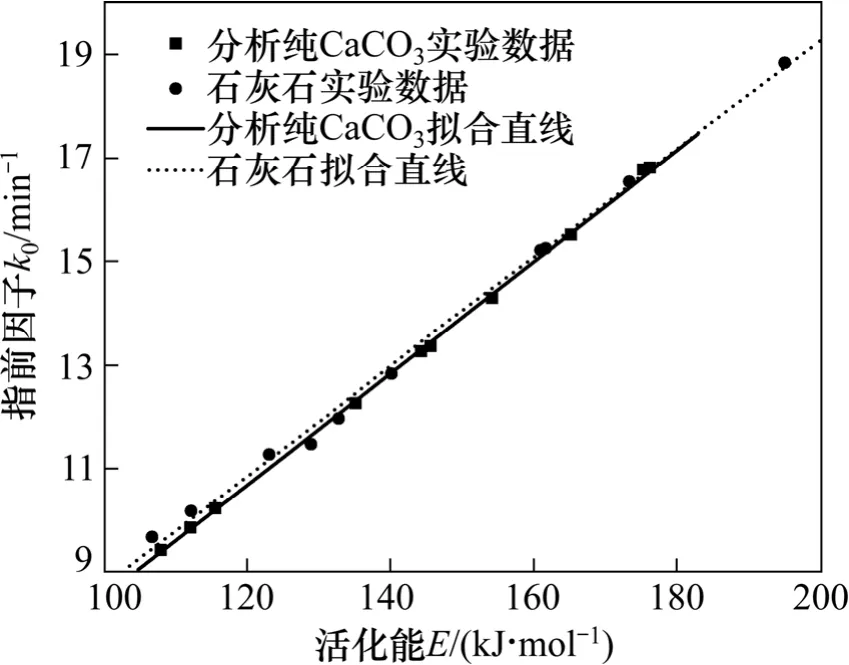
图6 活化能与指前因子的关系Fig. 6 Relationships between activation energy and pre-exponential factor
2.6 补偿效应的意义
近年来,对补偿效应有了多种探索性的理论解释。Sosnovski[17]认为可用2种具有不同活化能物质来解释补偿现象;Galwey等[8]则认为补偿现象可能与表面非均匀性相关;Krug[18]认为补偿现象是由实验误差及实验设备造成的;Curtis等[19]给出了一种广义的解释,他认为非均相反应动力学的过渡态理论较适合解释此现象。过渡状态理论认为化学反应并不是通过反应物分子的简单碰撞(有效碰撞理论)而完成的,而是反应首先形成一个不稳定的活化络合物(活化体)状态,在这个活化络合物状态下原子间的距离比正常化学键大,活化络合物的键比正常键弱,但其仍能向正常分子一样进行平动、转动和有限制的振动。动力学参数间的补偿效应在表面上是活化能和指前因子间的补偿效应,实际上可以归结为形成不稳定活化体的活化熵和活化焓的线性关系。实验结果清晰地显示不同温度下石灰石和分析纯 CaCO3分解反应的补偿线并不相同,这意味着石灰石和分析纯CaCO3分解过程中形成的不稳定活化体彼此并不相似,在结构上和稳定上存在差异。石灰石由于含有较多的杂质,在分解反应中会参与其中,而分析纯CaCO3杂质极少,因此会导致二者在分解反应中形成的不稳定活化体在结构上和稳定上存在差异,最终导致石灰石和分析纯CaCO3补偿线的不同。
3 结论
(1) 分析纯CaCO3和石灰石分解反应的动力学参数随温度变化而变化,但二者的变化规律并不相同。
(2) 当煅烧温度变化时,活化能和指前因子变化趋势相同,存在动力学补偿效应。
(3) 动力学参数间的补偿线可以成为判断不同钙基吸收剂分解快慢的一个依据。
[1] Abanades J C, Anthony E J, WAN G J, et al. Fluidized bed combustion systems integrating CO2capture with CaO[J].Environ Sci Technol, 2005, 39(8): 2861-2866.
[2] Salvador C, LU D, Anthony E J, et al. Enhancement of CaO for CO2capture in an FBC environment[J]. Chem Eng J, 2003,96(3): 187-195.
[3] Stanmore B R, Gilot P. Review calcinations and carbonation of limestone during thermal cycling for CO2sequestration[J]. Fuel Process Technol, 2005, 86(16): 1707-1743.
[4] 齐庆杰, 马云东, 刘建忠, 等. 碳酸钙热分解机制的热重试验研究[J]. 辽宁工程技术大学学报, 2002, 21(6): 689-692.QI Qingjie, MA Yundong, LIU Jianzhong, et al.Thermogravimetric experiment research on thermal decomposition mechanics of calcium carbonate[J]. Journal of Liaoning Technical University, 2002, 21(6): 689-692.
[5] 范浩杰, 章明川, 吴国新, 等. 碳酸钙热分解的机制研究[J].动力工程, 1998, 18(5): 40-43.FAN Haojie, ZHANG Mingchuan, WU Guoxin, et al. On the mechanism of high temperature dissociation of calcium carbonate[J]. Power Engineering, 1998, 18(5): 40-43.
[6] 仲兆平, Telfer M, 章名耀, 等. Caroline石灰石热分解实验研究[J]. 燃烧科学与技术, 2001, 7(2): 110-114.ZHONG Zhaoping, Telfer M, ZHANG Mingyao, et al.Experimental study on pyrolysis of caroline limestone[J]. Journal of Combustion Science and Technology, 2001, 7(2): 110-114.
[7] 徐秀峰, 崔洪, 顾永达, 等. 煤焦制备条件对其气化反应性的影响[J]. 燃料化学学报, 1996, 24(5): 404-410.XU Xiufeng, CUI Hong, GU Yongda, et al. Influence of charring conditions of coal chars on their gasification reactivity by air[J].Journal of Fuel Chemistry and Technology, 1996, 24(5):404-410.
[8] Galway A K, Brown M E. Compensation parameters in heterogeneous catalysis[J]. J Catal, 1979, 60(2): 335-338.
[9] Hashimoto K, Miura K, Watanabe T. Kinetics of thermal regeneration reaction of activated carbons used in waste water treatment[J]. AIChE J, 1982, 28(5): 737-746.
[10] 张雷, 田园, 路春美. 工业废弃物煅烧动力学的热重分析与研究[J]. 煤炭学报, 2011, 36(4): 681-687.ZHANG Lei, TIAN Yuan, LU Chunmei. Thermogravimetric analysis and study on calcination kinetics of industrial wastes[J].Journal of China Coal Society, 2011, 36(4): 681-687.
[11] 冯仰捷, 陈炜, 邹文樵. 固体热分解动力学机制的研究[J]. 华东化工学院学报, 1991, 17(5): 591-599.FENG Yangjie, CHEN Wei, ZOU Wenqiao. Kinetic mechanism of solid thermal decomposition with non-isothermal gravimetric analysis[J]. Journal of East China Institute of Chemical Technology, 1991, 17(5): 591-599.
[12] 李梅, 张洪. 石灰石分解特性的热重法研究[J]. 煤炭转化,2006, 29(4): 26-28.LI Mei, ZHANG Hong. Thermal analysis on the decomposing characteristics of limestone[J]. Coal Conversion, 2006, 29(4):26-28.
[13] 胡荣祖, 史启祯. 热分析动力学[M]. 北京: 科学出版社, 2001:127-131.HU Rongzu, SHI Qizhen. Thermal analysis kinetics[M]. Beijing:Science Press, 2001: 127-131.
[14] 王世杰, 陆继东, 胡芝娟, 等. 水泥生料分解动力学的研究[J].硅酸盐学报, 2003, 31(8): 811-814.WANG Shijie, LU Jidong, HU Zhijuan, et al. Study on kinetics of decomposition of cement raw meal[J]. Journal of the Chinese Ceramic Society, 2003, 31(8): 811-814.
[15] 张保生, 刘建忠, 周俊虎, 等. 基于无模式法推断石灰石分解机理新方法[J]. 化工学报, 2007, 58(5): 1204-1210.ZHANG Baosheng, LIU Jianzhong, ZHOU Junhu, et al. New model-free method based approach to mechanism of limestone decomposition[J]. Journal of Chemical Industry and Engineering,2007, 58(5): 1204-1210.
[16] 谢克昌. 煤的结构与反应性[M]. 北京: 科学出版社, 2002:343-350.XIE Kechang. Coal structure and its reactivity[M]. Beijing:Science Press, 2002: 343-350.
[17] Sosnovski H H. The catalytic activity of silver crystals of various orientations after bombardment with positive ions[J]. Phys Chem Solids, 1959, 10(4): 304-310.
[18] Krug R R. Detection of the compensation effect (θ rule)[J]. Ind Eng Chem Fundam, 1980, 19(1): 50-59.
[19] Curtis W M, Conner J R. A general explanation for the compensation effect: The relationship between ΔS and activation energy[J]. J Catal, 1982, 78(1): 238-246.
