区域公交的多车场车辆调度优化

徐瑜婷，宋 瑞，郑 锂

（北京交通大学交通运输学院，北京 100044）

区域公交的多车场车辆调度优化

徐瑜婷，宋 瑞，郑 锂

（北京交通大学交通运输学院，北京 100044）

在运营企业费用最少的基本模型基础上，以乘客等待费用最少为目标函数讨论多车场车辆调度问题，并建立相应模型。基于逆差函数算法对模型求解，设计两种方法进行求解:一种是人工插入空驶车程，求解过程中加入乘客等待时间的限制;另一种是通过由逆差函数为基础设计的PT-Manager仿真软件进行算法优化，对实际案例进行参数标定以及求解。结果表明:该模型逆差函数算法求解过程简单、结果直观，PT-Manager仿真软件能够帮助公交调度人员进行车辆调度及优化，对现有的车辆调度以及多车场的发展有一定的指导意义。

多车场调度;逆差函数;车辆调度;PT-Manager

0 引言

解决现代城市交通拥堵问题的最主要方法之一是大力发展城市公共交通，而运营调度规划是公共交通的主要难点之一。而公共交通规划的运营调度分为客流需求预测、时刻表的编制、行车计划、人员的配置等4个方面，由此可见，公交车辆调度是公交规划及运营管理中非常重要的环节。

公交车辆调度主要分为多车场车辆调度（Multiple Deport Vehicle Scheduling Problem，简称MDVSP）和单车场车辆调度。其中，单车场的车辆只能在固定的车场间运行，多车场调度车辆可以在多个车场间被调用，并允许车辆分布于多个车场。单车场车辆调度具有简单、便于管理的优点，多车场车辆调度则更有利于运输资源的合理和优化调度，更符合社会可持续发展的要求。多车场车辆调度以一个区域内的车场整体为研究对象，公交运营组织和调度的区域大可包含整个城市的公交运营线路，小可只包含2～3条单线模式的运营线路，具体的每一个区域大小的确定主要是以整个区域的运营效率为最高这个标准来确定的。研究表明，通过对区域内公交车辆的统一管理，可以大大提高车辆利用率，降低运营成本［1］。我国现有的车辆调度多为单车场调度问题，车场对车辆的规划管理以每个车场为目标，为提高公交运营效率减少道路拥堵程度，笔者以区域公交车辆调度为研究对象，探讨适合我国实际情况的区域公交调度。

国内外研究学者对多车场调度问题进行了大量研究，Ceder，等［2-3］以公交网络中两辆公交车相遇的次数最大及乘客等待时间最少为目标，对公交区域同步换乘进行了研究。在此基础上，A.Haghani，等［4］引入站点换乘权重与线路换乘吸引度，以乘客总换乘等待时间最少为目标建立了公交区域调度模型。此后，D.Huisman，等［5］提出了用插入最小空驶车程的逆差函数的方法来分析车辆的调度问题。邹迎［6］在对北京公交区域运营组织与调度系统初步探讨中，提出了多线路车场调度问题。石琴，等［7］提出了基于换乘优化的公交区域调度模型。此外，张欣伟，等［8］研究了在提供公共交通信息条件下公交换乘时间最短的调度问题，并提出了线性规划模型。

车辆调度求解算法以智能算法居多。采用遗传算法、禁忌搜索算法、蚁群算法等智能搜索算法解决车辆调度问题，能覆盖大区域的车辆调度问题，通常能计算3个及以上车场数量的区域车辆调度问题，最终的最优解通过计算机大规模计算得出，质量较高且更符合实际情况。但就中国实际情况考虑，基于逆差函数算法的仿真软件能得出简单易懂的阶跃函数，能计算出各车场各个时刻的车辆数。在插入空驶车程，即当运营中插入扰动情况时，智能算法经过复杂冗长计算才能得出结果，而逆差函数只需调度人员对图形进行插入，操作简单，出错率低。

笔者旨在建立以企业花费最少、以乘客在各车场的等待时间最短以及等待费用最少的目标函数。在算法的运用中，首先运用遗传算法、禁忌搜素、模拟退火等智能算法［9］得到初始解，然后采用逆差函数插入空驶车程减少车队规模进行解的优化调整。这一过程中逆差函数算法搜索收敛性以及求解的优质性劣于直接采用智能算法得出最优解，但是以模拟仿真为基础的逆差函数便于实际仿真，能对实际情况优化仿真，算法得出的结果易于处理，每插入空驶车程，都能对结果进行动态输出，简单易懂，易于操作和理解。

1 问题描述与建模

1.1 问题描述

公交时刻表提供了各公交班次信息，包括出发时间和到达时间等，如图1。图中，班次i的出发时间为Si，到达时间为ei，班次i结束时刻到班次j开始时刻之间的运行时间为ti，j。目标车辆在完成班次i后可继续进行班次j的必要条件为:ei+ti，j≤sj。如果车辆执行上述的班次，则连接两者之间的班次常常称为空驶班次，此时的班次为不载乘客班次。安排空驶班次的目的是减少整个车队的规模。反之，如果班次j的到达时刻加上i至j班次间的运行时间小于班次i的出发时刻，则可以用班次j的车辆继续完成班次i。

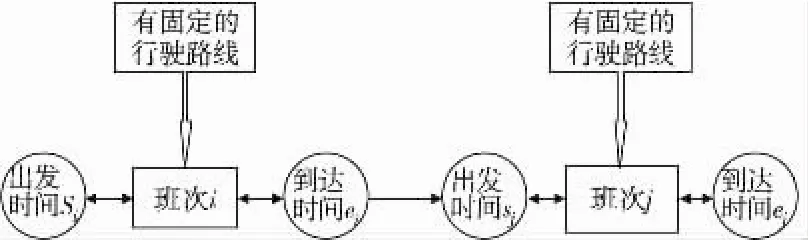
图1 插入空驶车程示意Fig.1 Insert deadheading trips diagram

每辆车可以连续完成一系列的班次，形成车次链（图2）。定义车辆从该车场驶出的第1班次为出场班次，与之相对应，当车辆执行完相应的调度任务，回归车场所完成的最后一次运输称为入场班次。一辆车的车次链包含出场班次、入场班次和一系列的空驶车次以及常规班次。而这些班次的对应费用称为出场费用、入场费用，以及空驶费用。

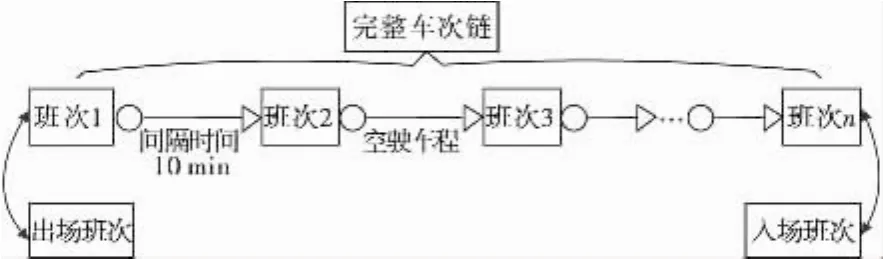
图2 车次链形成Fig.2 Train chain diagram

在已知行车时刻表的基础上，可用逆差函数求解多车场车辆调度问题。逆差函数是一个阶跃函数，用以表示的是每个车场当前的车辆数，当车辆从车场出发执行一个班次时，阶跃函数的函数值增加1，当车辆回到车场时，其函数值减少1。把所有车场的函数值相加，得到总的阶跃函数，即为该研究对象区域所需要的车队规模的大小。在每个车场的阶跃函数的构建过程中，需要对应线路的时刻表数据，以横轴表示时刻表的时间，纵轴表示车辆数量。某线路某时刻由车场出发的总班次数与总到达班次数之差见式（1）:

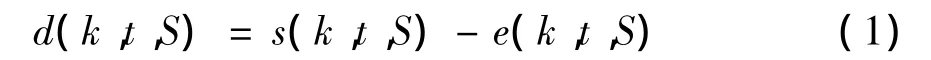
式中:k为车场编号，k=1，2，3，…，K（K表示研究区域内的车场总数）;t代表研究时刻;S代表研究时段内对应时刻表中所有班次的集合;d（k，t，S）表示从开始时刻到t时刻的车场k出发总班次数与总到达班次数之差;s（k，t，S）表示所有班次集合S中从开始时刻到t时刻之间的车场k到达的车辆总和;e（k，t，S）表示t时内研究的所有的班次集合S中从开始时刻到t时刻之间的车场k内到达的车辆总和。

设D（k，S）为研究时段t内车场k的总班次之差d（k，t，S）的最大值，如式（2）:

多个车场的逆差函数值之和就是总的车辆数，设全局逆差函数（即t时内的所有车场逆差函数之和）为g（t，S）。g（t，S）在t时内的最大值用G（t，s）表示。插入空驶班次的条件为:当研究区域达到最大值G（S）的时刻为t*，在t*之前执行一个空驶班次DH1。如果这趟空驶班次在时刻由车场u发出，在时刻到达车场v，那么必须满足条件。当完成空驶车次的插入后，时刻表对应的车次时间变为S1=S+DH1。如果在sv1时刻，车场v达到其容量极值区间，则存在t*之前或是恰在t*达到极值区间的情况有［10］:

只有式（5）的情况是唯一可能减少需用车辆数量的情况。所以在车场v到达极值区间的时刻之前可在车场u，v之间插入第一个空驶车程，形成第一个空驶班次DH1。

在插入空驶班次DH1以后，为避免车场u在到达极值区间的时候车辆数量不够的情况发生，也为了减少车队规模，在车场u极值区间之前插入新的空驶班次以消除车场u的需用车辆数的变化。设定执行这次空驶的班次为DH2，自车场q出发到达车场u，这里的车场q可以是车场v，也可以是其他车场，发车的到达区间为［，］，其中，。

1.2 模型建立

区域公交车辆调度模型的目标函数多是企业花费费用最少。实际上，除了考虑企业的运营效益外，还要考虑乘客的满意度。笔者加入乘客等待时间费用来体现对乘客满意度的考虑。

模型具体形式如下:

式中:cq∈［x，y］，q∈w;x，y为任意值，且满足x＞y;av，p表示路径p是否包含点v∈B，若包含，则av，p=1，反之av，p=0;yp表示与每条路径相关联的0-1变量，若有车次通过p，则yp=1，反之yp=0;cp表示包含弧的费用;Ωk表示车站场k出发，经历集合B中一些节点后返回相同车场的路径集合;cq表示车场k的乘客q单位等待费用;q表示在车场k等车的乘客;W表示各个车场等车乘客总体集合;dk表示车场k的车辆数容量;∂q表示车场k的乘客等待的权重。

式（7）为目标函数，其中，cpyp表示企业的花费费用，cqyp∂q表示乘客的等待费用。约束条件中，式（8）保证每个班次j∈B只能由某一车场的1辆车完成;式（9）表示车场车辆数不超过车场的容量;式（10）限制车辆在路径上运行与否，取值只能是“0”或“1”;式（11）限制所有乘客在各车场的等待权重之和为1。

2 求解算法

2.1 求解过程基本介绍

逆差函数算法是通过PT-Manager软件来实现的。首先采用文献［10］中的方法实行邻域搜索得出初始解，然后用逆差函数算法对初始解进行优化，采用仿真软件进行仿真分析，在模型约束中加入乘客等待时间的容忍度进行算法计算得出最终解。

2.2 逆差函数算法

逆差函数算法是采用图形方法求解每个车场实时的车辆情况。通过插入空驶车程来减少整个研究区域的车队规模，得到车队规模下限。

用逆差函数求解多车场问题步骤如下:

1）根据固定行车计划下确定的时刻表，得出任意车次的出发车场u、到达车场v以及两车场之间的运行时间t，分别得出任意车场k的逆差函数图d（k，t，S）。

2）比较各车场的逆差函数图，选择容量极值区间最长的车场a为研究对象。

3）选择最先有车到达即最先到达最大值的车场b，若该时刻车场b到达车场a的空驶时间大于车场a下一班次的发车时间，则插入空驶车程1，反之依次查看各车场是否能插入空驶车程到车场a。

4）重复上述第2）步直到a车场无法再插入空驶车程减少车队规模为止。

5）若剩余各车场由于插入空驶车程到a，使得自车场的车队规模增加，则选择从别的车场间插入空驶车程保证该车场车队规模不变，依次调整直到除了a车场以外其余车场车队规模不变。

6）依次检验所有车场是否能插入空驶车程，直到所有车场检查完成后，转到第7）步，否则转到第3）步。

7）算法结束，得到插入空驶车程的解。

2.3 PT-Manager仿真软件求解

在PT-Manager仿真软件上执行上述逆差函数算法。PT-Manager仿真软件是由Altdoit Software Solutions公司开发运行的仿真软件，针对逆差函数求解多车场车辆调度问题进行仿真。通过直接输入相关时刻表、车次信息得出各车场逆差函数d（k，t，S）以及全局逆差函数g（t，S），进一步通过空驶信息输入，得出空驶车次。具体步骤为:

1）根据时刻表输入每个车次的运行信息，包含车次名称、出发车场、到达车场、出发到达时间等。

2）确认输入所有车次信息后，运行程序，得出各个车场的逆差函数图形。

3）选择空驶车程的输入。有两种方式可供选择，第1种方式是直接得出各车场间的空驶时间及空驶里程，输入到软件的空驶矩阵中，自动生成空驶车次，转到第3）步;第2种方式是依据各车场的逆差函数手动输入每一空驶车程车次名称，出发车场、到达车场、两车场间空驶时间，不断调整，保证每个乘客在每个车场等待时间不超过模型建立中约束条件（11）以及乘客能容忍的在车场之间的等待时间的要求，直到不能再减少车队规模时，转到第5）步。

4）得到空驶矩阵进行运行，输入乘客能容忍的最长等待时间，运行得出空驶车次。

5）依据得出的空驶车次进一步修改时刻表，优化时刻表，减少整个研究范围的车队规模。

6）输出插入的空驶车程和时刻表变化的情况，得出插入空驶车程前后的时刻表，比较优化结果。

7）由实际情况得出各车场乘客等待权重，计算插入空驶车程前后的目标函数值，比较分析空驶车程插入的合理与否。

3 案例分析

选取北京市公交线路l1，l2，l3，l4，分别代表 320路、309路、运通105路和103路，进行多车场车辆调度的实例分析。这4条线包含3个车场A、B和C，公交线和车场布置如图3。

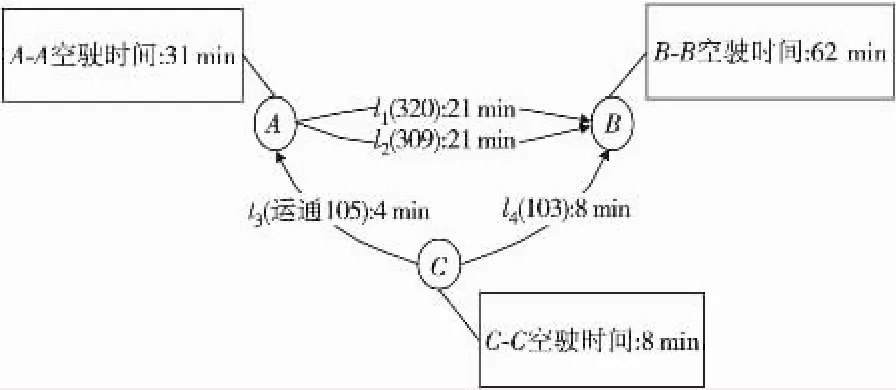
图3 区域车场间的位置信息及其线路信息Fig.3 Position and road information about multiple depot diagram

3.1 参数设置及数据输入

设定线路的单位运行费用c320=3，c65=6，c运通105=4;在仿真软件中，取各车场乘客的等待权重αq值相同，分别为αA=αB=αC=1/3;以及取值αA=0.25，αB=0.3，αC=0.45，同时cq=5，求解过程如图4。图4（a）代表A车场插入空驶车程前车场逆差函数;当1.2节模型中目标函数的y取值为10 min时，运行得出的空驶车次见图4（b）。

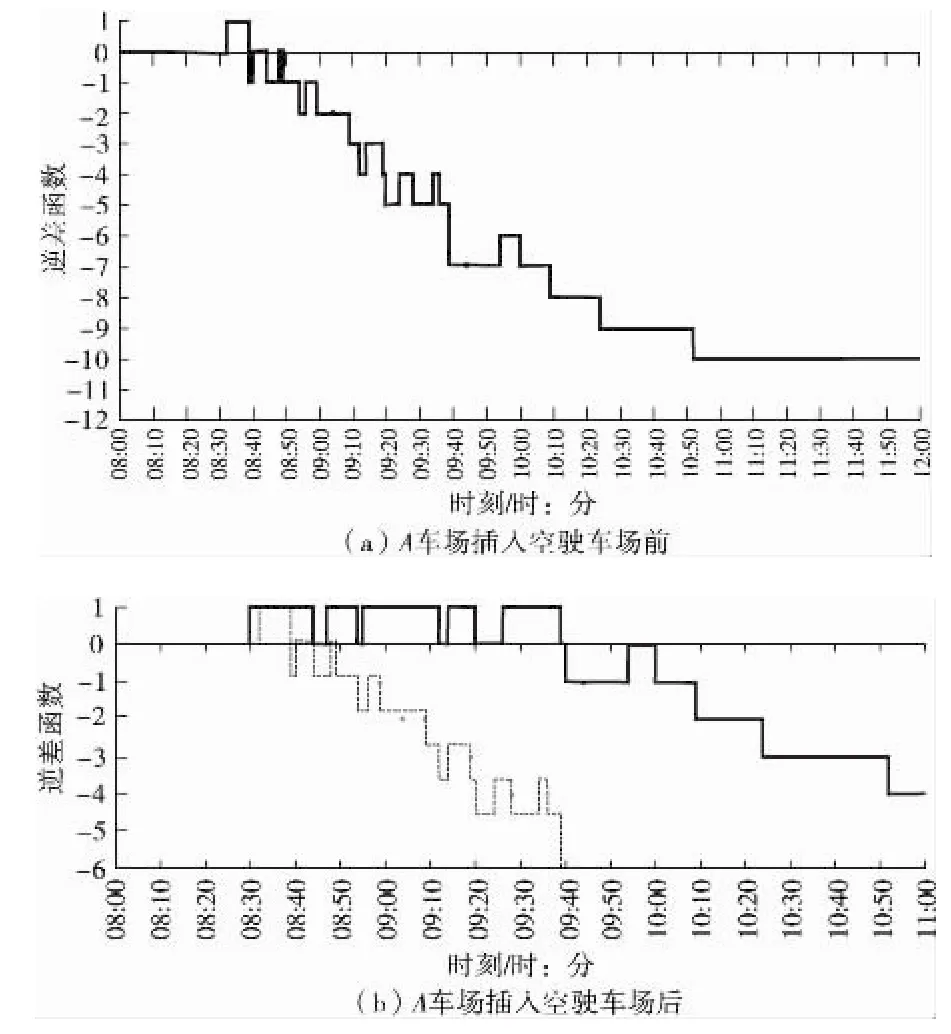
图4 A车场插入空驶车场前后逆差函数Fig.4 A depot’s DF before/after insert deadheading diagram

3.2 优化结果分析

经过求解得到插入空驶车程如表1。

表1 研究区域插入空驶车程的车次Table 1 Timetable after insert deadheading trips

在插入的空驶车程和时刻表变化的情况，得出插入空驶车程前后的时刻表，如表2。将参数值代入目标函数（7）中，取3车场等待权重相同得出，插入空驶车程前目标函数值为96.00;插入空驶车程后目标函数为 59.33。而取值 αA=0.25，αB=0.3，αC=0.45，得出插入前后的目标函数值分别为104.32及76.48。

表2 研究区域各车场优化前后车队规模Table 2 Vehicle quantity before and after inserting deadheading trips

从不同车场的取值权重可以看出，虽然目标函数值变大，但是对于每个车场来说，对乘客的重要程度有一定改变，更符合实际情况，能充分考虑每个车场的乘客等待满意程度。由于乘客的等待费用的不同可能会导致不同车场的乘客要求不同，而造成不同车场权重的不同。

从相同取值权重的车场插入空驶车程前后可以看出，在原有的时刻表（固定行车计划）的基础上，得出的各个车场逆差函数，在PT-Manager仿真软件中，分别输入各车次的运行状态，加入乘客的等待时间的函数后，求出插入的空驶车程，发现车队规模由原来的18辆减少为11辆，同时目标函数降低38.2%。把上述插入空驶车程的结果带回时刻表，可对时刻表进行调整优化。

4 结语

以运营企业成本费用和乘客等待费用之和最小为目标函数，建立了多车场车辆调度模型。利用人工和PT-Manager仿真软件求解，详细给出了求解步骤。结合北京实际运营进行算例分析，采用PTManager仿真软件求解，考虑不同车场乘客等待权重不同即乘客的满意程度不同，结果得到研究区域整体的车队规模减少了7辆，降低企业的运营成本，同时乘客在每个车场的等待时间不超过10 min，提高乘客满意度，使得各车场之间车辆衔接更合理，证明了模型合理性。

（References）:

［1］ 刘志刚，申金升，杨威.基于禁忌搜索的公交区域调度配车模型研究［J］.交通运输工程与信息学报，2007，5（4）:63-67.

Liu Zhigang，Shen Jinsheng，Yang Wei.Study on multiple bus vehicle dispatching based on Taboo research［J］.Transportation Engineering and Information Technology，2007，5（4）:63-67.

［2］ Ceder A.Methods for creating bus timetables［J］.Transportation Rearch:Part A，1986，21（1）:59-83.

［3］ Ceder A，Golany B，Tal O.Creating bus time tables with maximal synchronization［J］.Transportation Research:Part A，2001，35（10）:913-928.

［4］ Haghani A，Banihashemi M，Chiang K H.A comparative analysis of bus transit vehicle scheduling models［J］.Transportation Research:Part B，2003，37（4）:301-322.

［5］ Huisman D，Freling R，Albert P M，et al.A robust solution approach to the dynamic vehicle scheduling problem［J］.Transportation Science，2004，38（4）:447-458.

［6］ 邹迎.公交区域调度行车计划编制方法研究［J］.交通运输系统工程与信息，2007，7（3）:78-82.

Zou Ying.Study on bus regional scheduling travel plan organizing method［J］.Journal of Transportation Systems Engineering and Information Technology，2007，7（3）:78-82.

［7］ 石琴，覃运梅，黄志鹏.公交区域调度的最大同步换乘模型［J］.中国公路学报，2007，20（6）:90-94.

Shi Qin，Qin Yunmei，Huang Zhipeng.Maximal synchronous transfer model of bus regional dispatching［J］.China Journal of Highway and Transport，2007，20（6）:90-94.

［8］ 张欣伟，张贵兰.城市公交线网规划体系研究［J］.交通企业管理，2008，12（5）:62-64

Zhang Xinwei，Zhang Guilan.Study on urban bus routes planning system［J］.Transportation Enterprise Management，2008，12（5）:62-64.

［9］ Zhang Qiao，Xu Xu，Liang Yanchun.An improved artificial immune algorithm with a dynamic threshold［J］.Journal of Bionic Engineering，2006，3（2）:92-97.

［10］赛德尔，关伟.公共交通规划与运营理论、建模及应用［M］.北京:清华大学出版社，2010.

Ceder A，Guan Wei.Public Transport Planning and Operation of the Theory，Modeling and Application［M］.Beijing:Tsinghua University Press，2010.

Optimization of Vehicles Dispatching Model for Multiple Depots in Regional Traffic

Xu Yuting，Song Rui，Zheng Li
（School of Traffic＆ Transportation，Beijing Jiaotong University，Beijing 100044，China）

On the base of the fundamental model whose objective was to minimize the company’s costs，multiple depot dispatching problem was discussed and then the corresponding model was established，in which minimizing passengers’waiting expense was considered in the objective function.Then deficit function was used to solve the objective function，which can be solved in two different ways:firstly，manual work was used to insert the deadheading trips to restrict the passengers’waiting time;secondly，PT-manager simulation software which was built on the base of deficit function was introduced to simulate and analyze.In order to make a statistic explore the actual data was introduced.The results proved that the using deficit function to solve the proposed model is simple and accurate.PT-manager simulation software could provide guide and optimization for bus dispatching staff，which also could provide referential significance to the current bus dispatching and the development of multiple depot dispatching.

multiple depot dispatching;deficit function;vehicle dispatching;PT-Manager

U280

A

1674-0696（2013）02-0258-05

10.3969/j.issn.1674-0696.2013.02.19

2012-05-31;

2012-09-21

中央高校基本科研业务费专项基金项目（2009YJS044）

徐瑜婷（1988—），女，重庆忠县人，硕士研究生，主要从事城市交通规划与管理方面的研究。E-mail:11121015@bjtu.edu.cn。