自锚式斜拉桥的极限跨径研究(I)
2013-06-02张杨永
张杨永
(上海同豪土木工程咨询有限公司,上海 200092)
自锚式斜拉桥的极限跨径研究(I)
张杨永
(上海同豪土木工程咨询有限公司,上海 200092)
从斜拉索和主梁的材料强度入手探讨了当前材料水平和施工水平下全自锚斜拉桥结构体系的极限跨径。研究结果表明:横向静阵风作用下的主梁强度是限制斜拉桥跨径增大的主要因素,活载作用下的主梁强度居于次要地位,而斜拉索的强度和效率对斜拉桥极限跨径的影响最小;斜拉桥极限跨径突破的首要问题是提高主梁的侧向刚度。研究成果可供超大跨度斜拉桥概念设计时参考。
斜拉桥;极限跨径;极限静阵风;垂度效应;侧向刚度
自20世纪70年代开始,国内外的许多学者[1-10]就超大跨度斜拉桥的极限跨径与力学性能等开展了一系列技术论证和探索。丹麦的Gimsing[2]从斜拉索使用效率比出发,推算出斜拉桥的最大跨径可达到5 000 m;中国的李国豪[3]从斜拉索弹性模量非线性影响出发提出最大跨径可达3 600 m;瑞士的 U.Meier[4]认为钢桥的极限跨度为 5 000 ~7 000 m,采用新型碳纤维加劲复合材料,其极限跨度可达15 000 m;法国的 J.M.Muller[5]认为采用“双锚拉索体系”可以有把握地做到3 000 m;德国的 R.Saul[6]对2 000 m左右的斜拉桥和悬索桥作了全面的分析比较,认为斜拉桥在经济上更胜一筹。
目前,已建的超大跨度斜拉桥均采用常规双塔3跨全自锚结构体系,空间倾斜双索面布置。在当前的材料发展水平和施工技术水平下,研究这种结构体系的极限跨径,无疑具有一定的现实意义。王伯惠[9-10]曾对斜拉桥的极限跨径作了较为系统的研究,但未考虑拉索垂度、静阵风作用、主梁屈曲稳定性等因素的影响,而静阵风作用往往是超千米级斜拉桥的控制工况。在此基础上,结合近似计算公式[1],笔者从斜拉索和主梁的材料强度方面对常规体系斜拉桥极限跨径作进一步的探讨。
1 斜拉索的强度
斜拉桥受力最不利的斜拉索当属离索塔最远、靠近跨中的那根最长的拉索。随着斜拉桥跨径的增大,拉索的长度也逐渐增大,主跨1 088 m的苏通大桥最长的拉索达577 m,而主跨1 600 m斜拉桥方案的最长斜拉索已经达到851 m,超长斜拉索自重垂度很大,竖向支承效率变得很低,必须施加更大的索力才能拉紧。笔者分别就不考虑垂度效应和考虑垂度效应两个方面,讨论超长斜拉索的强度问题。对于超大跨度斜拉桥必须考虑拉索的垂度效应,这是毋庸置疑的。本文讨论不考虑垂度效应时斜拉桥极限跨径,目的在于与考虑垂度效应时的极限跨径情况作对比分析。
1.1 不考虑垂度效应(图1)
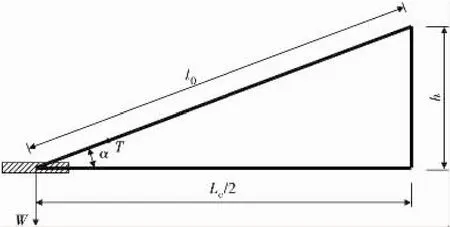
图1 斜拉索受力示意(不考虑垂度)Fig.1 Force diagram of stayed cable(sag ignored)
不考虑拉索自重引起的垂度效应时,可将拉索当作一根刚性直杆考虑。假设每根拉索只承担一个索距主梁节段的恒载、活载,并承担拉索自重的1/2,则有:
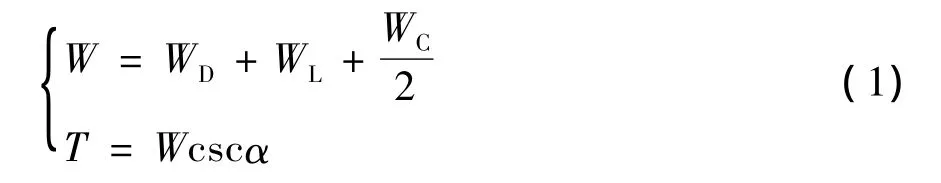
根据图1,可得:
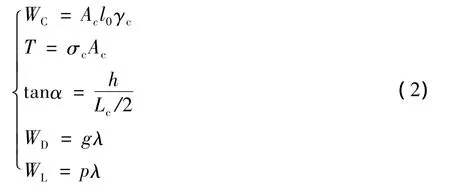
式中:W为斜拉索所要承担的竖向力;WD,WL,WC分别为主梁节段的恒载、活载以及斜拉索的自重;h为斜拉桥的索塔有效高度;Lc为主跨跨径;α为斜拉索的倾角;l0为斜拉索的切线长度;T为斜拉索的梁端索力;Ac,γc分别为斜拉索的截面面积和比重;g,p分别为主梁的恒载集度和活载集度;λ为中跨主梁的索距。
令斜拉桥的索塔有效高跨比h/Lc=e,则联解公式(1)、公式(2)可以得到斜拉桥跨径与拉索强度、索塔高跨比之间的关系式:

根据文献[1]的研究结论,对于超千米级斜拉桥,索塔高跨比e一般取值在0.19~0.26之间,跨径增大时,宜取较小值。随着跨径的增大,跨中主梁的节段长度(索距λ)逐渐缩短,笔者分析时考虑3种取值情况:10,15,20 m。
超长斜拉索宜采用高强平行钢丝或者钢绞线,目前使用的最大钢丝极限强度为1 770 MPa,安全系数取用2.5,则容许应力为708 MPa。按文献[3],单根拉索面积可以做到180 cm2,一般采用双索面布置。考虑索套等影响后,拉索的比重取用8.32×104N/m3。
对于恒载集度g的取值,昂船洲大桥2.62×105N/m,苏通大桥2.02×105N/m,考虑跨径增大等因素,文中取用3.0×105N/m。超千米级斜拉桥多采用6车道或者8车道布置,可根据有关规范[4]计算活载集度p。按8车道布置时,车道荷载横向折减系数为 0.50,纵向折减系数为 0.93,偏载系数取1.15,则活载集度取为 1.15×8 ×0.5×0.93×10.5=44.92×103(N/m),考虑到重车作用(即车道荷载中的集中力),活载集度乘以放大系数1.5,则活载集度为1.5×44.92×103=67.38×103(N/m)。因此,在计算中活载集度取用7×104N/m。
不同恒载集度和索距布置时,极限跨径与索塔高跨比之间的关系如图2。从图2中可以看出:极限跨径随着梁上拉索索距的减小而增大;随着主梁自重的降低而增大;随着高跨比的增大而增大。当梁上索距为10 m、主梁恒载集度取30 t/m、索塔高跨比取0.20时,斜拉桥的极限跨径为7 149 m;当恒载集度增加到40 t/m时,极限跨径降低到5 909 m。

图2 极限跨径与索塔高跨比之间的关系(不考虑垂度效应)Fig.2 Relationship of limitation span and ratio of tower height to span(sag ignored)
随着跨径的不断增大,斜拉索长度迅速增加,其重量也逐渐增大,按前面的假设,索力主要承担主梁恒载、活载以及拉索自重的1/2。显然,随着跨径的增大,斜拉索索力中用来承担自身重量的比例越来越高,而用来承担主梁恒载、活载的比例则越来越小。这里定义一个新的变量,用来表示斜拉索用来承担外荷载的那部分索力在总的索力中的比重,称之为斜拉索的有效承载系数:
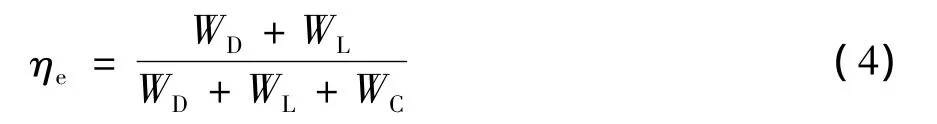
式中:ηe为斜拉索的有效承载系数。
经过简单转化可得:
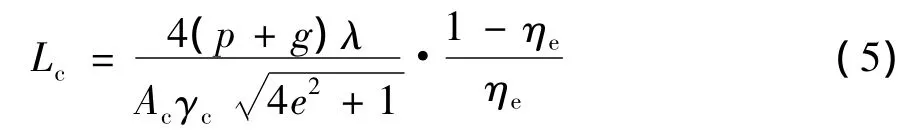
当主梁恒载集度取30 t/m,斜拉索有效承载系数与斜拉桥主跨跨径之间的关系如图3。从图3中可以看出,索塔高跨比对ηe影响较小,而索距对ηe影响较大。对于图3中的第1种情况,即梁上索距λ=10 m,索塔高跨比e=0.20,当主跨跨径4 500 m时,拉索自重就耗去承载能力的50%,而主跨跨径为10 000 m时,有效承载系数仅为30%。
1.2 考虑垂度效应
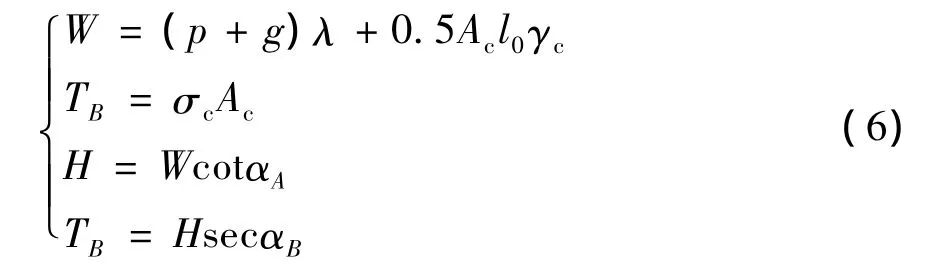
式中:TA,TB分别为斜拉索梁端和塔端的索力;H为斜拉索梁端索力的水平分量;αA,αB分别为斜拉索梁端和塔端的水平倾角,可按文献[1]推导的近似公式计算。
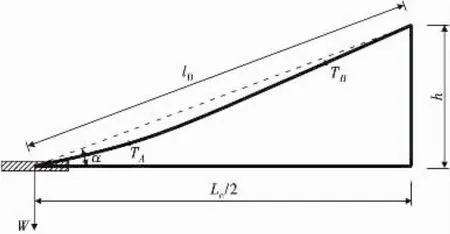
图4 斜拉索受力示意(考虑垂度)Fig.4 Force diagram of stayed cable(sag considered)
根据式(6)可以求出斜拉桥极限跨径与拉索强度、索塔高跨比之间的关系式为:

考虑拉索的垂度效应后,不同恒载集度和索距布置时,极限跨径与索塔高跨比之间的关系如图5。

图5 极限跨径与索塔高跨比之间的关系(考虑垂度效应)Fig.5 Relationship of limitation span and ratio of tower height to span(sag considered)
从图5可以看出:极限跨径随着梁上拉索索距的减小而增大;随着主梁自重的降低而增大;随着高跨比的增大而增大。当梁上索距为10 m,主梁恒载集度取30 t/m,索塔高跨比取0.20时,斜拉桥的极限跨径为3 057 m;当恒载集度增加到40 t/m时,极限跨径降低到2 539 m。由此可见,考虑拉索垂度效应后,斜拉桥极限跨径降低了1/2以上。在斜拉桥极限跨径研究中,必须考虑拉索的垂度效应问题。
由于拉索垂度引起的索长变化不是很大,所以,当考虑垂度效应时,斜拉索的有效承载系数与不考虑垂度效应时的情况基本相同。但由于垂度的影响,随着拉索长度的增加,梁端拉索的水平倾角降低,支承效率降低。对于有垂度的拉索,定义其竖向支承效率为:

式中:ηev为斜拉索的竖向支承效率;V0,V1分别为考虑垂度效应前后的斜拉索梁端索力的竖向分量。
由图5得:

拉索的竖向支承效率与主跨跨径之间的关系如图6。
夏国忠看出了战士们的情绪,趁吃饭的时间,他把战士们召集到起来训话:“兄弟们,我知道你们很苦很累,但我们更应当知道鬼子很凶很恶。总司令常对我们说,平时多流汗,打起仗来才能少流血。弟兄们,阵地不能丢,命也不能丢!你们说对不对?”
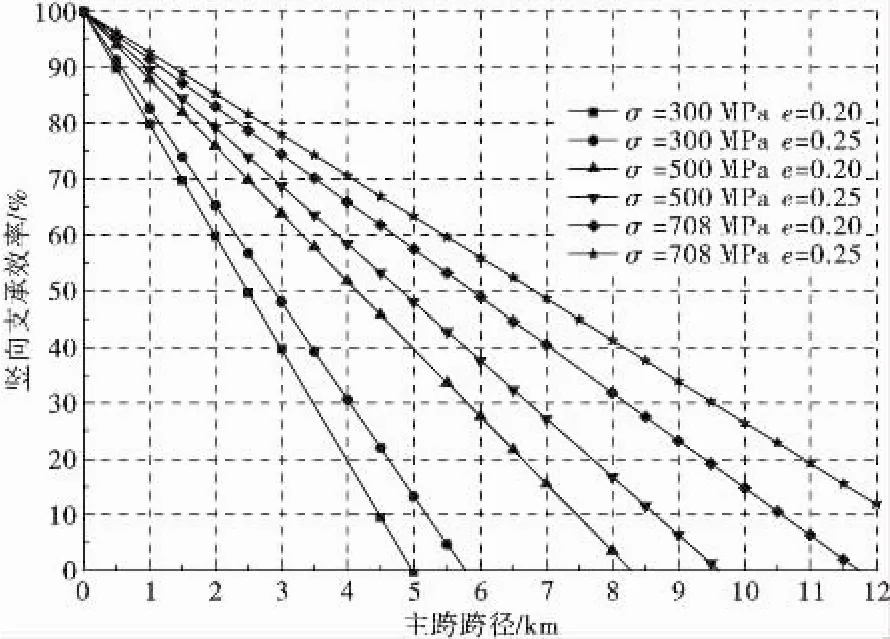
图6 拉索竖向支承效率与主跨跨径之间的关系Fig.6 Relationship of cable vertical bearing efficiency and main span
从图6中可以看出:随着跨径的增大,拉索的竖向支承效率迅速降低;当跨径一定时,拉索竖向支承效率随着拉索的应力水平和索塔的高跨比的增大而增大。当索塔高跨比取0.2时,如果要求拉索的支承效率不小于 50%,则拉索容许应力 300,500,708 MPa对应的最大跨径分别为 2 485,4 140,5 870 m。
影响斜拉索强度的主要因素有索塔高跨比、主跨跨径、主梁恒载集度、梁上索距、拉索容重等。当斜拉索的极限抗拉强度一定时,通过增大高跨比、减轻主梁自重、减小梁上索距等措施,可以有效地提高斜拉桥的极限跨径;采用轻质高强的FRP等新材料制成的拉索,则是提高斜拉桥极限跨径的另一种措施。
2 主梁的强度
从分析可知,主梁应力的最不利工况主要有恒载与活载作用组合及恒载与横向极限静阵风作用组合。
2.1 恒载 +活载作用
竖向恒载和活载作用下,近塔处主梁承受巨大的轴向压力,有可能成为制约斜拉桥跨径发展的因素。根据文献[1]推导的近似计算公式可得:

从而有:
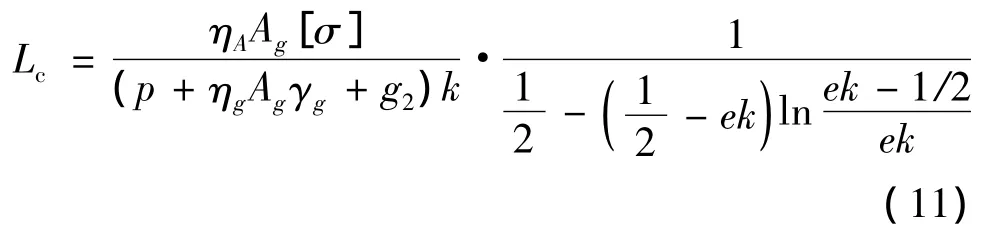
式中:N0为主梁近塔处的最大轴向压力;ηA为近塔处主梁截面面积的增大系数,ηA=1.25;A0,Ag,[σ],γg分别为主梁的近塔处截面面积、平均截面面积、容许应力和容重,Ag=2~5 m2,γg=7.85×104N/m3,对于Q370qD钢主梁,截面容许应力[σ]=200 MPa;ηg为考虑主梁加劲肋等附加作用时的主梁容重增大系数,ηg=1.25;p,g分别为主梁的均布活载和恒载,p=7×104N/m;g2为桥面铺装、栏杆等二期恒载,g2=7×104N/m;k为拉索的梁塔索距比。
斜拉桥极限跨径与主梁平均截面面积之间的关系如图7。
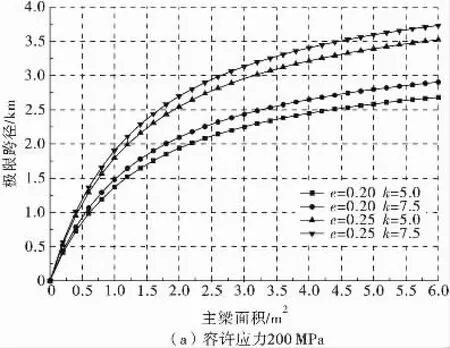
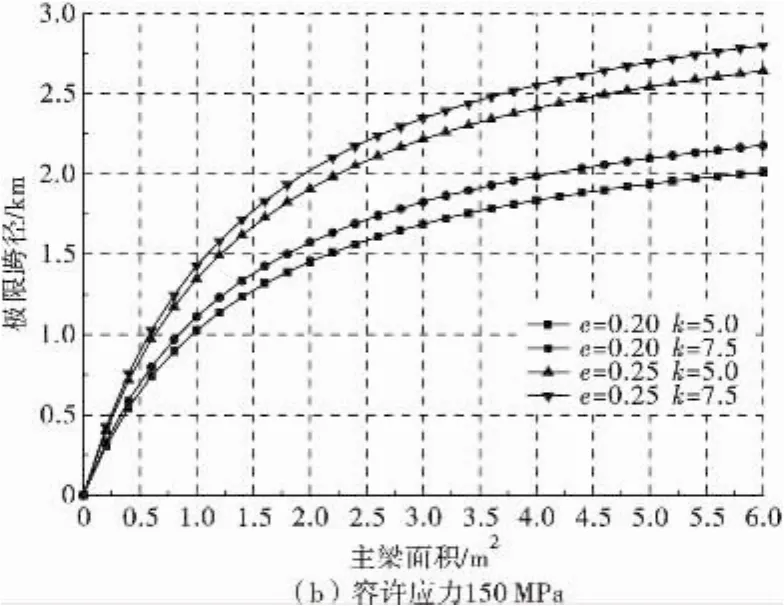
图7 极限跨径与主梁平均截面面积之间的关系Fig.7 Relationship of limitation span and average girder sectional area
由图7可以看出:极限跨径随着主梁面积的增大而增大;当主梁面积一定时,极限跨径随着拉索的梁塔索距比的增大而增大,随着索塔高跨比的增大而增大。当主梁面积小于3.0 m2时,增大面积对提高极限跨径的效果是明显的,但主梁面积大于3.0 m2时,增大面积对提高极限跨径的效果是有限的。当主梁平均截面面积取3.0 m2,梁塔索距比取5.0,索塔高跨比取0.20时,容许应力为200 MPa时,斜拉桥的极限跨径仅为2 251 m。
上述推导过程中未计入恒载、活载对主梁的弯矩作用。考虑上、下缘弯曲应力时,主梁的轴向平均压应力的容许值则降低许多,这里假设考虑弯矩后主梁容许轴向应力取150 MPa,则同等条件下,斜拉桥的极限跨径降低为1 688 m。
恒载、活载组合作用下,影响主梁强度的主要因素有索塔高跨比、主跨跨径、梁塔索距比、主梁容重等。当主梁材料的容许应力一定时,通过增大高跨比、减小塔上索距、增大梁上索距、降低主梁自重等措施,可以有效地提高斜拉桥的极限跨径。采用高强度主梁材料,也可以迅速提高斜拉桥的极限跨径,如主梁采用Q420钢材,其容许应力为220 MPa,则极限跨径可提高1.1倍。
2.2 恒载 +横向极限静阵风作用
根据近似计算公式,横向极限静阵风作用下,近塔处主梁的横向弯矩为:

式中:ξ为主梁的边跨与主跨的跨径比;q为作用在主梁上的横向极限静阵风荷载,根据JTG/T D 60-01—2004《公路桥梁抗风设计规范》,取值如下:

式中:ρ为空气密度,取1.25 kg/m3;Vg为静阵风风速;CH为主梁的阻力系数,当主梁宽高比B∶h>8∶1时,可取1.3,采用斜腹板时可进行折减,此处折减30%,则得CH=0.91;H为主梁的投影高度,宜计入栏杆、防撞护栏以及其它桥梁附属物的实体高度,这里近似的取为主梁的梁高。
截面横向弯曲应力为:

由公式(10)可得恒载作用下的轴向应力为:

各参数取值同上,荷载组合后的截面应力应满足:

参数取值的情况如下:边主跨比ξ取0.45;主梁侧向抗弯惯性矩取为350 m4;主梁选用Q370钢材,在横向极限静阵风作用下,容许应力取302 MPa。
主梁最大应力与主跨跨径之间的关系如图8。

图8 主梁最大应力与主跨跨径之间的关系Fig.8 Relationship of girder maximum stress and main span
从图8可以看出:斜拉桥极限跨径受极限静阵风风速的影响较大,而受索塔高跨比、梁塔索距比、主梁面积的影响较小。斜拉桥极限跨径随着静阵风风速的增加而迅速降低。当主梁平均截面面积取3.0 m2,极限静阵风风速取60 m/s,梁塔索距比取5.0,索塔高跨比取0.20时,斜拉桥的极限跨径仅为1 835 m。
恒载与横向极限静阵风组合作用下,影响主梁强度的主要因素有截面阻力系数、主梁高度、主跨跨径、主梁刚度、索塔高跨比、主梁容重等。改善截面形状、降低梁高可以减小静阵风荷载的大小,从而降低主梁横向挠曲应力,提高斜拉桥的极限跨径。减小索塔的高跨比可以在一定程度上提高斜拉桥的极限跨径。采用轻质高强的主梁材料也可以提高斜拉桥的极限跨径,如主梁采用Q420钢材,其容许应力为346 MPa,则极限跨径可提高到2 005 m。
3 极限跨径
从斜拉索材料强度和主梁材料强度两个方面探讨了当前材料水平和施工水平下全自锚斜拉桥结构体系的极限跨径。为了便于比较,各种因素下的斜拉桥极限跨径列入表1中。表中自锚式斜拉桥极限跨径计算时依据的各种主要参数取值情况如下:恒载集度g=30 t/m,活载集度p=7 t/m,梁上索距λ=10 m,梁塔索距比k=5.0,索塔有效高跨比e=0.2,梁高h=5.0 m,主梁竖向抗弯惯性矩Iy=10 m4,主梁横向抗弯惯性矩Iz=350 m4,设计风速Vd=60 m/s。

表1 自锚式斜拉桥的极限跨径Table 1 Limitation span of self-anchored cable-stayed bridge
斜拉索容许应力[σc]=708 MPa,一般工况下钢主梁容许应力[σ1]=200 MPa,极限静阵风作用下钢主梁容许应力[σ2]=302 MPa。
4 结论
综上所述,可以得出了下面这些有益的结论:
1)横向静阵风作用下的主梁强度是限制斜拉桥跨径增大的主要因素;活载作用下的主梁强度居于次要地位;而斜拉索的强度和效率对斜拉桥极限跨径的影响最小。
2)控制斜拉桥设计的工况首先是横向极限静阵风作用,其次才是活载作用,设计中首先要解决主梁的侧向刚度问题。增大主梁侧向刚度,减小横向静阵风作用下主梁的侧向弯曲应力。
3)主梁的竖向挠度、横向挠度、屈曲稳定性和抗风稳定性也是控制自锚式斜拉桥极限跨径的重要因素,应作进一步的探讨。
(References):
[1] 张杨永.斜拉桥近似计算与结构体系研究[D].上海:同济大学,2010.
Zhang Yangyong.Approximate Calculation and Study of Structural System in Cable-Stayed Bridge[D].Shanghai:Tongji University,2010.
[2] Niles G.Cable Supported Bridges:Concept& Design[M].London:John Wiley& Sons,1997:52-68.
[3] 李国豪.大跨桥梁发展概略[R].上海:同济大学出版社,1987:1-10.
Li Guohao.Outline of Development for Cable-Stayed Bridge[R].Shanghai:Tongji University Press,1987:1-10.
[4] Meier U.Structural tensile elements made of advanced composite materials[J].Structural Engineering International,1999,99(4):281-285.
[5] Muller J M.Very Long Span Bridges:Concepts,Materials and Methods[R].Kobe:IABSE,1998:34-48.
[6] Saul R,林广元.特大跨度的斜拉桥[J].世界桥梁,1991,19(3):78-79.Saul R,Lin Guangyuan.Super long-span cable-stayed bridge[J].World Bridges,1991,19(3):78-79.
[7] 苗家武.超大跨度斜拉桥设计理论研究[D].上海:同济大学,2006.
Miao Jiawu.Study of Design Theory of Super Long-Span Cable-Stayed Bridge[D].Shanghai:Tongji University,2006.
[8] 孙斌.超千米级斜拉桥结构体系研究[D].上海:同济大学,2008.
Sun Bin.Study of Structural System of Ultra-kilometer Cable-Stayed Bridge[D].Shanghai:Tongji University,2008.
[9] 王伯惠.斜拉桥的极限跨径:连载1[J].公路,2002(3):46-53.
Wang Bohui.Extreme span length of cable-stayed bridge:I[J].Highway,2002(3):46-53.
[10]王伯惠.斜拉桥的极限跨径:连载2[J].公路,2002(4):38-48.
Wang Bohui.Extreme span length of cable-stayed bridge:II[J].Highway,2002(4):38-48.
[11]严国敏.试谈四种桥型的最大可能跨度[C]//中国土木工程学会桥梁及结构工程学会:中国土木工程学会桥梁及结构工程学会第九届年会论文集.北京:人民交通出版社,1990:108-104.
Yan Guomin.The Maximum Possible Span of Four Types Bridges[C]//China Civil Engineering Society for Bridge and Structural Engineering Institute:9thAnnual Meeting Proceedings of China Civil Engineering Society for Bridge and Structural Engineering Institute.Beijing:China Communications Press,1990:108-104.
[12]石雪飞,沈炯伟,陈辉.考虑施工可行性的斜拉桥极限跨径研究[J].石家庄铁道学院学报:自然科学版,2009,22(3):5-9.
Shi Xuefei,Shen Jiongwei,Chen Hui.Study on ultimate span of cable-stayed bridge with current construction technique[J].Journal of Shijiazhuang Railway Institute:Natural Science,2009,22(3):5-9.
Limitation Span of Self-Anchored Cable-Stayed Bridge(I)
Zhang Yangyong
(Shanghai Tonghao Civil Engineering Consulting Co.Ltd.,Shanghai 200092,China)
The limitation span of whole self-anchor cable-stayed bridge system is discussed in terms of material strength of stay cable and girder at the current level of material and construction.Research results show that girder strength under transverse limit static gust wind load is the main factor to limit the increase of cable-stayed bridge span;girder strength under live load is secondary factor;stay cable strength and its support efficiency is of little effect on the limitation span of cable-stayed bridge.The primary problem of increasing cable-stayed bridge span is to improve the lateral stiffness of girder.The results provide some reference in concept design for super long span cable-stayed bridge.
cable-stayed bridge;limitation span;limit static gust wind;sag effect;lateral stiffness
U448.27
A
1674-0696(2013)02-0177-06
10.3969/j.issn.1674-0696.2013.02.01
2012-10-30;
2012-12-24
张杨永(1982—),男,江苏淮安人,博士,主要从事桥梁设计理论方面的工作。E-mail:lucky0120@163.com。
